Master Two-Step Equations with Free Worksheets

Mastering two-step equations is a fundamental math skill that students must acquire to progress in their mathematical journey. Solving two-step equations not only strengthens logical thinking but also prepares students for more complex algebraic problems. This comprehensive guide will provide you with strategies, techniques, and free worksheets to master two-step equations effectively. Here's what you need to know to ensure a solid understanding:
Understanding Two-Step Equations

Two-step equations are algebraic expressions where we need to perform two operations to find the value of the variable. These operations typically involve undoing the actions done to the variable, following the opposite of the order of operations.
How to Solve Two-Step Equations

The basic approach to solving two-step equations includes the following steps:
- Isolate the variable term: Use addition or subtraction to remove any constants not attached to the variable.
- Remove the coefficient: Divide or multiply to isolate the variable itself.
🔍 Note: Remember to always keep the equation balanced. Whatever you do to one side, you must do to the other.
Examples

Let's look at a simple example to illustrate the steps:
Consider the equation 2x + 3 = 7
- First, subtract 3 from both sides to isolate the term with 'x':
2x + 3 - 3 = 7 - 3, which simplifies to2x = 4. - Next, divide by 2 to find the value of 'x':
(2x)/2 = 4/2, which gives usx = 2.
Worksheets for Practice

To truly master two-step equations, practice is key. Here are some free, downloadable worksheets tailored to different skill levels:
Beginner Worksheet

This worksheet includes basic two-step equations where the variable has a positive coefficient and constants are on both sides:
Intermediate Worksheet

These equations involve negative coefficients, larger numbers, and some division:
Advanced Worksheet

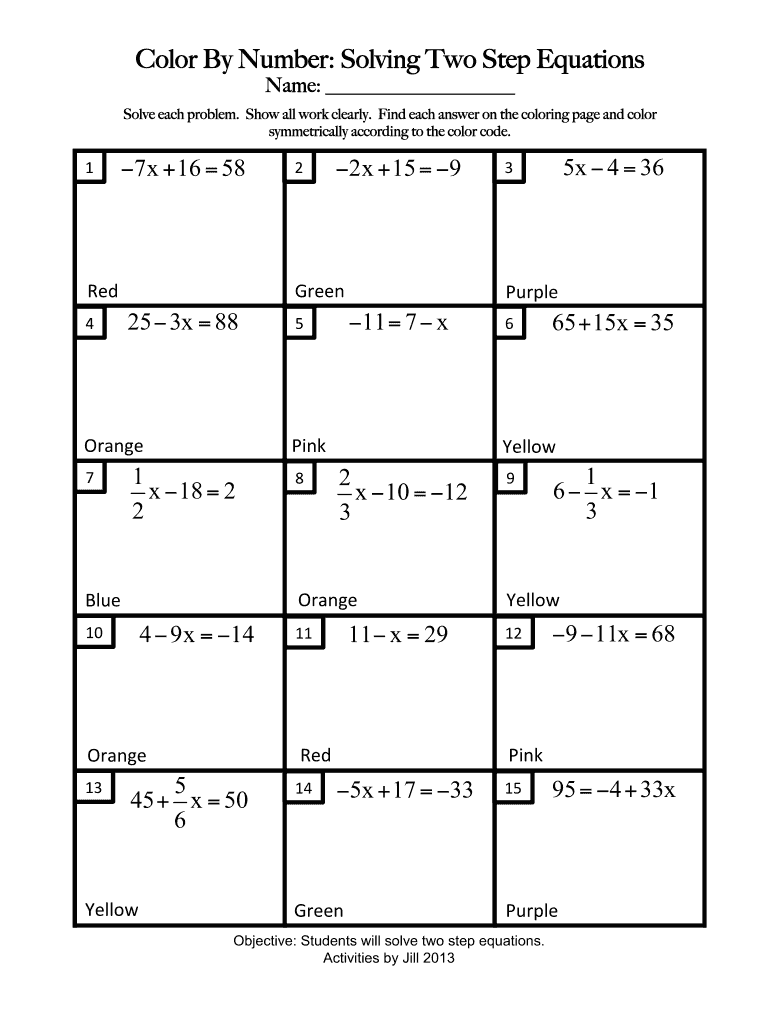
Here, students will face multi-step equations, including distribution and combining like terms:
Tips for Teaching Two-Step Equations

When teaching or learning two-step equations, consider the following tips:
- Use Visual Aids: Tools like algebra tiles can make abstract concepts more tangible.
- Real-World Applications: Connect equations to real-life scenarios to make learning more relatable.
- Incremental Difficulty: Gradually increase the complexity of problems as students become comfortable with the basics.
Assessment and Progress Tracking
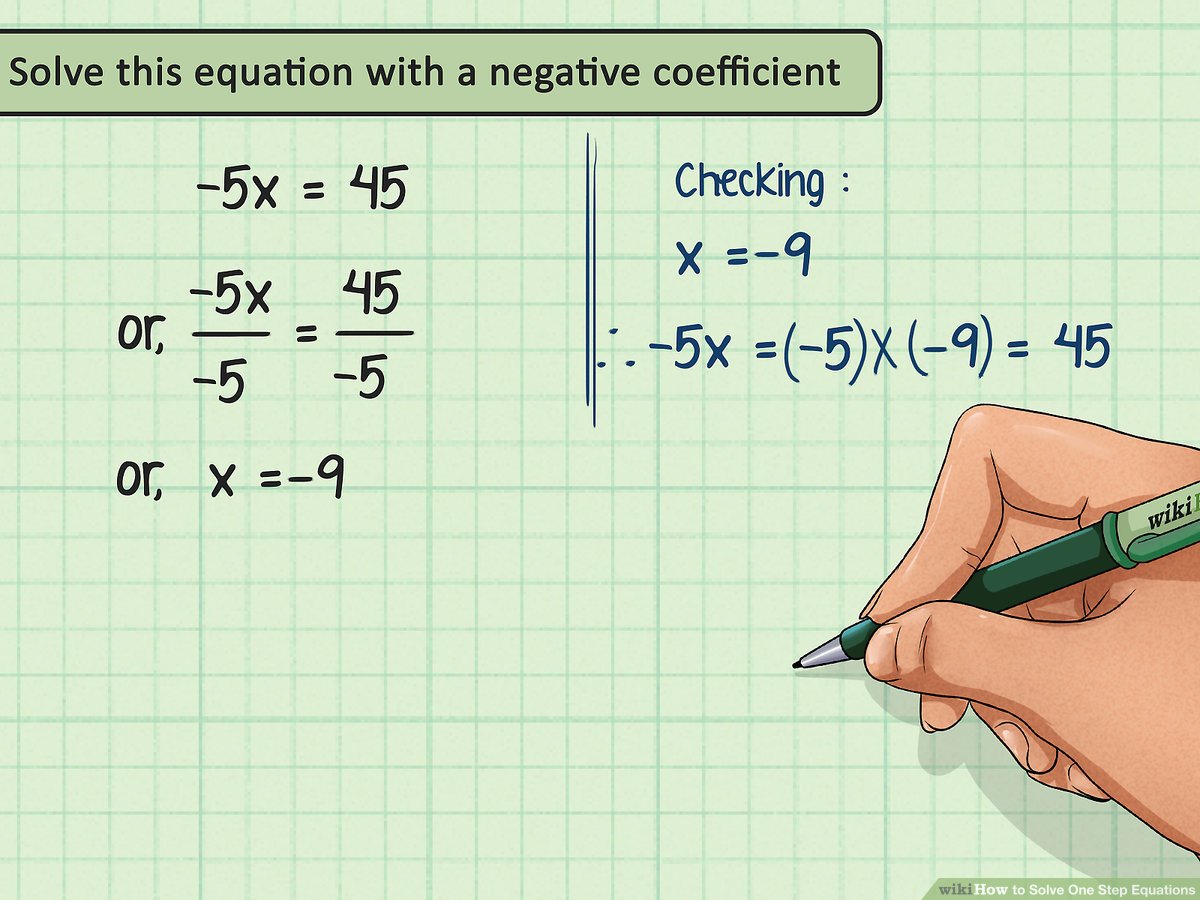
Here’s a table to help track student progress in solving two-step equations:
| Skill Level | Can Solve Equations of Form | Progress Marker |
|---|---|---|
| Beginner | ax + b = c |
Can solve basic two-step equations without negative numbers. |
| Intermediate | ax - b = c |
Can handle negative numbers and division. |
| Advanced | a(bx + c) + d = e |
Able to distribute, combine like terms, and solve multi-step equations. |
💡 Note: Use the progress table to identify where a student needs additional practice or when they are ready to move to the next level.
In Summary

Mastering two-step equations is an essential step in the progression of algebraic education. This guide has provided you with a structured approach to understanding, teaching, and practicing these equations. Remember that consistent practice with the provided free worksheets, coupled with a well-rounded teaching strategy, will significantly enhance students' abilities to solve these equations effectively. As they advance, students will not only conquer two-step equations but will also build the foundation for tackling more complex mathematical problems.
What are two-step equations?

+
Two-step equations are algebraic expressions where two mathematical operations need to be performed to find the value of the variable.
Why do we use two-step equations?

+
They provide a stepping stone from basic arithmetic to more complex algebra, helping students understand the principles of equation balancing and variable manipulation.
How can I make learning two-step equations fun?
+
Introduce interactive activities, games, and real-world problems. Using visual aids like algebra tiles and practical applications can also engage students.



