Transform Your Learning: Translation, Reflection, Rotation Worksheet

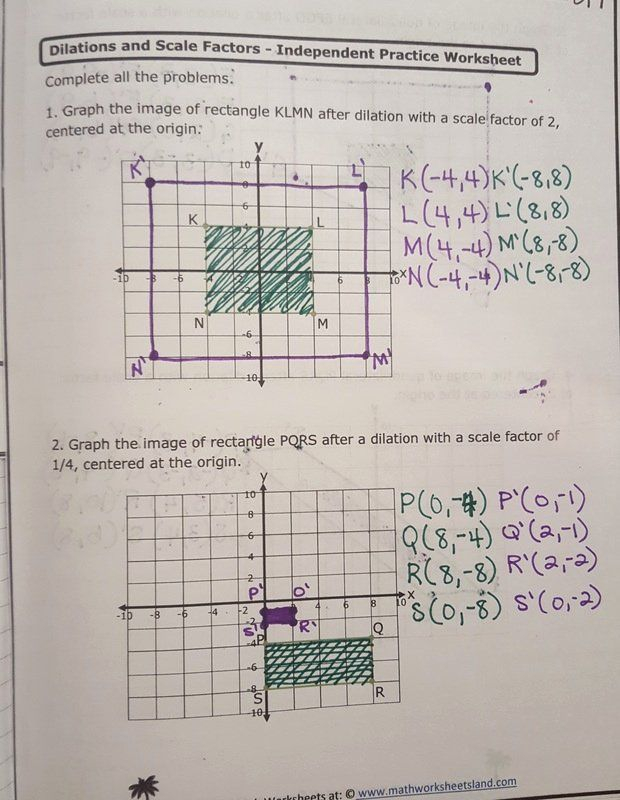
Exploring the concepts of translation, reflection, and rotation can significantly enhance one's understanding of geometry in a practical and engaging way. These transformations are fundamental in both mathematics education and real-world applications, including computer graphics, engineering, and design. Let's delve into how these geometric transformations work, how to use them in a worksheet format, and their implications.
Understanding the Basics of Transformations

Before diving into worksheet creation, understanding the three primary geometric transformations is crucial:
- Translation: This is when you move a shape without rotating or resizing it. Think of sliding a paper across a table.
- Reflection: Reflection involves flipping a figure over a line, often called the line of reflection. It’s like seeing a mirror image.
- Rotation: Here, a figure is turned around a pivot point or axis by a specific angle.
Translation

Translation involves shifting every point of a shape by the same amount in a specified direction. Here’s how it works:
- Identify the starting point of the translation.
- Define the direction and distance (vector) of translation.
- Move each point of the shape by that vector.
For instance, if you’re asked to translate a triangle to the right by 5 units, each vertex of the triangle would move 5 units to the right.
🔄 Note: The angle of translation is always zero, as you’re moving in a straight line.
Reflection

Reflecting an object means every point is as far away from the line of reflection on the other side as it is initially. The steps include:
- Choose the line of reflection.
- For each point, find its perpendicular distance from the line.
- Construct the new point at the same distance on the opposite side of the line.
| Object Point | Line of Reflection | Reflected Point |
|---|---|---|
| (2, 3) | y-axis | (-2, 3) |
| (3, 5) | x-axis | (3, -5) |

Rotation

Rotating an object means turning it around a fixed point, called the center of rotation, by a given angle:
- Identify the center of rotation and the angle of rotation.
- Determine the direction (clockwise or counterclockwise).
- For each point, calculate the new position using trigonometry or construction.
Imagine rotating a square 45 degrees counterclockwise. Each vertex’s coordinates change according to the rotation formula:
- New X = Old X * cos(angle) - Old Y * sin(angle)
- New Y = Old X * sin(angle) + Old Y * cos(angle)
Creating a Transformative Learning Experience

Now, let’s explore how to effectively incorporate these transformations into a worksheet for educational purposes:
Designing the Worksheet

To make learning interactive and hands-on:
- Introduction: Briefly explain each transformation at the beginning.
- Exercises: Provide problems where students must translate, reflect, or rotate shapes given specific instructions.
- Interactive Elements: Include cutouts or diagrams where students can physically manipulate shapes.
- Step-by-Step Examples: Show worked examples to guide students through the process.
- Real-world Scenarios: Relate transformations to real-life examples like floor tiling, flags, or game design.
Here's an example structure:
Section: Translation
- Plot the following points: (0,0), (3,0), (3,3), (0,3). Now translate this square 5 units to the right.
Section: Reflection
- Reflect the triangle with vertices at (1,4), (5,4), (3,7) over the line y = 2.
Section: Rotation
- Rotate a point (2,2) 90 degrees clockwise around the origin.
Maximizing Educational Impact

While creating the worksheet, consider the following:
- Difficulty Gradation: Start with simpler problems and increase complexity.
- Feedback Mechanisms: Include space for students to show their work and check their answers.
- Interdisciplinary Learning: Explore connections with art, physics, or technology.
- Interactive Tools: Suggest using graph paper or digital tools to visualize transformations.
In summary, designing a worksheet around translation, reflection, and rotation not only reinforces mathematical concepts but also introduces students to geometric thinking in a tangible manner. It encourages analytical thinking, spatial awareness, and can be tailored to suit different learning styles and levels of proficiency.
How do I know which direction to rotate an object?

+
Positive angles denote counterclockwise rotation, while negative angles denote clockwise rotation. It’s also determined by the coordinate system used; the right-hand rule can help in 3D rotations.
What real-world application does reflection have?
+
Reflection is used in optics, architecture (symmetry), and computer graphics to simulate mirrors or water reflections. It also appears in music theory when considering inverted chords.
Can I use an app to perform these transformations?

+
Yes, several educational apps and software like GeoGebra or Desmos allow you to explore and perform these transformations visually and interactively.