5 Ways to Master Dilations and Scale Factors
Understanding the Basics of Dilations
Dilations are a fundamental concept in geometry that involve resizing figures through scale factors. Whether you're a student grappling with transformations or a professional using them in design or engineering, mastering dilations can significantly enhance your understanding of spatial relationships. Let's dive into how you can master dilations and scale factors effectively.

1. Grasp the Concept of Scale Factor

At the heart of dilation is the scale factor, a ratio that determines how much each point of the original figure is moved away from (for enlargement) or toward (for reduction) a fixed center. Here's how to understand and use it:
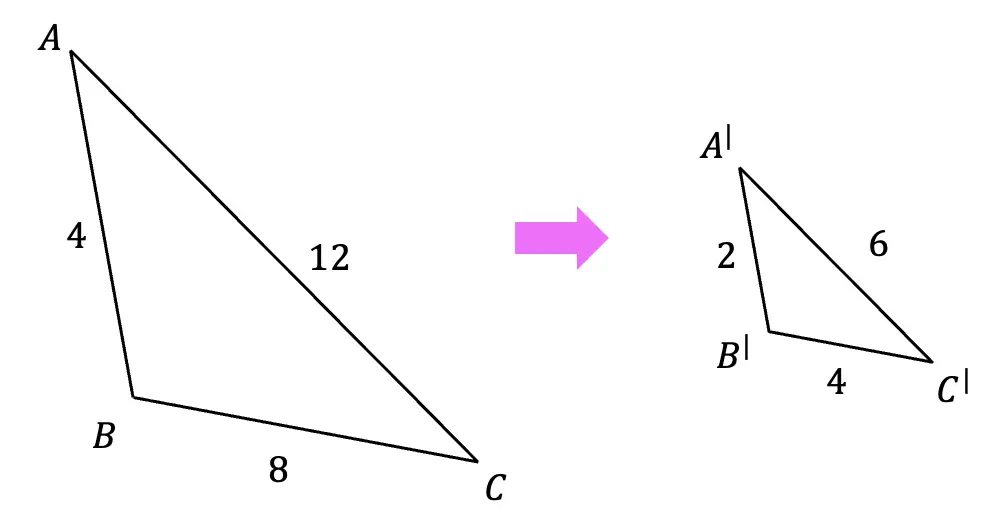
- Enlargement: If the scale factor is greater than 1 (e.g., 2 or 3), the figure is enlarged. For example, if a triangle's sides are multiplied by a scale factor of 2, each side will be twice as long.
- Reduction: If the scale factor is less than 1 (e.g., 0.5 or 1/3), the figure is reduced in size. A triangle with sides scaled by 0.5 will have each side half the original length.
The scale factor must be applied uniformly in all directions. Here are key points:
- The distance from the center of dilation to any point on the original figure is multiplied by the scale factor to determine the corresponding point on the new figure.
- Parallel lines remain parallel after dilation, and corresponding angles remain equal.
2. Practice with Simple Shapes

Begin with basic shapes to get the hang of dilations:
- Start with a simple shape like a square or triangle. Mark the center of dilation, then multiply each side's length by the scale factor. Remember, the center point remains fixed.
- Experiment with different scale factors. Try both enlargements and reductions to understand how the shape changes.
💡 Note: Drawing accurate dilations by hand helps in visualizing the process, but using software like GeoGebra can provide instant visual feedback and make complex calculations easier.
3. Use Real-Life Examples
Connecting mathematical concepts to real-world applications can make learning more engaging:
- Photography: When resizing images in photo editing software, you are using dilation. Notice how the image's dimensions are changed with a scale factor.
- Map Scaling: Maps often use dilations to represent larger areas in a smaller space. Understanding how the scale factor affects the map's size and readability is crucial for geographers and urban planners.
- Architectural Models: Architects use dilations to create scale models of buildings. The model's size must represent the real structure accurately, often using scale factors like 1:50 or 1:100.
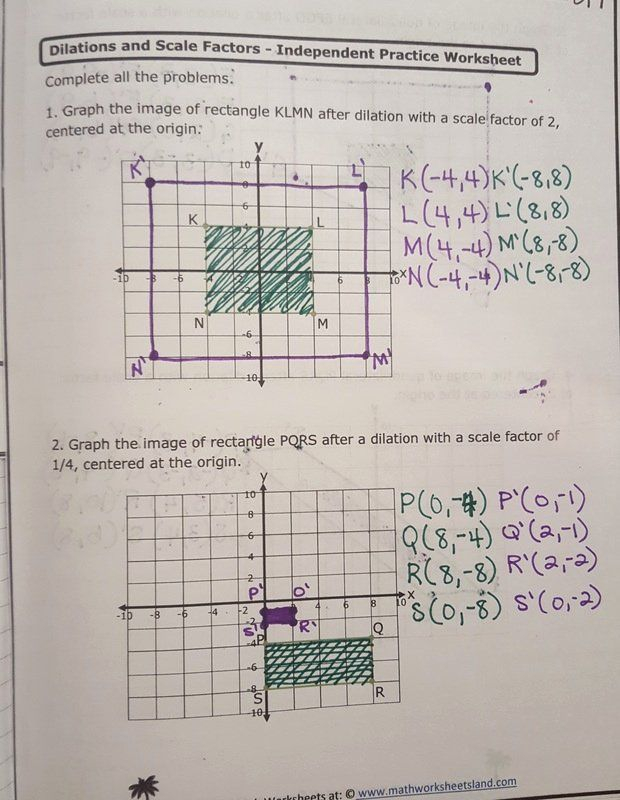
4. Explore Coordinate Geometry
When working with dilations in a coordinate plane, the process becomes more precise:
- If the center of dilation is not at the origin, translate the figure so the center is at (0,0). Then apply the scale factor to the x and y coordinates of each point. Finally, translate the figure back to its original position relative to the center.
- Use formulas like (x', y') = k(x, y), where k is the scale factor, to find new coordinates for points.
Here's a simple table showing dilation from point (2, 4) with scale factor 3:
| Original Point | Scale Factor | Dilated Point |
|---|---|---|
| (2, 4) | 3 | (6, 12) |

🔍 Note: When dealing with negative scale factors, dilation creates a mirror image of the figure across the center of dilation.
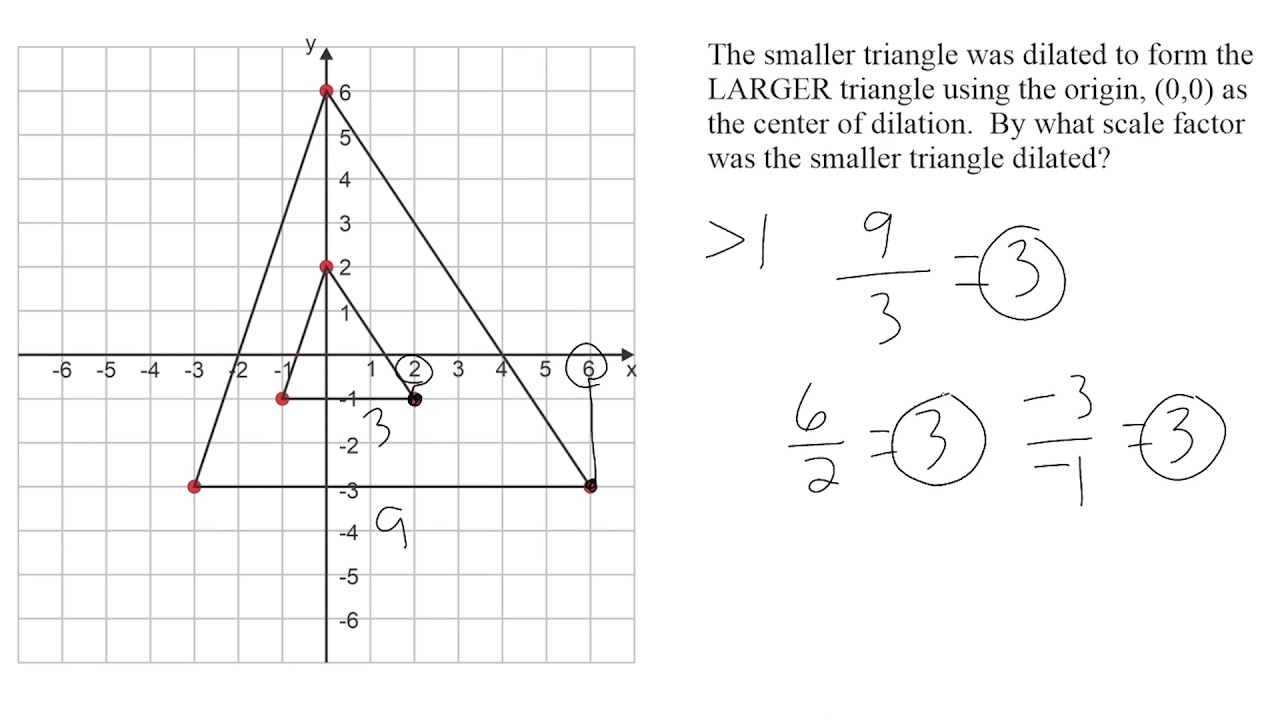
5. Solve Problems and Apply Concepts

To master dilations, engage in problem-solving:
- Find the center of dilation: Given two similar figures, determine the center of dilation and the scale factor. Use the properties that corresponding lines are parallel and ratios of distances from the center are equal.
- Proofs involving dilations: Understand and prove properties like congruent angles and proportional sides in similar figures.
- Transformation matrices: Learn how matrices can represent dilations, which is particularly useful in computer graphics and linear algebra.
In wrapping up our exploration of mastering dilations and scale factors, it’s clear that this skill not only deepens your understanding of geometry but also has practical applications in various fields. By grasping the scale factor, practicing with simple shapes, relating concepts to real-life examples, exploring coordinate geometry, and engaging in problem-solving, you can elevate your proficiency in this essential geometric transformation. Remember, the beauty of mathematics lies in its ability to represent and explain the world around us through patterns and numbers.
What is the difference between dilation and translation?

+
Translation moves every point in a figure the same distance in the same direction, maintaining its size and orientation. Dilation, however, changes the size of the figure while keeping the shape proportionate through a scale factor.
How do you find the center of dilation?

+
When you have two similar figures, draw lines connecting corresponding points. The lines should intersect at the center of dilation. Use the ratio of the distances from the center to corresponding points to find the scale factor.
Can dilations produce reflections?

+
Yes, using a negative scale factor results in a dilation that also reflects the figure across the center of dilation, producing a mirror image.