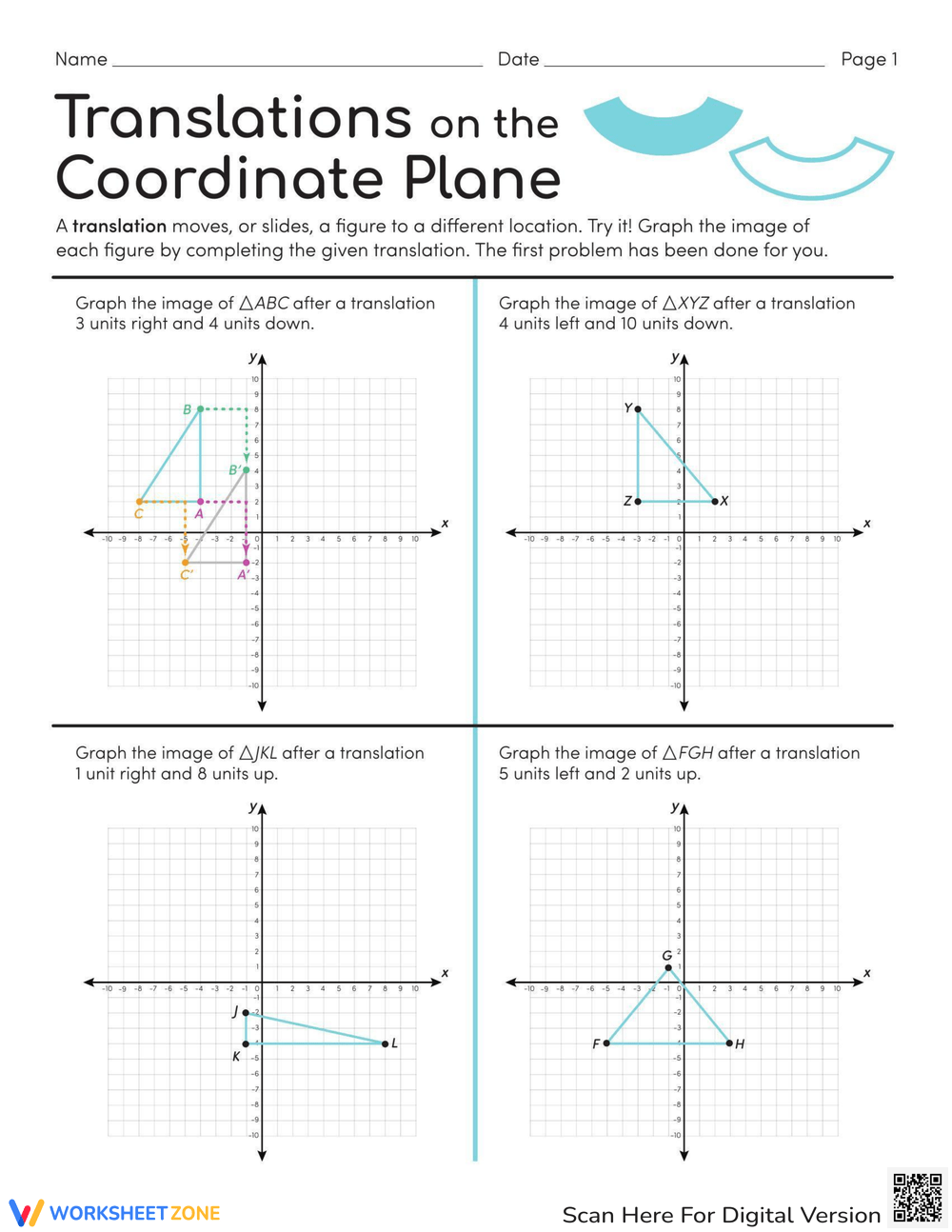
Master Geometry Translations with Our Fun Worksheet
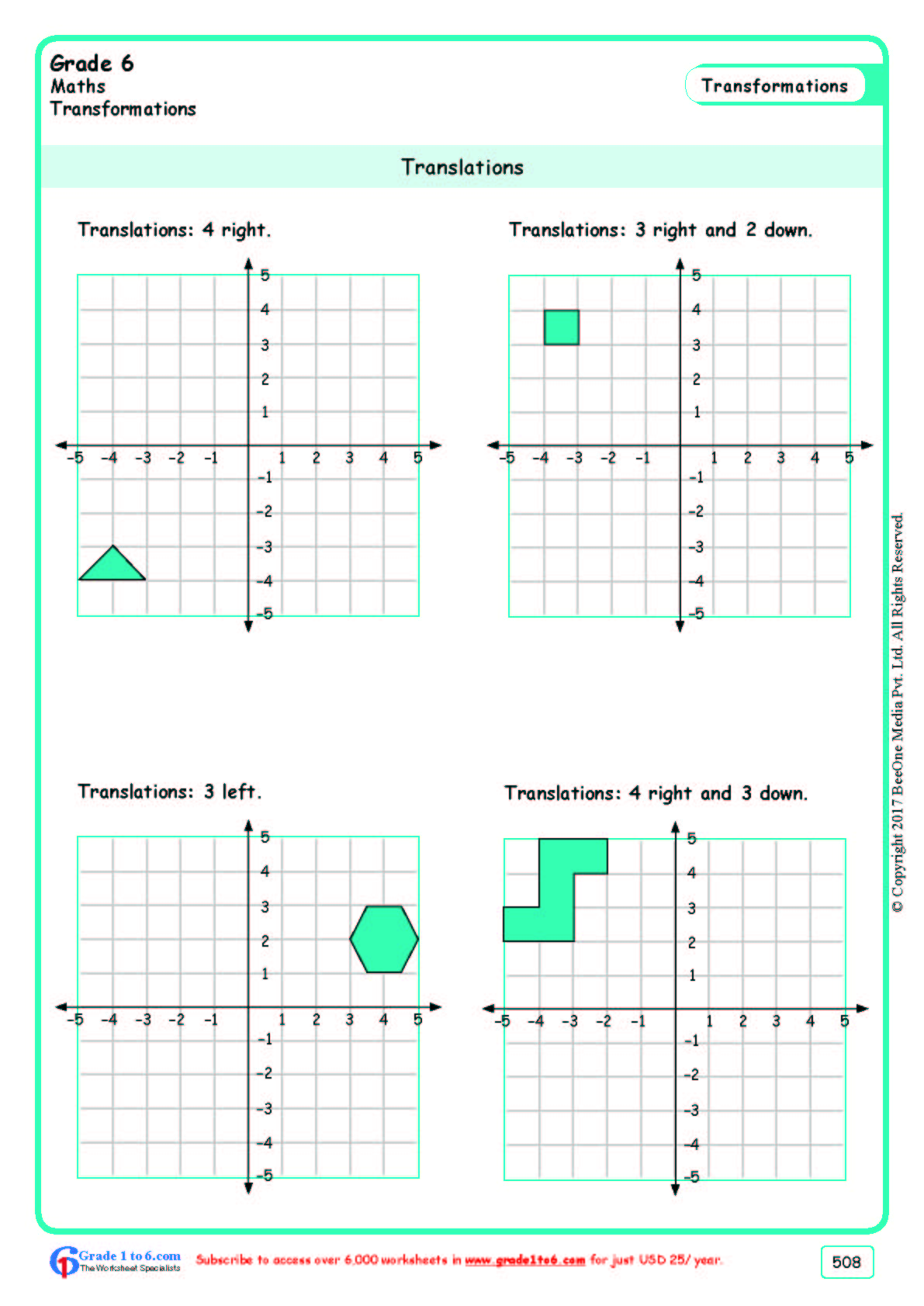
Understanding Geometry Translations
Translating shapes in geometry might seem daunting at first, but with the right tools and a fun worksheet, it can become an engaging and straightforward task. Translation, in geometry, refers to the process of moving a shape from one position to another without altering its size or orientation. Today, we’ll delve into this concept, providing you with practical examples, tips, and an interactive worksheet to make learning translations in geometry as fun as it can be.
Geometry translation involves the transformation of figures on a coordinate plane, which means moving every point of the figure the same distance and in the same direction. Here's how you can visualize this process:
- Identify Points: First, identify key points on the shape you wish to translate. For instance, if you are moving a triangle, note the coordinates of its vertices.
- Determine Movement: Decide how much you want to move each point horizontally (left or right) and vertically (up or down).
- Apply Translation: Add or subtract these distances from the original coordinates to find the new position of the shape. If you're moving right or up, you add; if left or down, you subtract.
Practical Examples of Geometry Translations
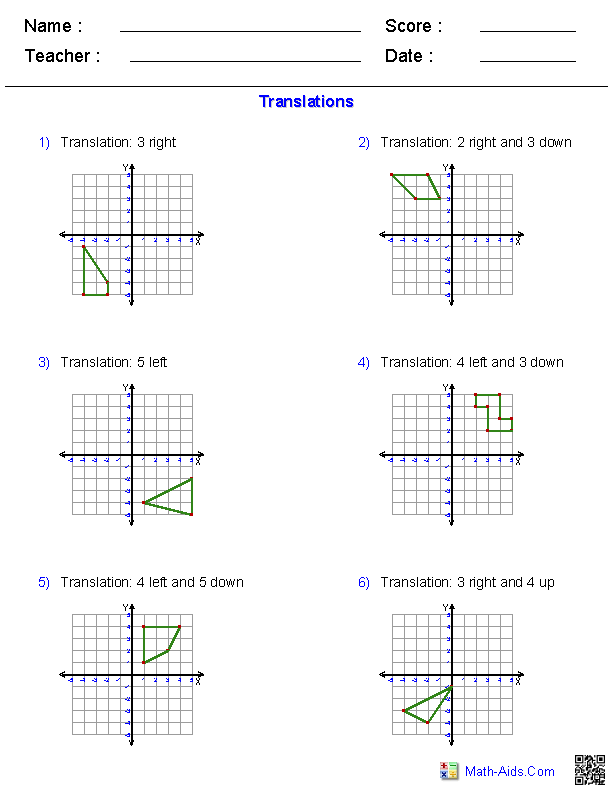
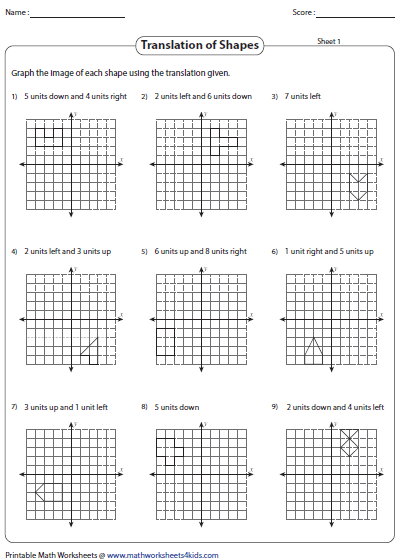
Let’s look at some practical examples to understand how translations work in the real world:
Example 1: Moving a Rectangle


- Original vertices: (1, 2), (3, 2), (3, 4), (1, 4).
- Move 2 units to the right and 1 unit down.
- New vertices: (1+2=3, 2-1=1), (3+2=5, 2-1=1), (3+2=5, 4-1=3), (1+2=3, 4-1=3).
Example 2: Translating a Triangle
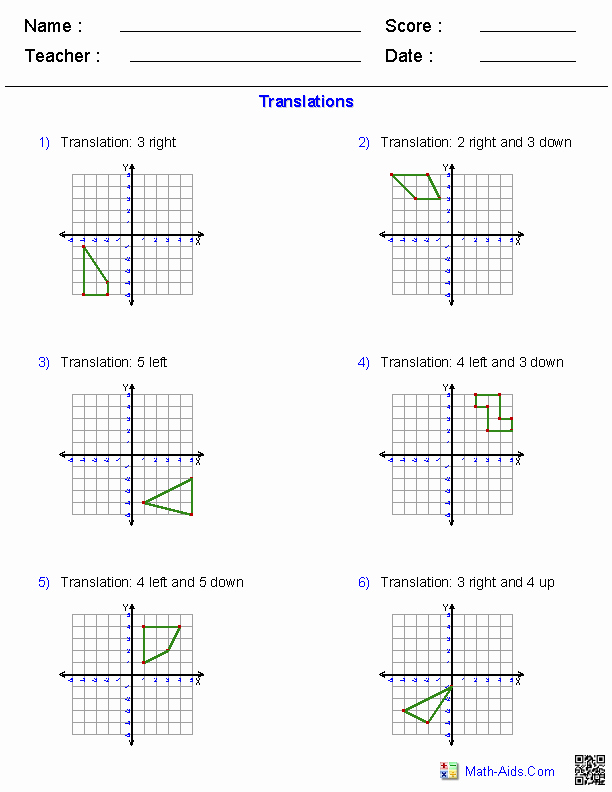
- Original vertices: (0,0), (3,0), (3,4).
- Move 1 unit to the left and 3 units up.
- New vertices: (0-1=-1, 0+3=3), (3-1=2, 0+3=3), (3-1=2, 4+3=7).
Your Fun Geometry Translation Worksheet

To truly master geometry translations, here’s a fun worksheet you can use:
| Figure | Original Points | Translation | New Points |
|---|---|---|---|
| Rectangle | (1,1), (5,1), (5,4), (1,4) | Move 3 units right, 2 units up | (?, ?), (?, ?), (?, ?), (?, ?) |
| Triangle | (2,3), (2,5), (6,5) | Move 1 unit left, 4 units down | (?, ?), (?, ?), (?, ?) |
| Circle (Center) | (-1,0) | Move 2 units right, 1 unit up | (?, ?) |

✍️ Note: You can make translations easier by using graph paper to plot the original points and then move them according to the given instructions.
Tips for Understanding Translations

Here are some tips to help you master the concept of translations:
- Use Graph Paper: Graph paper helps visualize the movement of points more clearly.
- Check Your Work: After translating a shape, check that all points have been moved the same distance and in the same direction.
- Interactive Tools: Use online geometry tools or mobile apps designed for educational purposes to explore translations interactively.
Further Applications of Geometry Translations

Geometry isn’t just for solving abstract problems; it’s pivotal in various real-world applications:
Design and Architecture

- Architects use translations to design buildings and spaces, ensuring symmetry and alignment in structures.
- Artists apply translations to create patterns or to position elements in their compositions.
Video Game Design
- Characters and objects in video games are often animated using translations to simulate movements like running, jumping, or sliding.
Engineering

- In robotics, translations are used to program the motion of robotic arms or vehicles, ensuring precise movement.
- CAD software uses translations to manipulate 3D models for design purposes.
Summing Up
Geometry translations are not only a fundamental aspect of mathematics but also have wide applications in the real world. By engaging with fun exercises and examples, you can develop a better understanding of how translations work, which will benefit you in various fields beyond just math. Whether you’re designing a building, developing a video game, or solving complex engineering problems, the ability to translate shapes accurately will serve you well. Keep practicing with interactive tools, and don’t forget to enjoy the journey of mastering this fascinating aspect of geometry.
What is geometry translation?

+
Geometry translation is the process of moving a shape or figure from one place to another on a plane without changing its size, shape, or orientation. Every point of the shape moves the same distance and in the same direction.
Can translation affect the shape’s orientation?

+
No, translations only move the shape. The shape remains the same in terms of size and orientation; only its position changes.
How can I ensure I am translating a shape correctly?

+
Use graph paper to plot the original points of your shape and move them according to the translation vector (direction and distance). Check that all points have been moved equally in the same direction to ensure accuracy.



