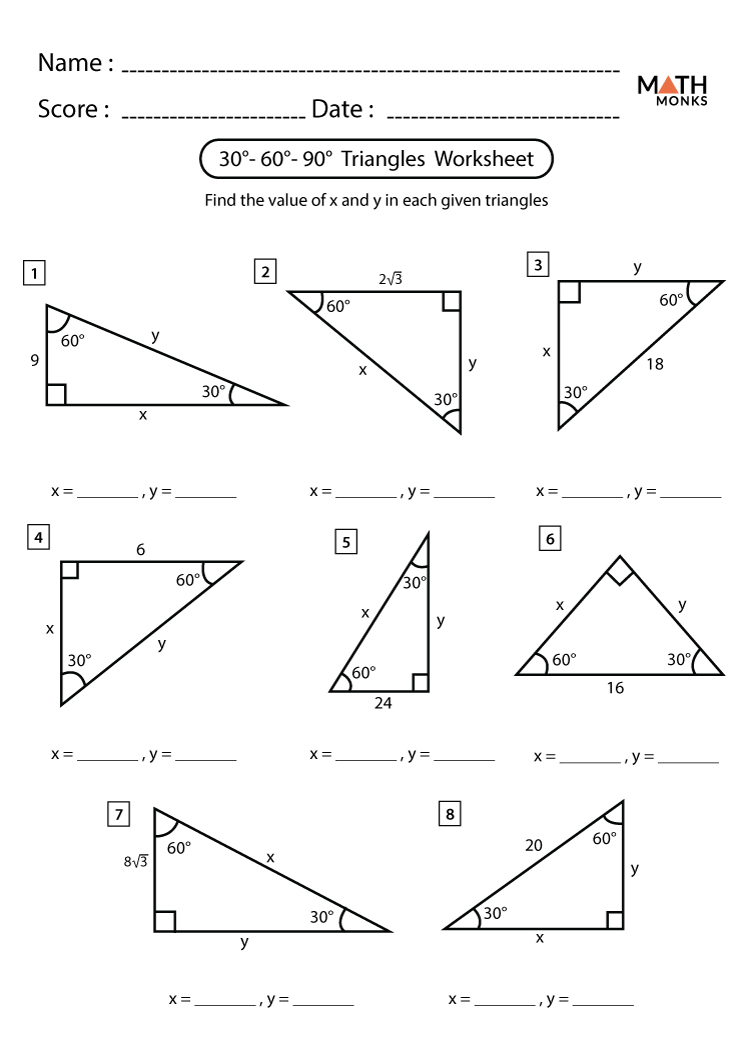
Master the Distance Formula with Our Engaging Worksheet

Learning mathematical concepts can sometimes feel overwhelming, but with the right approach, it can become a rewarding journey. The Distance Formula is a prime example of a mathematical tool that can seem daunting at first but, once mastered, offers a gateway to numerous applications in geometry, physics, and beyond. Let's dive into understanding this formula through an engaging worksheet that simplifies the learning process.
Understanding the Distance Formula

The Distance Formula is used to calculate the distance between two points in a two-dimensional coordinate system. For points (x_1, y_1) and (x_2, y_2) , the formula is given by:
d = √[(x2 - x1)² + (y2 - y1)²]
💡 Note: The square root symbol (√) signifies the distance is always a non-negative value.
This formula originates from the Pythagorean Theorem, where the line joining two points forms the hypotenuse of a right triangle. Understanding this geometric foundation helps in visualizing how the formula applies.
Step-by-Step Worksheet on the Distance Formula

Let's break down the distance formula through a series of exercises. Here's how you can engage with this formula:
1. Conceptual Understanding

- What is the concept of distance in the context of the coordinate plane?
- How does the Distance Formula relate to the Pythagorean Theorem?
📝 Note: Sketching a right triangle on coordinate axes can help visualize the relationship.
2. Basic Application

Calculate the distance between the following pairs of points:
| Point A | Point B | Distance |
|---|---|---|
| (2, 3) | (5, 7) | |
| (-1, 2) | (4, -3) | |
| (0, 0) | (1, 1) |

3. Practical Application

- Find the Perimeter: Given vertices of a triangle A(-2, 4), B(5, 3), C(1, -1), calculate the perimeter.
- Verify Midpoint: If a line segment has endpoints at (4, 6) and (2, -2), check if the midpoint formula gives a point on the segment's line.
4. Problem Solving
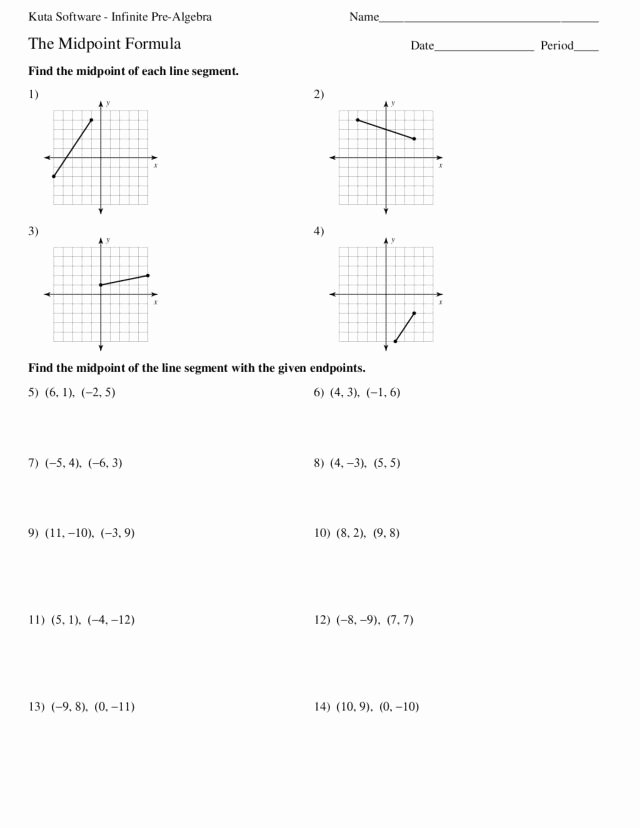
Work through problems that require you to apply the Distance Formula in diverse scenarios:
- Is the triangle with vertices at (-2, 4), (3, -5), and (8, 0) a right triangle?
- Find the distance from the origin to the point where the line y = 2x intersects the y-axis.
By engaging with these exercises, you'll not only grasp how to apply the Distance Formula but also how it fits into the larger mathematical ecosystem. This understanding enhances problem-solving skills, making you adept at tackling complex mathematical challenges.
In mastering the Distance Formula, it's clear how it serves as a fundamental tool for quantifying distances in a two-dimensional space. This knowledge not only boosts your geometric problem-solving capabilities but also prepares you for more advanced mathematical explorations. From calculating distances to verifying shapes, the Distance Formula opens up a world where numbers tell stories of space and geometry.
Why is the Distance Formula important in mathematics?

+
The Distance Formula allows us to calculate distances in two-dimensional space, essential for numerous mathematical and physical applications including geometry, physics, and engineering.
Can the Distance Formula be used in higher dimensions?

+
Yes, while the formula given here is for 2D space, it can be extended to higher dimensions. For 3D, the formula includes z-coordinates, and for n-dimensional space, it’s generalized further.
How does the Distance Formula relate to the Pythagorean Theorem?

+
The Distance Formula is essentially an application of the Pythagorean Theorem, where the difference in x and y coordinates forms the legs of the triangle, and the distance is the hypotenuse.