Inelastic Collisions: Simplified Answers for Students

Understanding inelastic collisions is a foundational concept in physics that often confuses students due to its nuanced implications and the variety of real-world scenarios it applies to. In this comprehensive blog post, we'll demystify inelastic collisions by breaking down the concepts, offering illustrative examples, and addressing common pitfalls with clear explanations.
What is an Inelastic Collision?

An inelastic collision occurs when two objects collide, and their total kinetic energy after the collision is less than their total kinetic energy before the collision. Here are the key points:
- Conservation of Momentum: The momentum of the system is always conserved, regardless of whether the collision is elastic or inelastic.
- Loss of Kinetic Energy: Some of the initial kinetic energy is transformed into other forms of energy like heat, sound, or deformation of objects.
- Types of Inelastic Collisions: Completely inelastic collisions result in the objects sticking together post-collision, while partially inelastic collisions involve some sticking but not complete merging.
🔎 Note: In real-world applications, few collisions are truly completely inelastic; most have a degree of partial inelasticity.
Real-Life Examples

To better grasp the concept, let’s look at some real-life examples:
- Car Accidents: When two cars collide, they often stick together or deform, reducing their kinetic energy. This is an example of a partially or completely inelastic collision.
- Sports: In sports like football, the tackling between players can result in an inelastic collision where momentum is transferred but not all kinetic energy.
Mathematical Representation
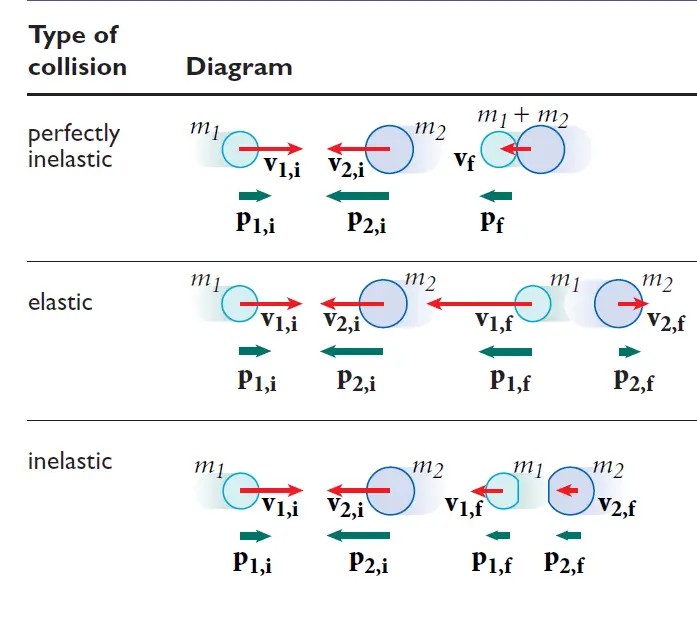
The equations governing inelastic collisions are derived from the principles of conservation of momentum and kinetic energy:
Conservation of Momentum: [ m1v{1i} + m2v{2i} = (m_1 + m_2)v_f ]
Loss of Kinetic Energy: [ \frac{1}{2}m1v{1i}^2 + \frac{1}{2}m2v{2i}^2 > \frac{1}{2}(m_1 + m_2)v_f^2 ]
| Symbol | Meaning |
|---|---|
| m1, m2 | Masses of the colliding objects |
| v1i, v2i | Initial velocities of the objects |
| vf | Final velocity of the system after the collision |

🧐 Note: These equations assume one-dimensional collisions for simplicity, but the principles extend to multiple dimensions with more complex vector calculus.
Classroom Experiment

Setting up a basic experiment to visualize inelastic collisions can be an excellent learning aid:
- Materials: Two masses, a track to minimize friction, and a way to measure velocities.
- Procedure:
- Start one mass moving on the track and keep the other stationary.
- Upon collision, measure the combined velocity of the masses.
- Compare the total initial momentum with the final momentum to verify conservation.
✅ Note: Use a smart phone’s slow-motion camera to capture the collision for a more accurate analysis.
Common Student Misconceptions

Here are a few misconceptions students often have about inelastic collisions:
- Momentum vs. Kinetic Energy: Students confuse momentum conservation with kinetic energy conservation. Remember, in inelastic collisions, momentum is conserved, but kinetic energy is not.
- Elastic vs. Inelastic: Students might assume a collision where the objects bounce back is inelastic because they think of “elastic” as returning to original form. An inelastic collision can still involve bouncing; the key is the loss of kinetic energy.
In summary, understanding inelastic collisions involves recognizing the conservation of momentum, the transformation of kinetic energy into other forms of energy, and how these principles apply in real-life scenarios. From car accidents to sports, the impact of inelastic collisions is widespread. By breaking down the concepts into digestible explanations and experimenting with simple classroom setups, students can gain a clear understanding of this physical phenomenon. Through practical examples, mathematical representation, and addressing common misconceptions, we've aimed to provide students with the tools to navigate and appreciate the world of inelastic collisions with greater confidence and understanding.
What’s the main difference between elastic and inelastic collisions?

+
The primary difference lies in the conservation of kinetic energy. In elastic collisions, both momentum and kinetic energy are conserved. In inelastic collisions, only momentum is conserved while some kinetic energy is transformed into other forms of energy.
Can kinetic energy increase in an inelastic collision?

+
In an inelastic collision, the total kinetic energy of the system decreases because some energy is converted into other forms like heat, sound, or deformation. However, kinetic energy can redistribute among the colliding objects.
How do you calculate the final velocity in an inelastic collision?

+
You use the conservation of momentum. If ( m_1 ) and ( m2 ) are the masses of the objects, and ( v{1i} ) and ( v_{2i} ) are their initial velocities, then the final combined velocity ( v_f ) is calculated as: [ v_f = \frac{m1v{1i} + m2v{2i}}{m_1 + m_2} ]



