30-60-90 Triangle Worksheet: 5 Proven Answers
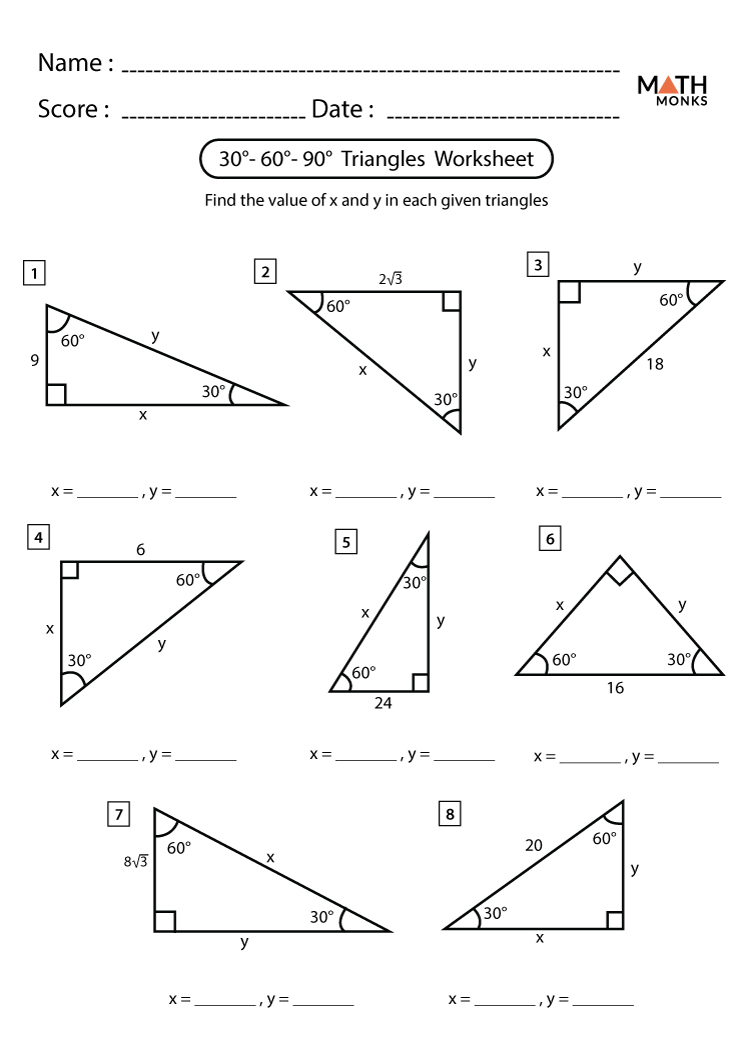
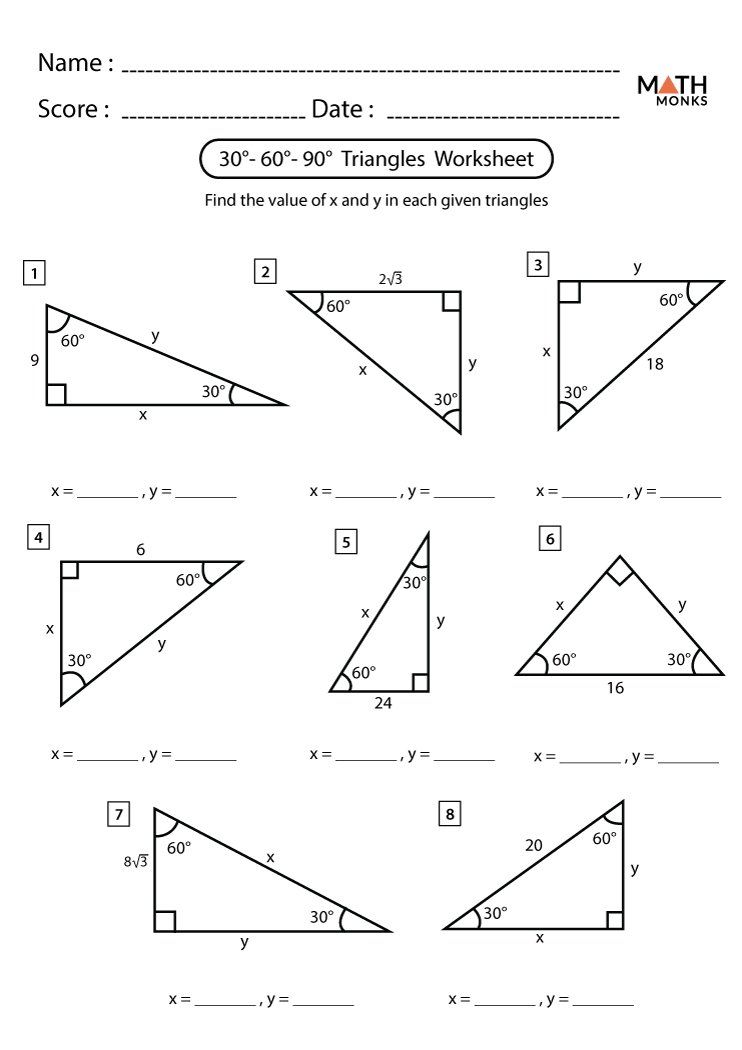
Understanding the intricacies of the 30-60-90 triangle can significantly enhance your geometry skills, particularly when you're preparing for competitive exams, dealing with trigonometry, or simply aiming to improve your math proficiency. In this comprehensive guide, we'll dive deep into the specifics of this special triangle, explore practical examples, and provide proven answers to common problems associated with 30-60-90 triangles.
Understanding the 30-60-90 Triangle

A 30-60-90 triangle is a type of right triangle where the angles are 30 degrees, 60 degrees, and 90 degrees. Here’s what makes it unique:
- The shortest side, opposite the smallest angle (30°), is always half the length of the hypotenuse.
- The side opposite the 60° angle is √3 times the length of the shortest side.
Basic Rules of a 30-60-90 Triangle

| Angle | Side | Length |
|---|---|---|
| 30° | Shortest side | x |
| 60° | Middle side | x√3 |
| 90° | Hypotenuse | 2x |
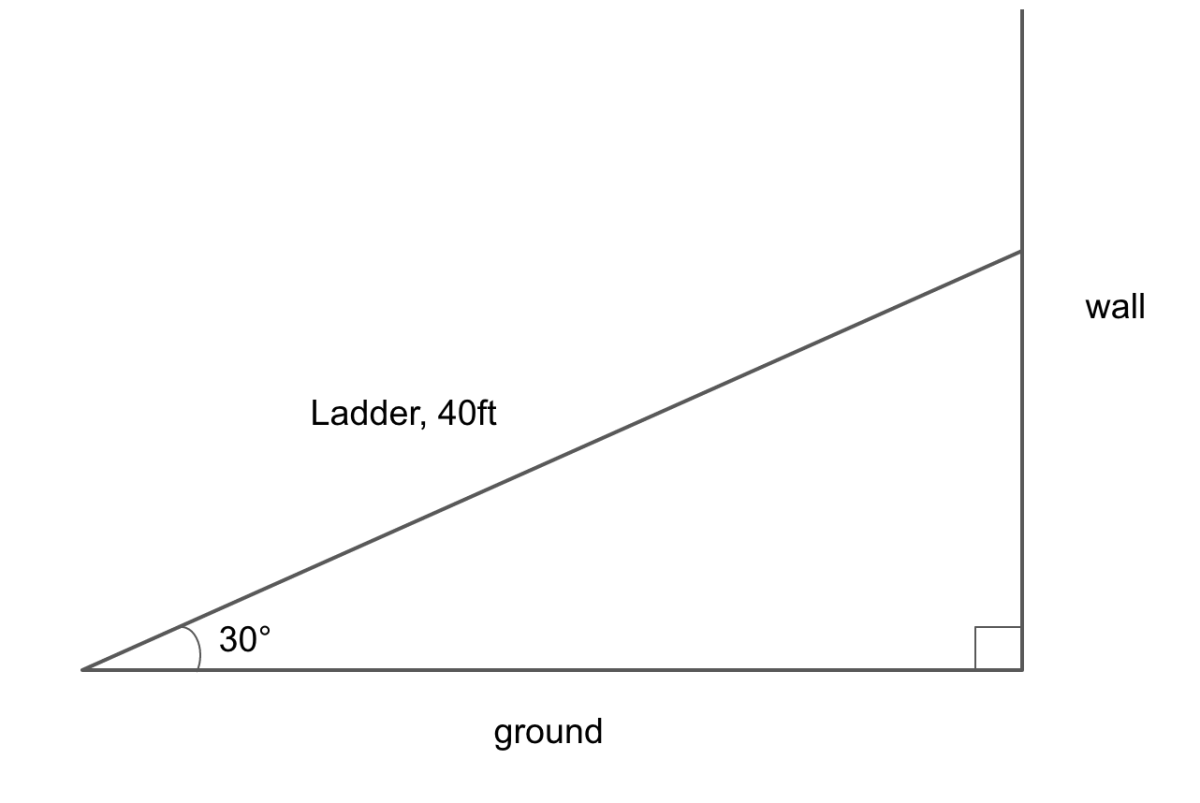
🔑 Note: The variable 'x' represents the length of the side opposite the 30° angle. Always start with this known quantity when solving for other sides.
Proven Answers: Solving Common Problems

Let’s walk through five scenarios where understanding 30-60-90 triangles is crucial:
1. Finding the Length of the Hypotenuse

If the shortest side (opposite the 30° angle) is 5 cm:
- Hypotenuse = 2 x 5 = 10 cm
2. Determining the 60° Side

If the shortest side (opposite the 30° angle) is 4 cm:
- Side opposite 60° = 4 x √3 = 4√3 cm
3. Using Known Hypotenuse to Find Shortest Side

If the hypotenuse is 16 cm:
- Shortest side = 16 / 2 = 8 cm
4. Finding the Area of a 30-60-90 Triangle
If the shortest side is 6 cm:
- Base (60° side) = 6√3 cm
- Height (shortest side) = 6 cm
- Area = (1⁄2) * base * height = (1⁄2) * 6√3 * 6 = 18√3 cm²
5. Calculating the Perimeter

If the shortest side is 5 cm:
- Shortest side = 5 cm
- Side opposite 60° = 5√3 cm
- Hypotenuse = 10 cm
- Perimeter = 5 + 5√3 + 10 = 15 + 5√3 cm
📐 Note: When dealing with irrational numbers like √3, it's often useful to leave them in their radical form for simplicity in further calculations or when exact precision is needed.
In summary, mastering the 30-60-90 triangle involves understanding the relationships between its sides and angles. From finding hypotenuse lengths to calculating areas and perimeters, these rules provide a solid foundation for tackling geometric and trigonometric problems. Applying these principles in real-world scenarios or math competitions can give you a significant advantage, making the study of these special triangles invaluable for any student of mathematics.
What is the importance of knowing the properties of a 30-60-90 triangle?

+
Knowing the properties of a 30-60-90 triangle simplifies the solving of many geometry and trigonometry problems. It allows for quick calculations of sides, area, and related properties without having to resort to complex trigonometric identities.
Can these principles apply to other triangles?

+
While the exact ratios of the 30-60-90 triangle are unique, understanding how specific triangles behave can provide insights into solving problems with other types of triangles, especially when they can be broken down into components involving right angles.
What are some common mistakes when dealing with 30-60-90 triangles?

+
Common mistakes include:
- Confusing the lengths of sides based on incorrect angle assignments.
- Not recognizing that the hypotenuse is twice the shortest side.
- Forgetting to use √3 when calculating the side opposite the 60° angle.



