Geometry often presents students and enthusiasts with various shapes and configurations, each possessing unique properties and applications. Among these, the 30-60-90 triangle stands out as a special type of right triangle with fixed angle measures and sides in a specific ratio. This article aims to unravel the mysteries of 30-60-90 triangles, offering insights into their properties, practical applications, and strategies for solving related problems.
Understanding 30-60-90 Triangles
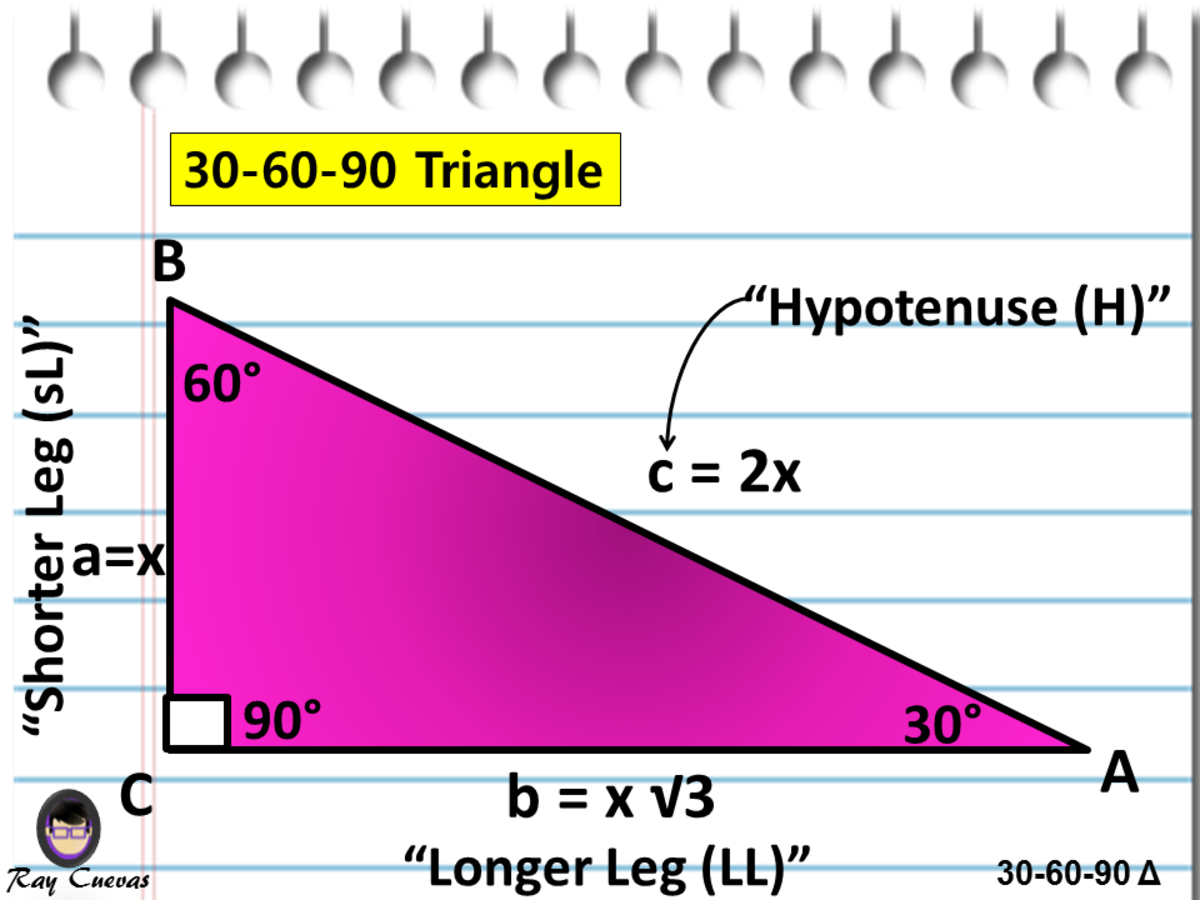
At the core of any 30-60-90 triangle are three angles that total 180 degrees:
- 30 Degrees: The smallest angle, typically adjacent to the shortest side.
- 60 Degrees: The angle opposite the longest side.
- 90 Degrees: The right angle, indicating the triangle's perpendicular nature.
📐 Note: In a 30-60-90 triangle, the hypotenuse (the side opposite the 90-degree angle) is always twice the length of the side opposite the 30-degree angle.
The Magic Ratio
The sides of a 30-60-90 triangle adhere to a special ratio, simplifying calculations:
| Angle | Side Length Ratio |
|---|---|
| 30° | 1 |
| 60° | √3 |
| 90° | 2 |
Forming and Solving 30-60-90 Triangles
To form or solve for any side in a 30-60-90 triangle:
- If you know the shortest side, multiply it by 2 to find the hypotenuse.
- The side opposite the 60-degree angle can be found by multiplying the shortest side by √3.
📐 Note: Always ensure to use the correct proportion when scaling these triangles up or down.
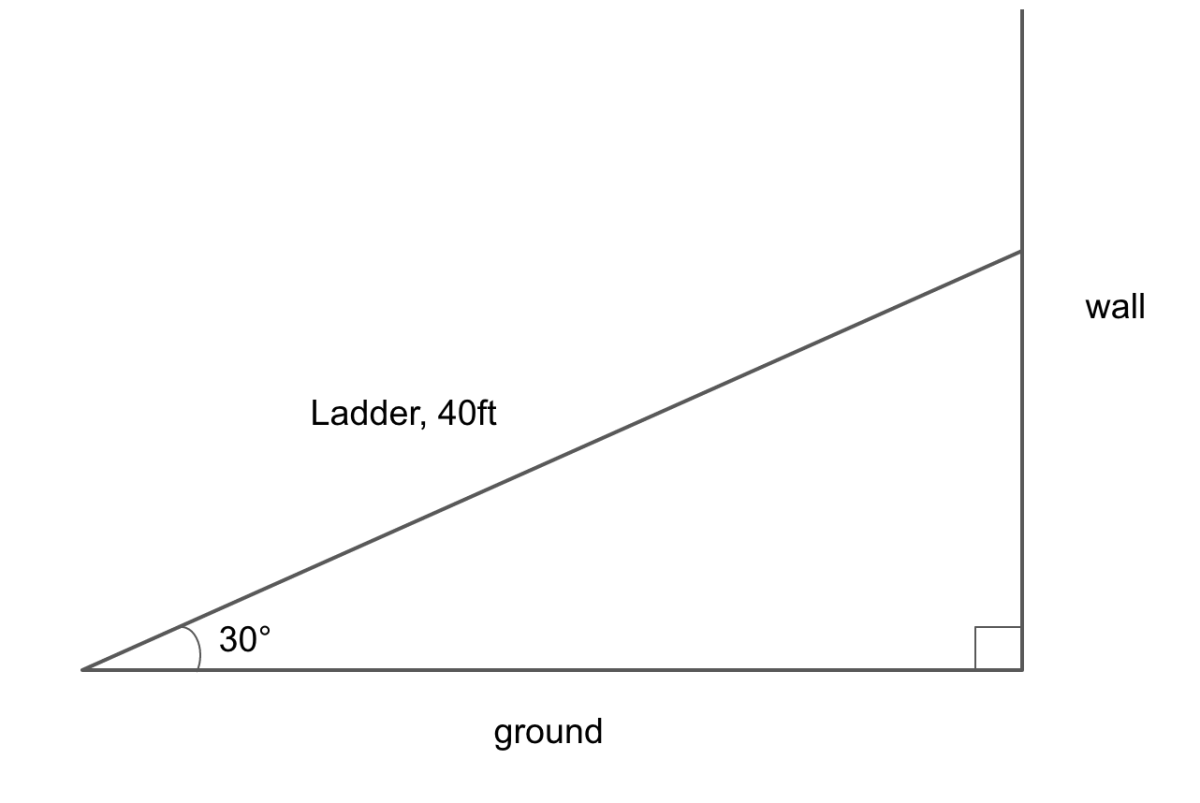
Applications in Real Life
30-60-90 triangles are not just theoretical constructs; they have practical implications in:
- Architectural designs
- Engineering calculations
- Navigation and geometry in video game design
Solving Common Problems
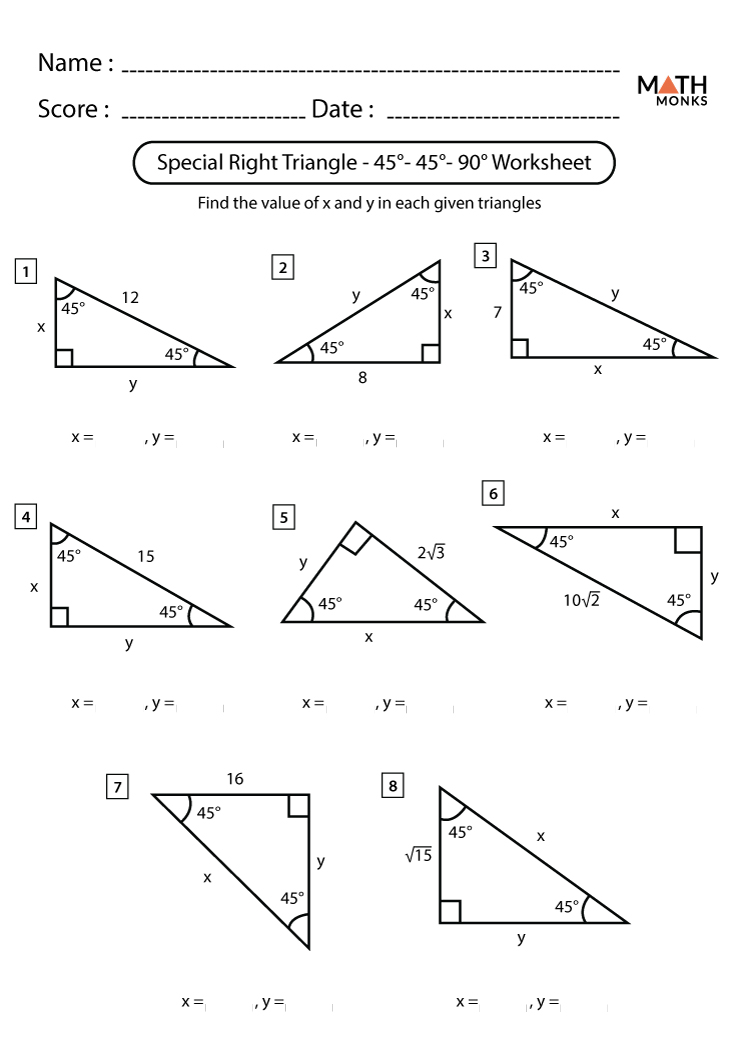
Here are some common scenarios involving 30-60-90 triangles:
- Finding the other sides given one side.
- Using the ratio to calculate angles or sides in more complex shapes.
- Creating models or drawings with precise measurements.
💡 Note: Ensure you understand the significance of the angles and their relationship to the sides for accurate problem-solving.
To summarize, the 30-60-90 triangle is a cornerstone in geometry due to its unique properties, making it invaluable in various fields. Recognizing these triangles can simplify many calculations, from basic trigonometry to advanced architectural design. By understanding and applying the rules governing these triangles, you unlock a world of mathematical and practical applications, enhancing your ability to solve problems with elegance and efficiency.
What are the main characteristics of a 30-60-90 triangle?
+
A 30-60-90 triangle has fixed angles of 30°, 60°, and 90°, with side lengths in the ratio 1:√3:2 for the sides opposite these angles respectively.
Can you use the Pythagorean theorem to verify a 30-60-90 triangle?
+
Yes, the Pythagorean theorem (a² + b² = c²) can be used to verify the relationship between the sides, especially since the hypotenuse is always twice the shortest side.
Why are 30-60-90 triangles important?
+
These triangles are crucial in fields like architecture, engineering, and navigation due to their consistent side ratios and the ease with which angles can be determined from one known side.
