Trigonometry Review Worksheet: Easy Answers and Tips

Trigonometry, a branch of mathematics that studies relationships involving lengths and angles of triangles, often seems daunting to students due to its abstract concepts. However, with the right approach, even complex topics like trigonometric identities, angles, and graphs can be simplified. In this post, we'll review key concepts, provide easy answers to common problems, and share tips to make learning trigonometry more manageable.
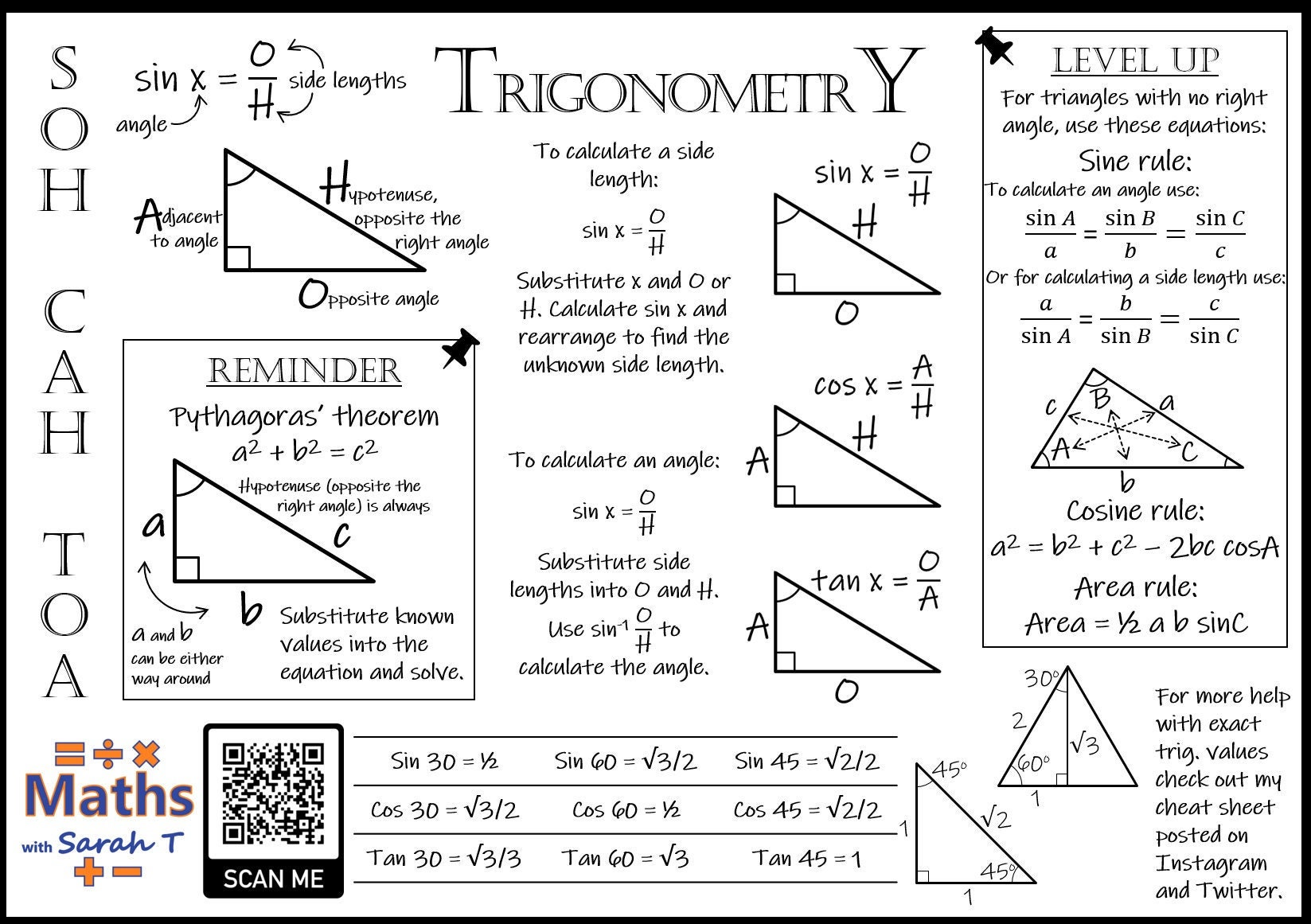
Understanding Trigonometric Ratios


At the heart of trigonometry are the three primary ratios:
- Sine (sin): The ratio of the length of the opposite side to the hypotenuse.
- Cosine (cos): The ratio of the length of the adjacent side to the hypotenuse.
- Tangent (tan): The ratio of the length of the opposite side to the adjacent side.
These ratios are defined in a right-angled triangle and are fundamental for calculating angles or side lengths.
Trigonometric Identities

Understanding trigonometric identities can significantly simplify problem-solving. Here are some of the most useful identities:
- Reciprocal Identities:
sec(θ) = 1/cos(θ),csc(θ) = 1/sin(θ),cot(θ) = 1/tan(θ) - Pythagorean Identities:
sin2(θ) + cos2(θ) = 1 - Sum and Difference Formulas:
sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
💡 Note: Understanding these identities can help in simplifying trigonometric expressions and solving equations.
Tips for Solving Trigonometric Equations

Here are some strategies to approach trigonometric equations:
- Substitution: Sometimes substituting known trigonometric values or identities can simplify complex equations.
- Using Identities: Apply trigonometric identities to transform equations into more manageable forms.
- Graphical Analysis: Use graphs to visualize and solve equations or to estimate solutions graphically.
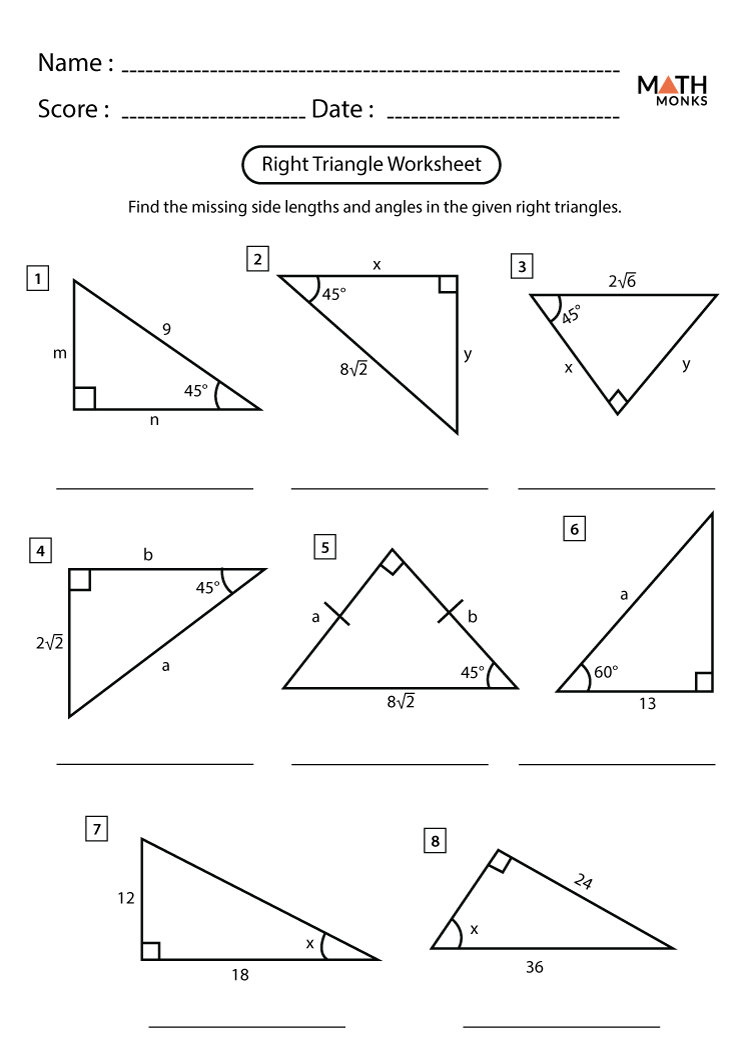
Easy Trigonometry Problems with Answers

Let’s explore some simple problems that can help solidify your understanding:
| Problem | Solution |
|---|---|
| Find sin(θ) if θ = 30° | sin(30°) = 0.5 |
| Calculate tan(θ) if cos(θ) = 0.8 and sin(θ) = 0.6 | tan(θ) = sin(θ)/cos(θ) = 0.6/0.8 = 0.75 |

💡 Note: Always remember the unit circle values for common angles like 0°, 30°, 45°, 60°, 90°.
Trigonometric Graphing Tips

Graphing trigonometric functions can be a powerful tool:
- Amplitude: The amplitude of sine and cosine graphs represents the peak value from the center line.
- Periodicity: The sine, cosine, and tangent functions are periodic; understanding their cycles helps in plotting them.
- Phase Shift: Horizontal shifts of the graph to the left or right affect how the function starts relative to the x-axis.
In summary, trigonometry might initially seem complex due to its abstract nature, but with a clear understanding of basic concepts, identities, and practical application through graphs and tables, it becomes much more accessible. By focusing on the relationships between angles and sides in triangles, and employing the identities and tips provided, students can navigate this mathematical terrain with greater ease.
What are the most common trigonometric errors?

+
Common errors include confusing sine, cosine, and tangent, mixing up radians and degrees, and forgetting to apply trigonometric identities correctly.
How can I memorize trigonometric identities?

+
Using mnemonic devices, practicing regularly, and understanding how identities are derived can help in memorizing them. Also, connecting identities visually through unit circles or graphs can aid memory retention.
What are some practical applications of trigonometry?
+
Trigonometry is used in navigation, surveying, architecture, music, engineering, physics, and even in the analysis of sound waves and vibrations.
Why do I need to learn trigonometry?

+
Trigonometry provides tools for problem-solving in various scientific and engineering fields, enhancing analytical skills and providing a deeper understanding of spatial relationships and periodic phenomena.
How can I improve my skills in trigonometry?
+
Practice regularly, understand the foundational concepts, apply visual aids like graphs, and solve real-world problems to reinforce learning. Also, using technology like graphing calculators or software can provide immediate feedback and visual representations of trigonometric functions.