5 Proven Methods to Solve 3-Variable Equation Problems

5 Proven Methods to Solve 3-Variable Equation Problems
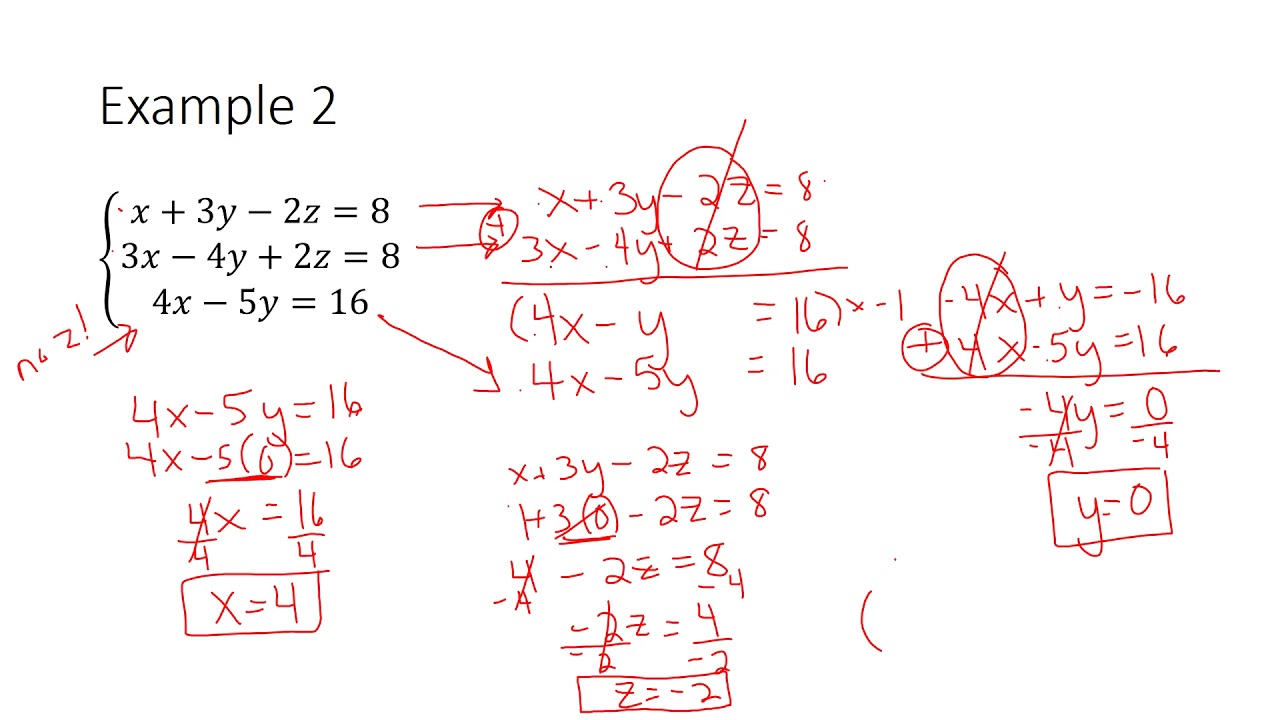
Understanding and solving 3-variable equations can be a daunting task, especially for those new to algebraic concepts. However, with the right approach, these problems can become manageable and even exciting. In this post, we'll explore five proven methods that can help you effectively solve 3-variable equation problems.
1. Substitution Method
The substitution method is one of the most straightforward methods for solving 3-variable equations. Here’s how you can apply it:
- Identify the simplest equation: Look for an equation where you can easily solve for one variable.
- Isolate that variable: Solve for one variable in terms of the others.
- Substitute: Take this expression and plug it into the other equations to eliminate variables progressively.
- Solve for the remaining variables: Continue substituting until you're left with one variable, then solve for it.
📝 Note: Ensure to check your final answer in all original equations for consistency.
2. Elimination Method
The elimination method involves creating a new equation by adding or subtracting equations to eliminate one of the variables. Here’s the step-by-step process:
- Choose equations with coefficients that can easily cancel out: If possible, manipulate the equations so that one of the variables' coefficients matches in sign but not in value.
- Add or subtract the equations: Combine the equations to eliminate one variable.
- Repeat the process: Continue this until you're left with one equation containing one unknown.
- Solve for each variable: After finding one variable, substitute it back to find the others.
This method is particularly useful when the coefficients align in a way that simplifies the process. Here's an example of how it might look:
| Equation 1: | x + y + z = 10 |
| Equation 2: | 2x - y - z = 5 |
| Equation 3: | 3x + y + z = 15 |
| Step: | Add Equation 1 and 2: |
| Result: | 3x = 15, thus x = 5 |

3. Gaussian Elimination

Also known as row reduction, this method systematically eliminates variables by transforming the system of equations into row echelon form:
- Augment the matrix: Create an augmented matrix that includes the constants on the right-hand side.
- Pivot: Use row operations to get a 1 in the top left, then zeros in all cells beneath it.
- Back substitution: After reaching upper triangular form, solve from bottom to top.
⚠️ Note: Gaussian elimination is powerful but can be complex for hand calculations, making it more suitable for computer algorithms.
4. Matrix Method

Solving equations using matrix algebra can be very efficient:
- Formulate the matrix: Write the coefficient matrix and the constant vector.
- Calculate the inverse: Find the inverse of the coefficient matrix.
- Multiply: Solve for the variable vector by multiplying the inverse matrix by the constant vector.
This approach provides a systematic way to solve systems of linear equations when you are comfortable with matrix operations.
5. Cramer’s Rule

Cramer’s Rule uses determinants to solve systems of linear equations:
- Formulate the determinant of the coefficient matrix: Let's call this D.
- Replace columns with constants: Create new determinants for each variable by replacing their respective columns with the constants vector.
- Divide: Each variable is the ratio of these new determinants over D.
Here's an illustrative example:
| System: | 2x + 3y - z = 10 |
| 4x + 2y + 2z = 12 | |
| -3x - 2y + z = 6 | |
| D (Coefficient Determinant): | 2 * (2*1 - 2*(-2)) - 3 * (4*1 - 2*(-3)) + (-1) * (4*(-2) - 2*(-3)) = 17 |
| x = Dx / D: | (10*(2*1 - 2*(-2)) - 3*(12*1 - 6*(-2)) + 6*(12*(-2) - 6*3)) / 17 = 2 |
| y = Dy / D: | ... |
| z = Dz / D: | ... |
These methods provide a broad spectrum of techniques to tackle 3-variable equation problems. Each has its strengths:
- The substitution method is straightforward and intuitive.
- Elimination works well when coefficients naturally align for subtraction or addition.
- Gaussian elimination and matrix method provide structured and systematic solutions ideal for programmable systems.
- Cramer's Rule gives an elegant determinant-based approach.
In summary, solving 3-variable equations involves applying various strategies tailored to the structure of the equations at hand. Whether you prefer the straightforward nature of substitution or the mathematical elegance of matrices, understanding these methods empowers you to conquer even the most complex algebraic challenges. By mastering these techniques, you enhance not only your mathematical prowess but also your ability to model and solve real-world problems that often involve multiple interrelated variables.
What is the benefit of using matrices for solving equations?
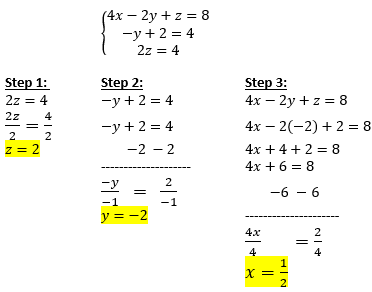
+
Matrices provide a systematic way to handle and solve systems of equations, especially useful for large systems or when using computer programs where manual calculations would be impractical.
When should I use the substitution method instead of elimination?
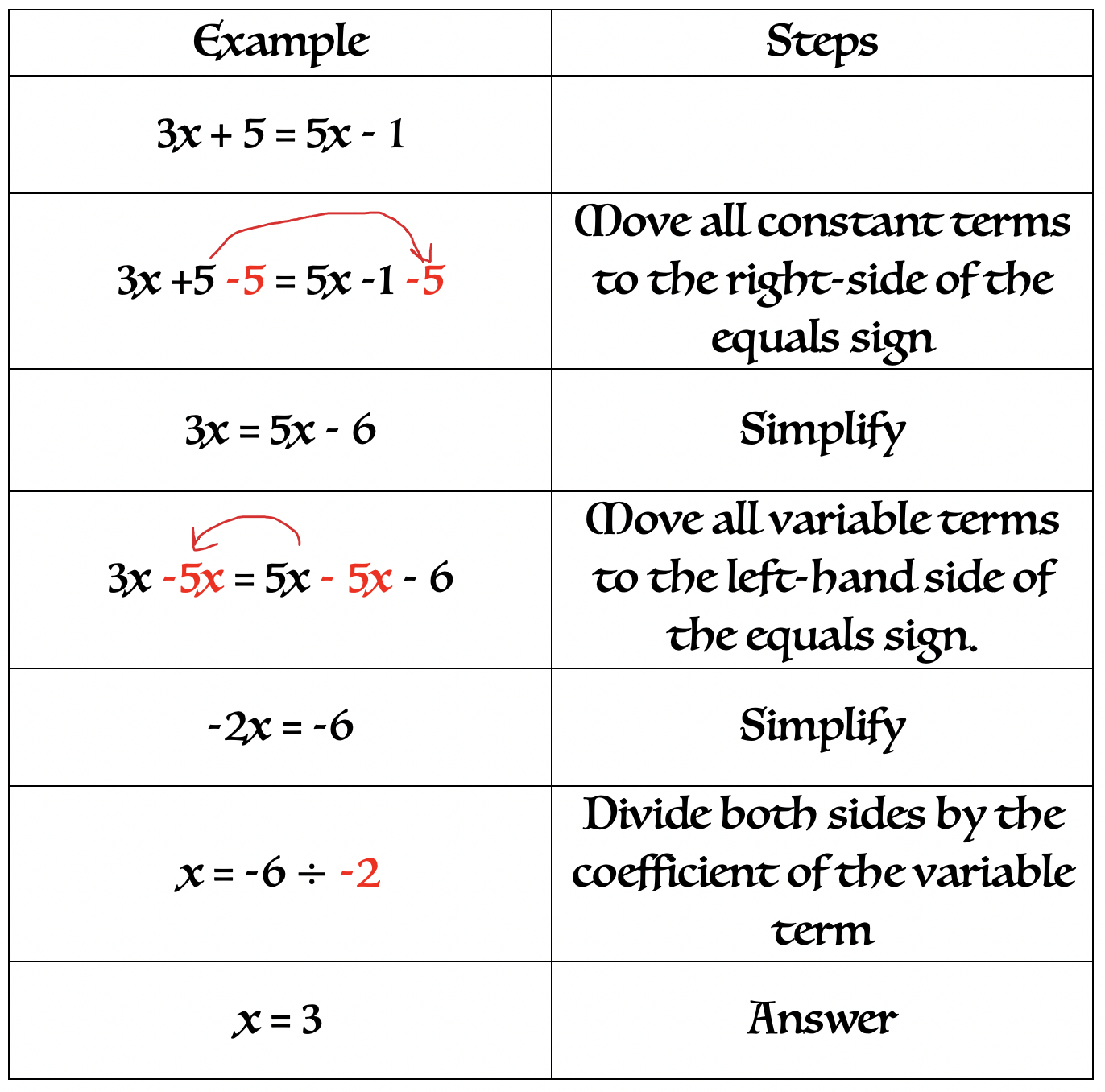
+
Substitution is particularly effective when one variable can be easily isolated from one of the equations, making it simpler to substitute and solve for the other variables.
Can you explain what happens if the determinant in Cramer’s Rule is zero?

+
A zero determinant indicates that the system either has no unique solution or has infinitely many solutions. This can mean the equations are dependent or inconsistent.