5 Proven Methods to Solve Quadratic Equations by Factoring

Mastering Quadratic Equations Through Factoring

Quadratic equations play a crucial role in algebra, often described in the form of ax^2 + bx + c = 0. Solving these equations can unlock numerous applications in both academic and real-world scenarios, such as calculating trajectories in physics or designing electrical circuits. Factoring is one of the most fundamental and insightful methods to solve quadratic equations. Here, we'll explore five proven methods to solve these equations by factoring, making the process both manageable and enjoyable for students and learners.
1. Standard Factoring: The Building Block

Standard factoring, often called “the difference of squares” or “sum and product of roots,” involves finding two binomials whose product equals the original quadratic expression.
- Identify the coefficients (a, b, c) from the standard form (ax^2 + bx + c).
- List down the factors of (a) and (c).
- Combine pairs of factors to find the product that matches (b) when added or subtracted.
- Express the quadratic in factored form ((rx + s)(tx + u)), where (r \cdot t = a) and (s \cdot u = c).
🔎 Note: Factoring works best when the leading coefficient a equals 1 or has simple factors.
2. The Grouping Method

This technique is particularly useful when the quadratic expression isn’t easily factorable by the standard method:
- Rearrange the terms into groups that can be factored separately.
- Factor out the GCF (greatest common factor) from each group.
- If successful, you’ll see a common factor across the entire expression, which can then be factored out.
💡 Note: The grouping method might require you to experiment with term arrangements to find a factorable grouping.
3. Sum and Difference of Cubes

Although not as commonly used for quadratic equations, understanding these patterns can be beneficial when factoring:
- Sum of cubes: (a^3 + b^3 = (a + b)(a^2 - ab + b^2))
- Difference of cubes: (a^3 - b^3 = (a - b)(a^2 + ab + b^2))
- Look for these forms in quadratics by factoring out constants or changing the variable to simplify the problem.
| Expression | Factored Form |
|---|---|
| 8x^3 + 27 | (2x + 3)(4x^2 - 6x + 9) |
| 125x^3 - 216 | (5x - 6)(25x^2 + 30x + 36) |

4. Completing the Square

Not purely a factoring method, completing the square sets the stage for solving quadratics and sometimes provides insight into why factoring might work:
- Transform the quadratic into a perfect square trinomial.
- The process involves manipulating (ax^2 + bx + c) to become (a(x - h)^2 + k), where (h) and (k) are constants.
- Once in square form, factoring can be applied to solve for (x).
📚 Note: Completing the square helps reveal the vertex of a parabola and has applications beyond solving equations.
5. Synthetic Division
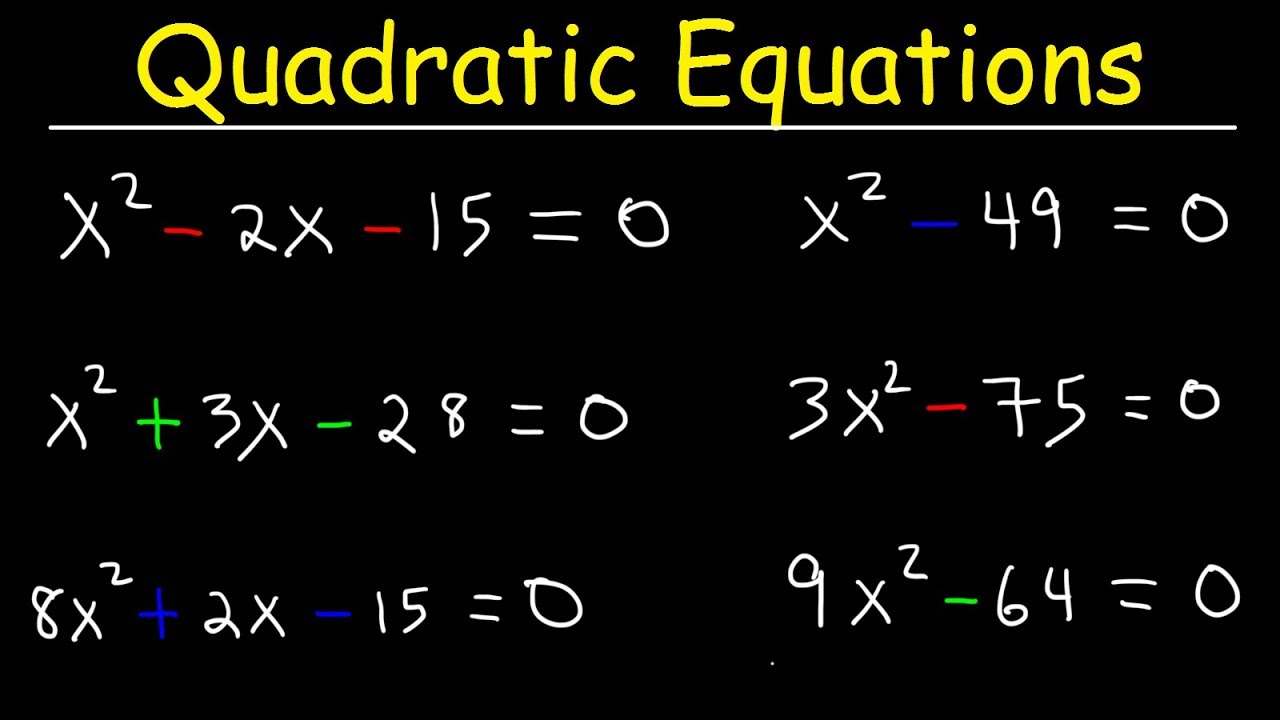
For polynomials of higher degrees, synthetic division can simplify the process of finding roots and factoring. Here’s how to apply it to quadratics:
- Guess a root using the Rational Root Theorem or another method.
- Set up synthetic division with the root as the divisor.
- If division is successful (remainder = 0), the resulting polynomial can often be factored easily.
🔬 Note: Synthetic division streamlines factoring when one or more roots are known or easily guessed.
In sum, by mastering these methods, you’ll gain powerful tools for solving not just quadratic equations but also polynomials of higher degrees. Each method provides unique insights into the nature of polynomials, enhancing your mathematical understanding and problem-solving skills. These techniques showcase the beauty of factoring, transforming complex problems into simple, elegant solutions.
Why is factoring important in solving quadratic equations?

+
Factoring allows you to find the roots of the equation more efficiently and understand the equation’s structure, which is crucial for both solving and interpreting mathematical models.
Can all quadratic equations be solved by factoring?

+
No, not all quadratic equations are factorable over the real numbers, but factoring is often the first step tried due to its simplicity and effectiveness when applicable.
What if I can’t factor a quadratic equation?

+
Use alternative methods like the quadratic formula, completing the square, or graphical methods to solve quadratic equations that are not factorable.
Is there any advantage to using synthetic division over other methods?

+
Yes, synthetic division can be faster when you have a root or when working with higher-degree polynomials. It’s particularly useful for polynomial division.
How does factoring help in real-world applications?

+
Factoring is used in physics, engineering, and economics to model behaviors, optimize functions, and solve equations that describe real-world scenarios.