Trigonometry Basics: Label Triangles Like a Pro

Have you ever struggled with solving mathematical problems involving angles and triangles? The ancient Greeks knew it, the Renaissance polymaths mastered it, and today, it's a cornerstone of mathematics and physics: Trigonometry. Whether you're calculating the height of a building, navigating the stars, or analyzing electrical circuits, understanding trigonometry is crucial. In this long-form blog post, we'll dive deep into the basics of trigonometry, with a specific focus on one of the most fundamental tasks: labeling triangles like a pro. This skill not only aids in problem-solving but also enhances your understanding of how trigonometry applies to real-world scenarios.
Understanding Triangles
Triangles are the simplest polygons, with three sides, three vertices, and three angles that always add up to 180 degrees. They can be classified by their sides (equilateral, isosceles, scalene) or angles (acute, right, obtuse, equiangular).
Types of Triangles

- Equilateral: All sides and angles are equal (60 degrees).
- Isosceles: Two sides are equal, and the angles opposite these sides are equal.
- Scalene: All sides and angles are different.
- Right: Contains one 90-degree angle.
- Acute: All angles are less than 90 degrees.
- Obtuse: One angle is more than 90 degrees.
📐 Note: The sum of internal angles in any triangle is always 180 degrees.
The Essence of Trigonometry

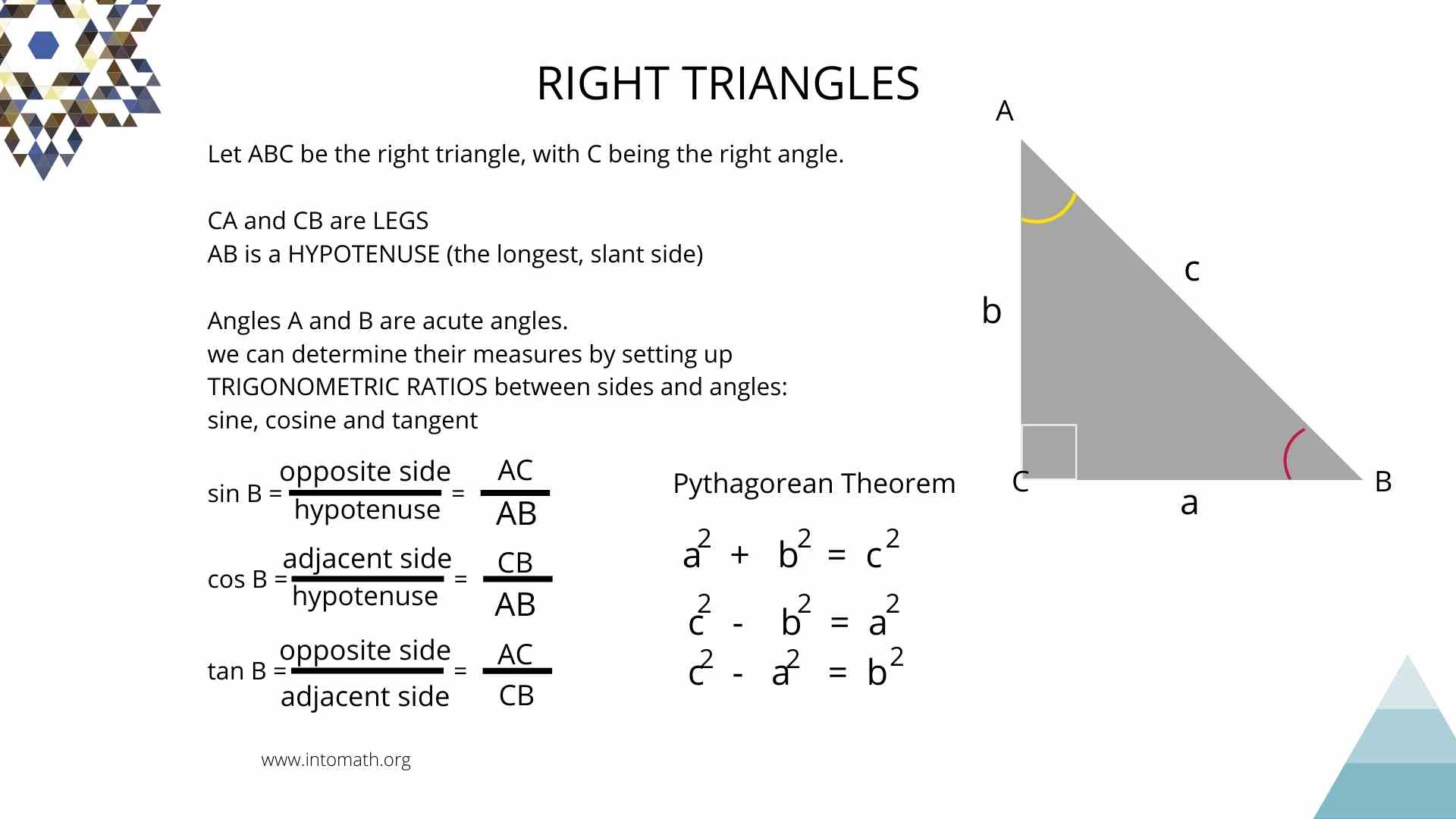
Trigonometry, derived from Greek words meaning "triangle measurement," deals with the relationships between the sides and angles of triangles. The primary focus is on right triangles where one of the angles is 90 degrees, but the principles can extend to other types as well.
The Trigonometric Ratios

The most common trigonometric ratios are:
- Sine (sin): Opposite/Hypotenuse
- Cosine (cos): Adjacent/Hypotenuse
- Tangent (tan): Opposite/Adjacent
- Cotangent (cot): Adjacent/Opposite
- Secant (sec): Hypotenuse/Adjacent
- Cosecant (csc): Hypotenuse/Opposite
These ratios can be used to calculate unknown sides or angles when given the other two components of the triangle.
Labeling Triangles for Trigonometry

When you are dealing with trigonometry, correctly labeling a triangle is the first step towards solving problems efficiently. Here's how you can label triangles effectively:
Identify the Sides

In a right triangle:
- The Hypotenuse is the longest side, opposite the right angle.
- The Opposite side is opposite to the angle you're focusing on.
- The Adjacent side is next to the angle in question.
| Label | Description |
|---|---|
| Hypotenuse | Longest side, opposite the right angle |
| Opposite | Side opposite to the angle you're working with |
| Adjacent | Side next to the angle you're working with |

Labeling with Respect to Angles

Here’s how you might label a right triangle:
- If angle θ is labeled, the side opposite to θ is the Opposite side.
- The side next to θ is labeled as Adjacent.
- The hypotenuse remains the hypotenuse regardless of the angle in focus.
🔄 Note: Remember that these labels will change if you switch your focus to a different angle within the same triangle.
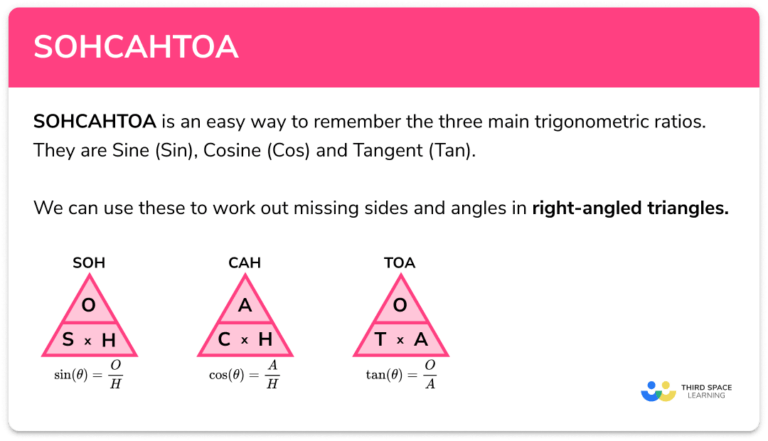
Using SOH-CAH-TOA
SOH-CAH-TOA is a mnemonic to remember the relationships between angles and sides in right triangles:
- Sine (SOH): Sin(θ) = Opposite / Hypotenuse
- Cosine (CAH): Cos(θ) = Adjacent / Hypotenuse
- Tangent (TOA): Tan(θ) = Opposite / Adjacent
By understanding these ratios, you can determine any side or angle when provided with the other necessary information.
Practical Applications

Labeling triangles is not just a theoretical exercise; it has practical applications in:
- Construction: Calculating angles for roofs or beams.
- Physics: Analyzing forces in vector components.
- Navigation: Determining bearings and distances.
- Surveying: Calculating heights and distances of inaccessible points.
By correctly labeling the triangles involved in these applications, you can derive the necessary measurements with precision.
Common Mistakes and How to Avoid Them

Here are some common pitfalls to avoid when labeling and solving trigonometric problems:
- Misidentifying Angles: Always check which angle you're focusing on to label sides correctly.
- Incorrect Use of Trigonometric Ratios: Misapplying sine, cosine, or tangent can lead to wrong calculations.
- Ignoring Angle Sizes: Remember that a triangle's angles must sum to 180 degrees.
🚨 Note: Double-check your labeling before you start solving, especially in complex problems involving multiple triangles.
Conclusion: Mastering Triangle Labeling

Labeling triangles in trigonometry is foundational yet essential. By understanding and correctly applying the rules, you enable yourself to solve a wide range of problems from the simplest right triangles to complex geometric puzzles. Remember, every correctly labeled triangle is a step towards deeper understanding, better problem-solving, and precise applications in real-world scenarios.
What are the primary trigonometric ratios?
+
The primary trigonometric ratios are sine, cosine, and tangent, abbreviated as sin(θ), cos(θ), and tan(θ) respectively. These ratios relate the angles of a right triangle to the lengths of its sides.
Can trigonometric principles be applied to triangles other than right triangles?

+
Yes, while the basic trigonometric ratios are defined for right triangles, they can be extended through the law of sines and law of cosines to solve any type of triangle, whether it’s acute, right, or obtuse.
Why is correct labeling important in trigonometry?

+
Correct labeling is crucial because it ensures you are using the right trigonometric functions in calculations. Mislabeling can lead to using the wrong ratio, resulting in incorrect problem solving.