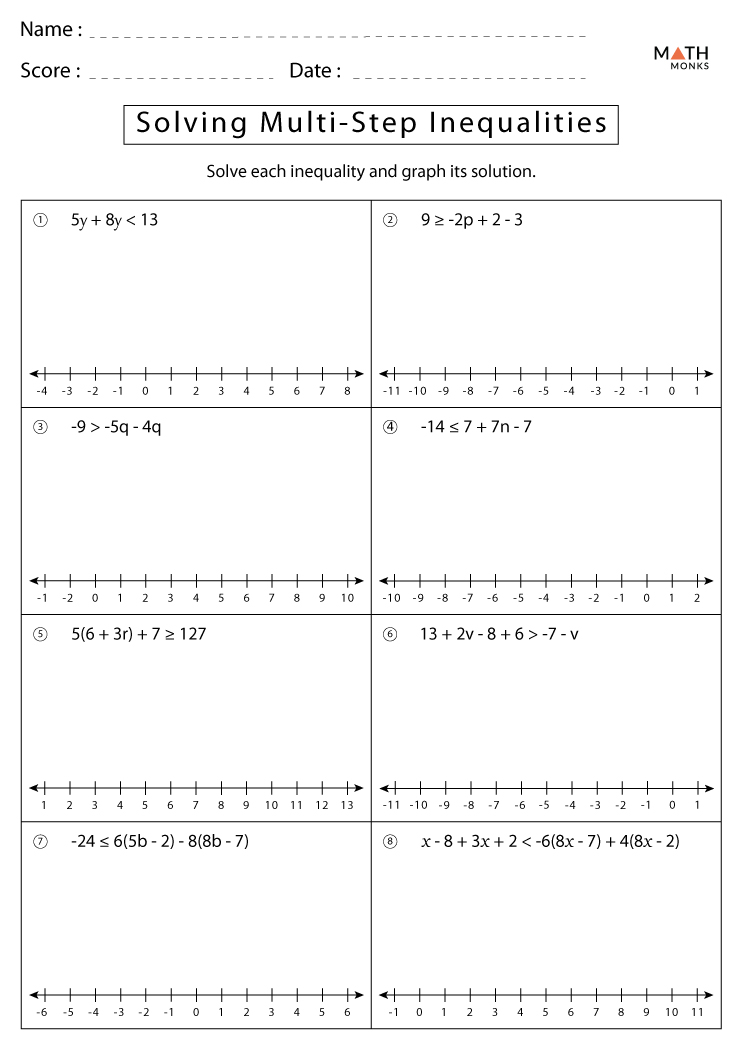
5 Easy Steps for Solving Multi-Step Inequalities

Solving multi-step inequalities can initially seem daunting. However, breaking them down into manageable steps can simplify the process significantly. This blog post will guide you through 5 easy steps to conquer multi-step inequalities, ensuring that you can solve them with confidence and ease.
Understanding Inequalities

Before diving into the steps, it’s crucial to understand what inequalities are. Unlike equations where the two expressions are equal, inequalities express a relationship where one side is less than, less than or equal to, greater than, or greater than or equal to the other. The symbols used are: < (less than), ≤ (less than or equal to), > (greater than), and ≥ (greater than or equal to).
Step 1: Eliminate Parentheses

If your inequality contains parentheses, your first step is to distribute any constants outside the parentheses to every term within:
- Example: Solve 3(x + 2) ≤ 15
- Distribute: 3x + 6 ≤ 15
⚠️ Note: Remember that when distributing a negative, every term inside the parentheses changes sign.
Step 2: Combine Like Terms
Next, simplify both sides of the inequality by combining like terms:
- Example: Solve 4x - 2 + 3x < 6
- Combine: 7x - 2 < 6
⚠️ Note: This step might not always be necessary if there are no like terms to combine.
Step 3: Isolate the Variable

Here, you will start moving terms that contain the variable (x in most cases) to one side of the inequality. Remember:
- If you add or subtract a number from one side, do the same to the other side.
- If you multiply or divide both sides by a positive number, the inequality remains the same.
- Example: 7x - 2 < 6
- Add 2: 7x < 8
- Divide by 7: x < 8⁄7
⚠️ Note: If multiplying or dividing by a negative number, reverse the inequality sign.
Step 4: Check for Invalid Operations

Ensure you haven’t performed any operations that would invalidate the inequality, such as:
- Multiplying or dividing by zero
- Taking the square root of a negative number
- Dividing by variables that might be zero
This step involves looking at your work critically to avoid common mistakes.
Step 5: Represent the Solution on a Number Line or in Interval Notation

Once you’ve isolated your variable, your solution can be represented either:
- Number Line: Draw a number line and shade the appropriate section. Use open circles for strict inequalities ( <, > ) and closed circles for non-strict inequalities ( ≤, ≥ ).
- Interval Notation: Write the solution using parentheses ( ) for strict inequalities or brackets [ ] for non-strict inequalities.
| Inequality | Number Line Representation | Interval Notation |
|---|---|---|
| x < 4 |  |
(-∞, 4) |
| x ≥ -2 |  |
[-2, ∞) |

After following these five steps, you should now have a clear solution to your multi-step inequality. Solving these types of problems becomes more intuitive with practice, allowing you to tackle even more complex algebraic inequalities in the future.
What do I do if my inequality involves division by a variable?

+
Be cautious when dividing by a variable because if that variable equals zero, the operation would be invalid. In such cases, you must consider both conditions: one where the variable is not zero and proceed with your solution, and another where the variable equals zero, which might give you an additional condition or solution to consider.
How can I check my solution to a multi-step inequality?

+
To check your solution, choose any number within the solution set and substitute it back into the original inequality. If the inequality holds true, your solution is correct.
Can I always use the same steps to solve any multi-step inequality?
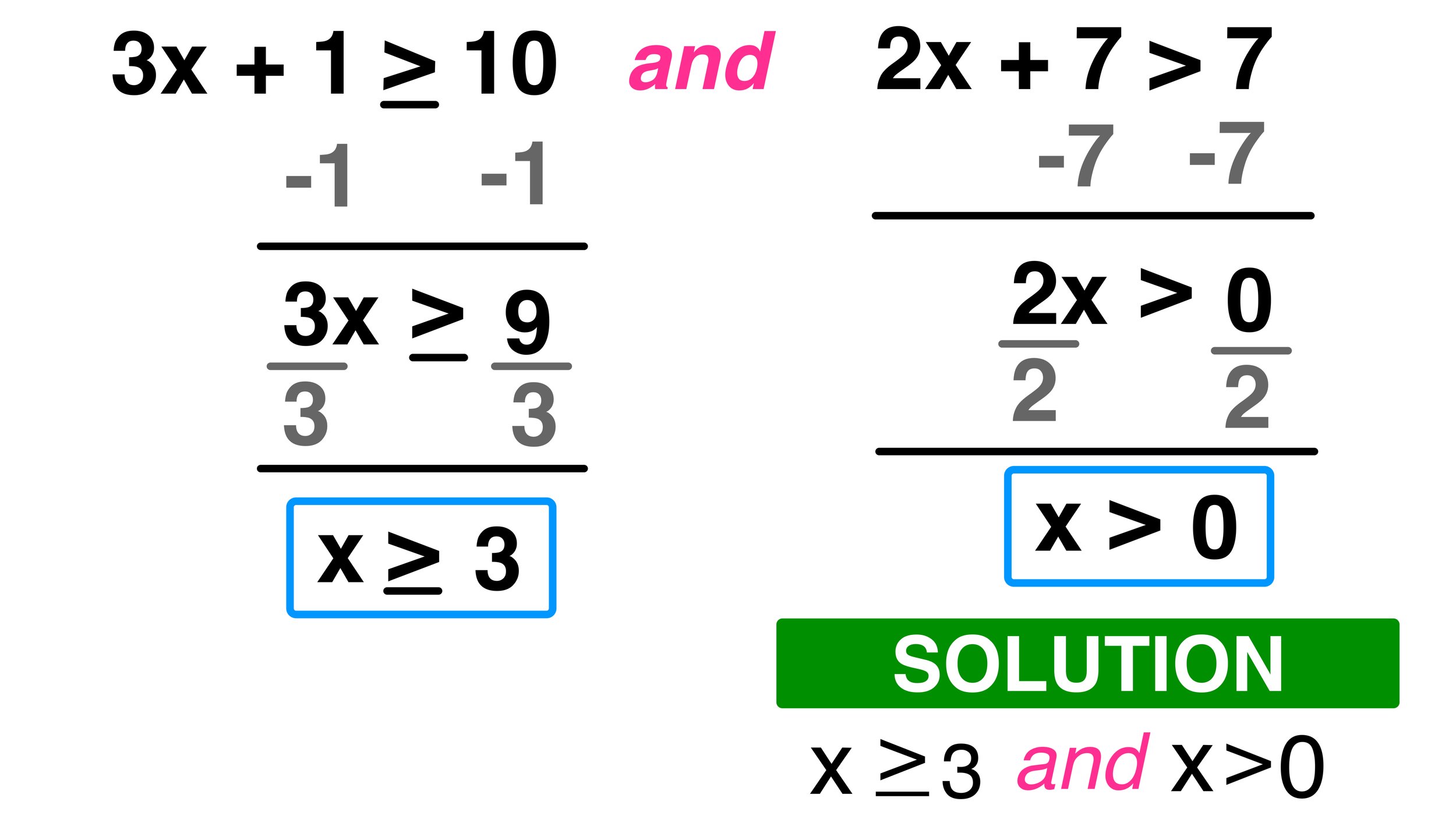
+
Yes, these steps are a general guide. However, some inequalities might require special considerations like dealing with absolute values or quadratic expressions, where additional techniques might be needed.