5 Easy Steps to Master Equivalent Fractions

Understanding equivalent fractions is essential for both basic arithmetic and advanced mathematics, providing a foundational skill set that enhances overall numerical literacy. Whether you're helping a child with their homework, brushing up on your own skills, or looking to improve your understanding of mathematics for various applications, mastering equivalent fractions can unlock numerous mathematical doors.
Step 1: Understand the Concept of Equivalent Fractions

Equivalent fractions are fractions that represent the same value, even though they might appear different at first glance. Here’s how to grasp the concept:
- Visualization: Imagine a whole pie. If you divide it into two equal parts, each part represents 1⁄2. If you divide that same pie into four parts, each part is now 1⁄4, but two parts together still represent the whole pie or 2⁄4. Both 1⁄2 and 2⁄4 are equivalent.
- Multiplication and Division: Equivalent fractions are created by multiplying or dividing both the numerator (top number) and the denominator (bottom number) by the same non-zero number.
✍️ Note: Multiplying or dividing by 1 has no effect on the fraction, so choose any number but 1 to find an equivalent fraction.
Step 2: Creating Equivalent Fractions
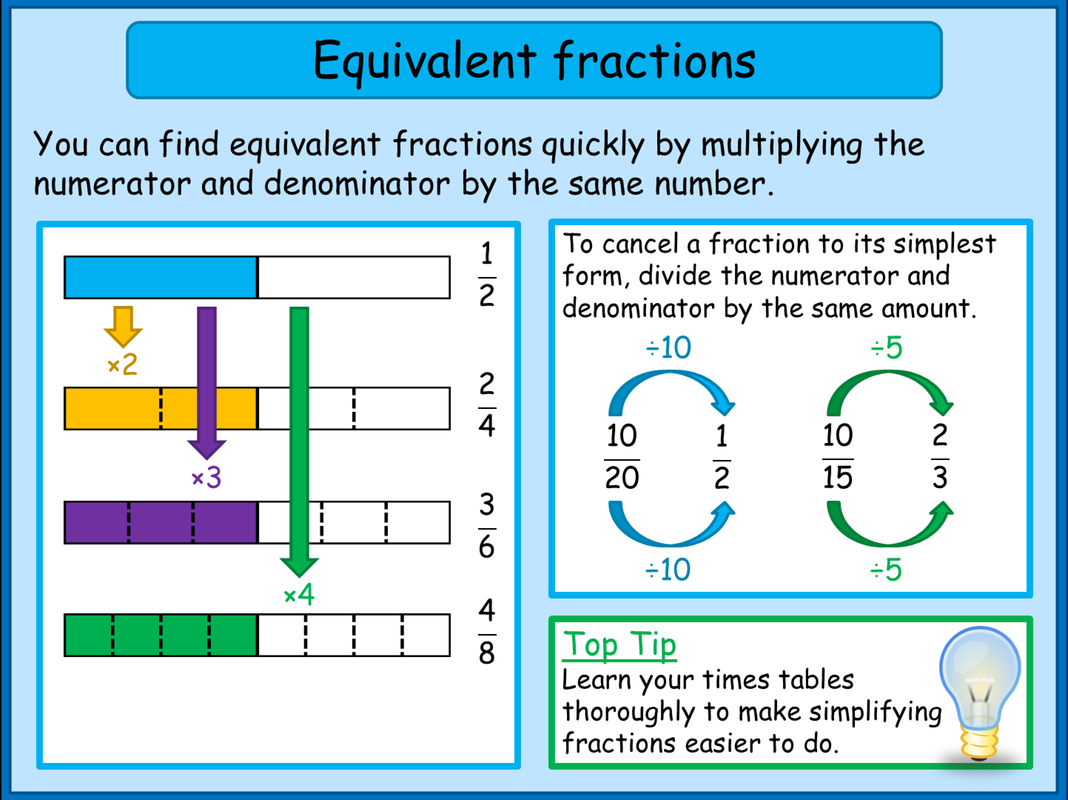
The process of creating equivalent fractions involves simple multiplication or division:
- Multiplication: If you have the fraction 3⁄4, to find an equivalent fraction, multiply both numbers by the same value. For example, multiply by 2 to get 6⁄8.
- Division: Similarly, if you need to simplify a fraction, divide both numbers by the same value. For instance, 6⁄8 can be simplified by dividing both numbers by 2, yielding 3⁄4.
Here is a table to illustrate:
| Fraction | Multiplication/Division by | Equivalent Fraction |
|---|---|---|
| 3⁄4 | ×2 | 6⁄8 |
| 6⁄8 | ÷2 | 3⁄4 |
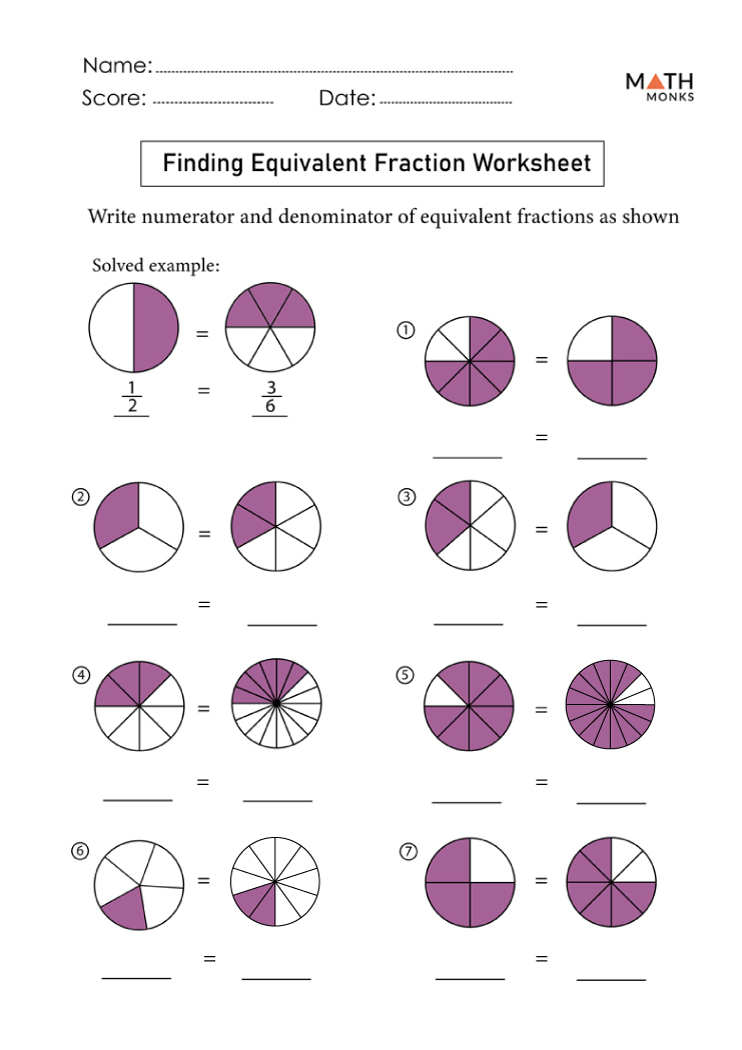
Step 3: Simplifying Fractions

The goal of simplifying fractions is to express them in their lowest terms, which means you can’t simplify them further:
- Greatest Common Divisor (GCD): Find the largest number that divides both the numerator and the denominator without leaving a remainder.
- Method: Divide both the numerator and the denominator by their GCD until no further simplification is possible.
Step 4: Finding a Common Denominator

When working with multiple fractions, a common operation is to find a common denominator to compare or add them:
- Least Common Multiple (LCM): Determine the smallest number that all denominators can divide evenly into. This number becomes the common denominator.
- Adjust Fractions: Adjust each fraction so that they all have the same denominator, making it easier to perform operations.
⚠️ Note: This step is crucial when adding or subtracting fractions because fractions must share a common denominator for these operations to be valid.
Step 5: Practice and Real-World Application
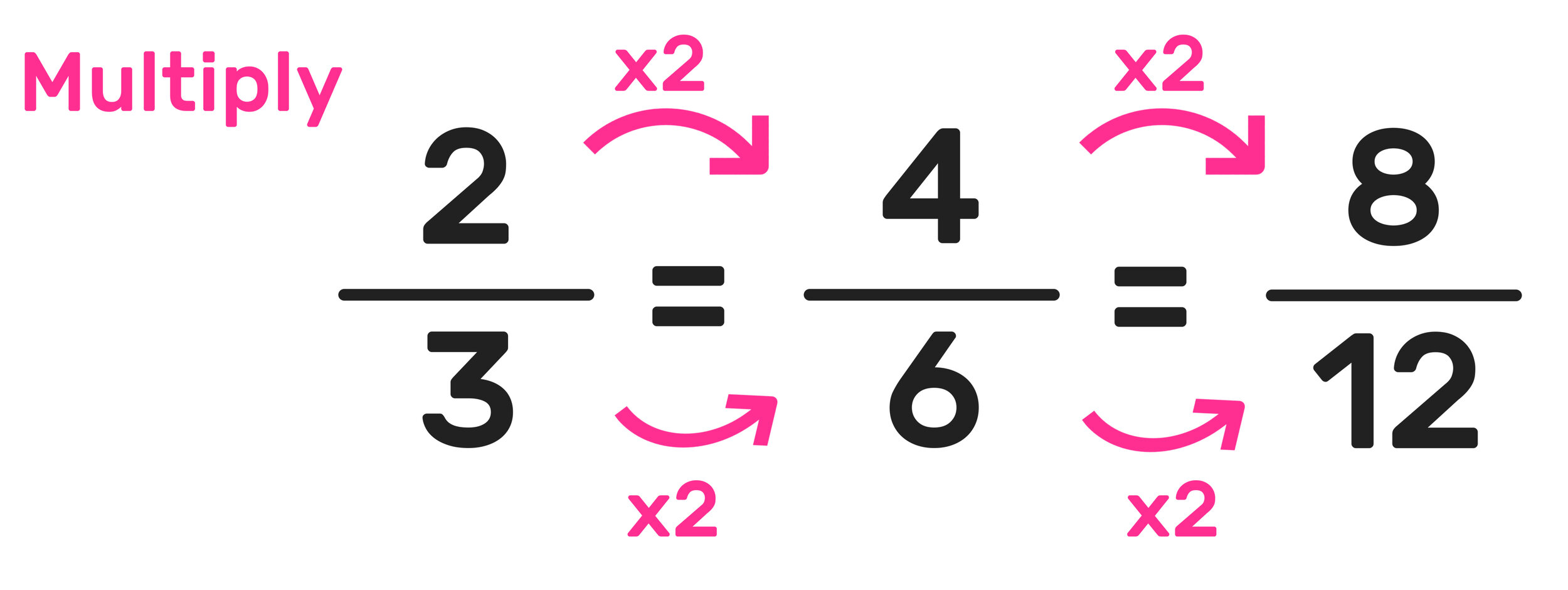
The final step to mastering equivalent fractions is consistent practice:
- Repetition: Engage in exercises that involve finding equivalent fractions, simplifying, and working with common denominators.
- Applications: Use real-world scenarios, like dividing a pizza or sharing resources, to make the concept more tangible.
Understanding and working with equivalent fractions can dramatically improve your comfort with arithmetic and pave the way for more complex mathematical concepts. This skill is not just academic; it has practical uses in everyday life, from cooking to financial planning.
In wrapping up, the journey to mastering equivalent fractions involves understanding the concept, learning to create and simplify fractions, finding common denominators, and practicing regularly. Each step builds upon the previous one, creating a comprehensive understanding that can be applied in numerous contexts. Whether for solving equations, improving your child's math skills, or tackling everyday calculations, the knowledge of equivalent fractions is invaluable. The key takeaway is that fractions, like numbers, are a language of patterns and relationships, revealing the interconnectedness of mathematics.
Why are equivalent fractions important?

+
Equivalent fractions are crucial because they allow us to compare, add, or subtract fractions more easily. They also help in understanding the relationship between different fractional values, making complex mathematical operations simpler.
What’s the difference between simplifying and finding a common denominator?

+
Simplifying a fraction means reducing it to its smallest form where no further division is possible. Finding a common denominator, on the other hand, is about making multiple fractions have the same denominator so they can be operated on together.
How can I make equivalent fractions more intuitive?

+
Think of fractions in terms of real-world examples like sharing a pizza or dividing a cake. Visualizing fractions this way can make their equivalence more apparent. Also, regular practice with exercises and puzzles can sharpen your understanding.