2 Step Inequalities Worksheet: Mastering Math Skills Easily
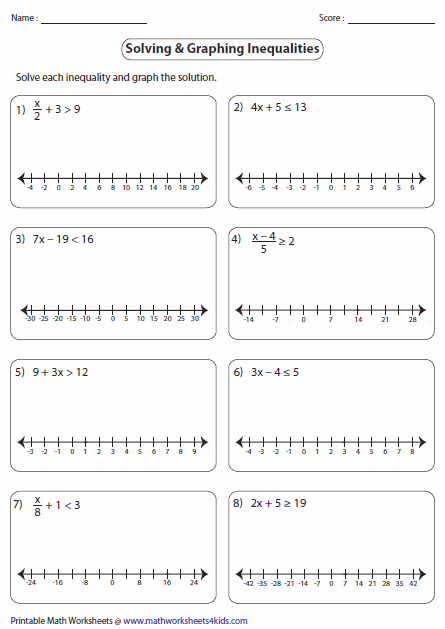
Are you struggling with two-step inequalities and wish to gain proficiency in solving them? Understanding how to handle these inequalities is a crucial math skill that often lays the groundwork for more advanced algebra and calculus. In this comprehensive guide, we will walk you through a series of steps and examples to make mastering two-step inequalities as straightforward as possible. Let's dive in!
What are Two-Step Inequalities?

Two-step inequalities, as the name suggests, require two operations to isolate the variable. They look much like equations, but instead of an equal sign (=), you’ll find inequality signs such as <, >, ≤, or ≥.
Here's a basic example:
| 3x + 4 > 7 |

💡 Note: When solving inequalities, remember that the direction of the inequality sign changes if you multiply or divide both sides by a negative number.
Steps to Solve Two-Step Inequalities

Let’s break down the process into easy-to-follow steps:
Step 1: Isolate the Term with the Variable

Start by moving any constant term on the same side as the variable to the other side of the inequality using addition or subtraction. For instance:
- Given: 3x + 4 > 7
- Subtract 4 from both sides: 3x + 4 - 4 > 7 - 4
- Simplify: 3x > 3
Step 2: Solve for the Variable

Now, isolate the variable by performing the inverse operation of multiplication or division:
- Given: 3x > 3
- Divide both sides by 3: (3x)/3 > 3⁄3
- Simplify: x > 1
Remember, if you are dividing or multiplying by a negative number, you must reverse the inequality sign:
- Given: -2x - 5 ≤ 1
- Add 5 to both sides: -2x ≤ 6
- Divide both sides by -2 and reverse the sign: x ≥ -3
🚨 Note: Always check your work by substituting values from the solution set back into the original inequality to ensure they satisfy the inequality.
Common Mistakes to Avoid
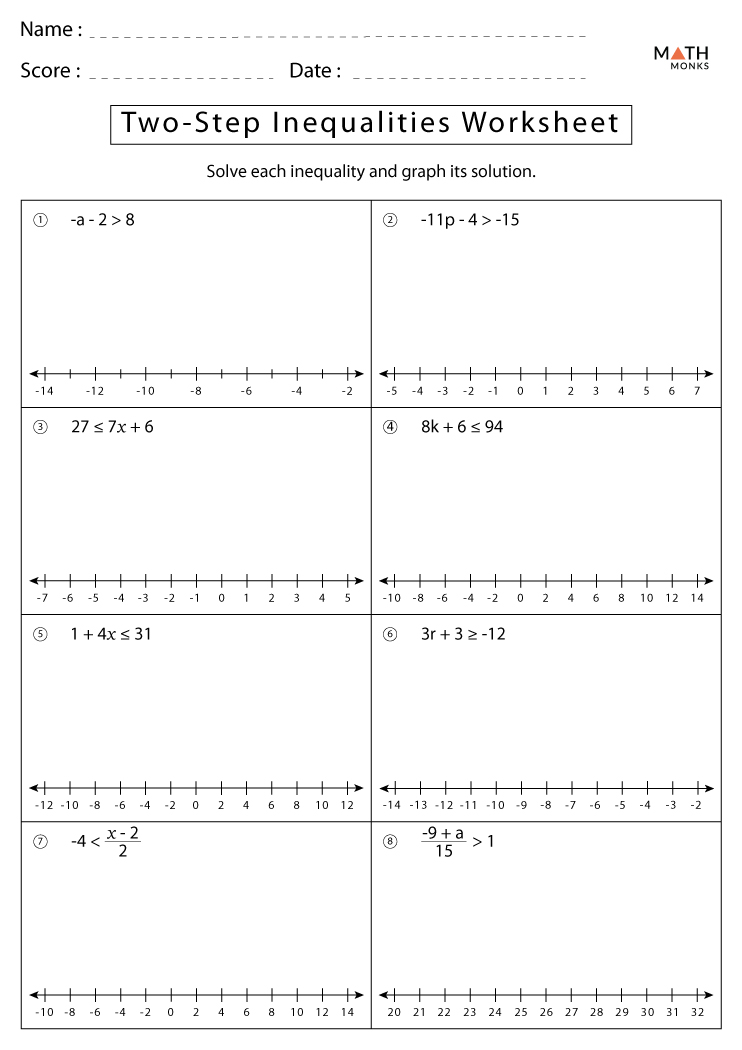
Here are some common errors students make when solving two-step inequalities:
- Not flipping the inequality sign: When multiplying or dividing by a negative number, it’s critical to flip the inequality sign.
- Misinterpreting the inequality: Be cautious with the direction of the inequality sign throughout your solving process.
- Forget to isolate variable term first: Always ensure to get rid of constants before solving for the variable.
Worksheet for Practice

Let’s solidify your understanding with a set of exercises. Here’s a worksheet you can use for practice:
- Solve for x in each inequality:
- 2x + 3 < 11
- 3x - 5 ≥ 10
- -x + 4 > 8
- 5 - 2x ≤ -3
- 4x + 6 ≤ 18
These problems will give you a practical application of the steps we've discussed, allowing you to gain confidence in solving two-step inequalities.
📝 Note: Use pencil and paper or a whiteboard to work through these problems. Visualizing the steps can significantly help in understanding and retaining the process.
Summing Up

We’ve journeyed through the basics of two-step inequalities, outlined the step-by-step process to solve them, and highlighted common pitfalls. Remember, the key to mastering these inequalities lies in consistent practice and understanding the underlying principles. By following the structured approach we’ve provided, you’re well on your way to becoming proficient in solving inequalities with ease.
Why do we need to flip the inequality sign?

+
Flipping the inequality sign when multiplying or dividing by a negative number ensures that the relationship between the terms remains consistent. This operation effectively ‘swaps’ the values on both sides, necessitating a change in direction to preserve the original inequality’s truth.
Can inequalities have multiple solutions?

+
Yes, inequalities typically have a range of solutions rather than a single solution, especially in real-world applications where ‘less than’ or ‘greater than’ scenarios are common.
How do you know if an inequality is solved correctly?

+
To verify the solution, substitute a value from the solution set back into the original inequality. If it holds true, your solution is likely correct. Also, checking boundary values (the points where the inequality changes from true to false) can be useful.