5 Essential Tips for Mastering Growth and Decay Formulas

Growth and decay are fundamental concepts in various scientific fields, ranging from physics to biology and finance. Understanding these formulas helps predict how quantities change over time, either increasing (growth) or decreasing (decay). Whether you're studying exponential growth in investments, population dynamics, or radioactive decay, mastering these formulas can significantly enhance your analytical skills. Here are five essential tips to master growth and decay formulas effectively:
1. Grasp the Basics
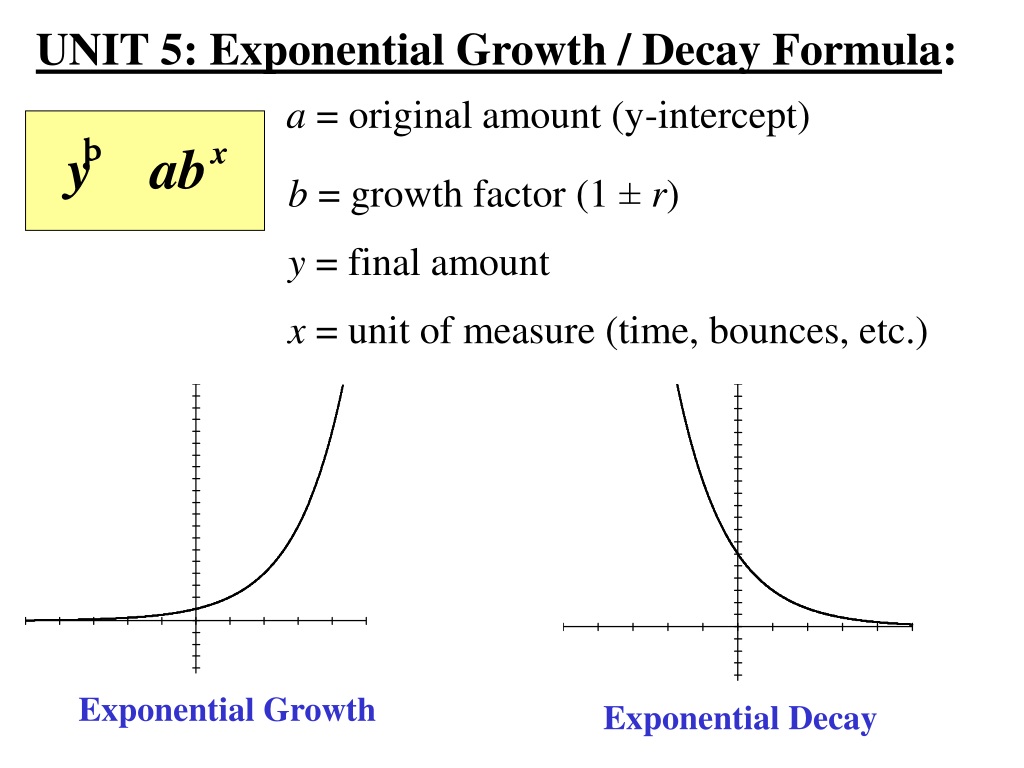
Before diving into complex problems, make sure you have a firm grip on the basic formula for exponential growth and decay:
- Exponential Growth: ( P(t) = P_0 e^{rt} )
- Exponential Decay: ( P(t) = P_0 e^{-rt} )
Where:
- P(t) is the quantity after time (t)
- P_0 is the initial quantity
- r is the growth or decay rate
- e is Euler’s number (approximately 2.71828)
🔍 Note: Euler’s number (e) is crucial for understanding continuous growth and decay processes.
2. Apply Real-World Context

Linking mathematical concepts to real-life scenarios can solidify your understanding:
- Population Growth: Use the formula to predict population changes in different species or human cities.
- Finance: Calculate how investments grow over time or how debt decays with interest.
- Medicine: Determine the decay rate of medications or isotopes in the body for dosage calculations.
By using actual data or hypothetical scenarios, you can see how these formulas behave under different conditions.
3. Practice with Variations

Exponential growth and decay come with variations:
- Logistic Growth: For populations with resource limits.
- Half-Life: Common in nuclear physics for radioactive decay.
| Model | Formula |
|---|---|
| Logistic Growth | [ P(t) = \frac{K}{1 + \left(\frac{K - P_0}{P_0}\right) e^{-rt}} ] |
| Half-Life | [ N(t) = N0 \cdot \left(\frac{1}{2}\right)^{\frac{t}{t{1⁄2}}} ] |

📝 Note: Understanding these variations will broaden your problem-solving capabilities in various contexts.
4. Use Technology Effectively

Technology can significantly aid in mastering these concepts:
- Calculators: Use scientific or graphing calculators to calculate complex expressions and visualize growth curves.
- Spreadsheet Software: Create models to see how values change over time by plotting data.
- Software Tools: Programs like MATLAB or Python with libraries like NumPy can simulate complex growth and decay scenarios.
5. Reflect and Review

After working through problems, take time to reflect:
- Review the Formulas: Go back to the basics to ensure your understanding.
- Ask Critical Questions: How do small changes in the growth rate affect the outcome? What happens if you double the decay rate?
- Summarize: Write summaries of what you’ve learned or share explanations with peers.
Mastering growth and decay formulas isn't just about knowing the math; it's about understanding how these principles apply in our world. By following these tips, you can not only excel in academic settings but also apply these concepts practically in your day-to-day life, making you more adept at understanding and predicting the dynamics of various systems.
How do growth rates impact the outcome in financial investments?

+
Growth rates play a critical role in investments. A higher growth rate means your investment grows exponentially faster, but it also implies a higher risk. Conversely, a lower growth rate might result in smaller gains over time but offers more stability. Understanding the growth rate helps investors predict future value and make informed decisions on how to invest their money.
Why is continuous growth more accurate than discrete growth for some models?

+
Continuous growth assumes changes occur without interruption, which is more realistic for processes like natural population growth or chemical reactions. Discrete growth, where changes occur at fixed intervals, might not capture the nuanced fluctuations in time-dependent phenomena as effectively.
How can I apply growth and decay models to understand environmental issues?

+
Growth and decay models are useful for understanding environmental changes like pollution dispersal, the growth of invasive species, or the decay of pollutants over time. By applying these models, one can predict trends and develop strategies for mitigation or management of environmental challenges.