5 Tips for Mastering Slope and Y-Intercept Worksheets
Mathematics can sometimes feel like a daunting subject, especially when it comes to understanding the intricacies of algebra. One of the fundamental concepts in algebra that can pose challenges for many students is working with the slope and y-intercept of linear equations. These concepts are not only crucial for algebra but also form the bedrock for advanced studies in calculus, statistics, and beyond. In this comprehensive guide, we will explore five effective strategies for mastering slope and y-intercept worksheets, ensuring that both students and educators can approach these topics with confidence.
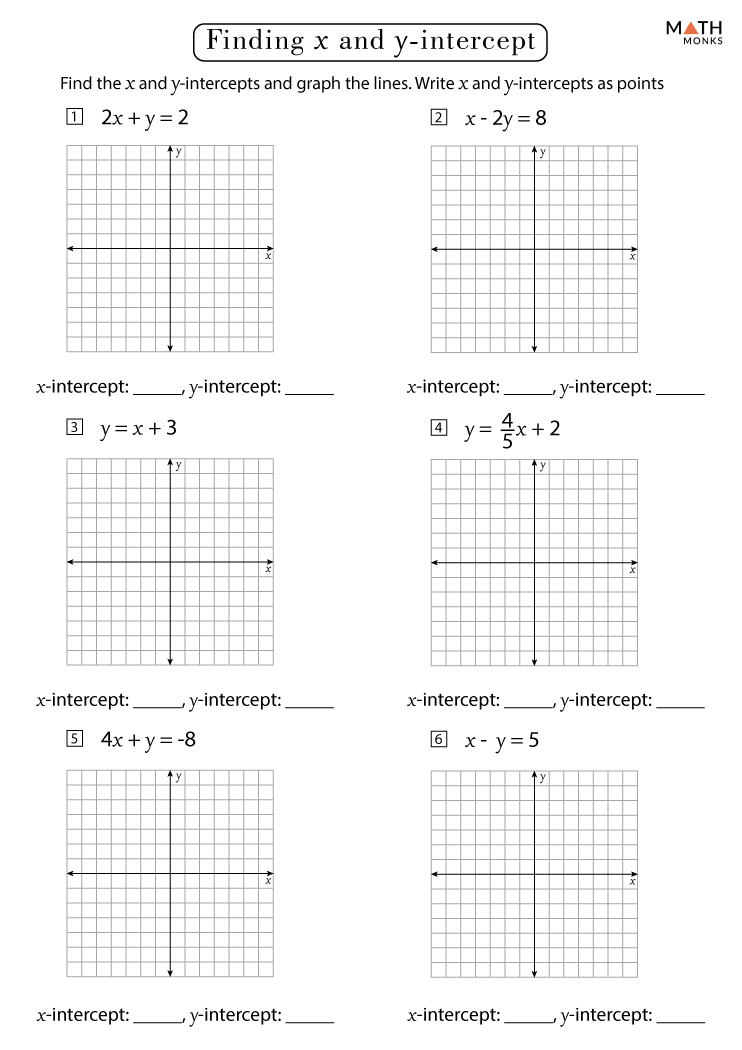
Understanding Slope and Y-Intercept

Before diving into the strategies, let's quickly review what slope and y-intercept signify:
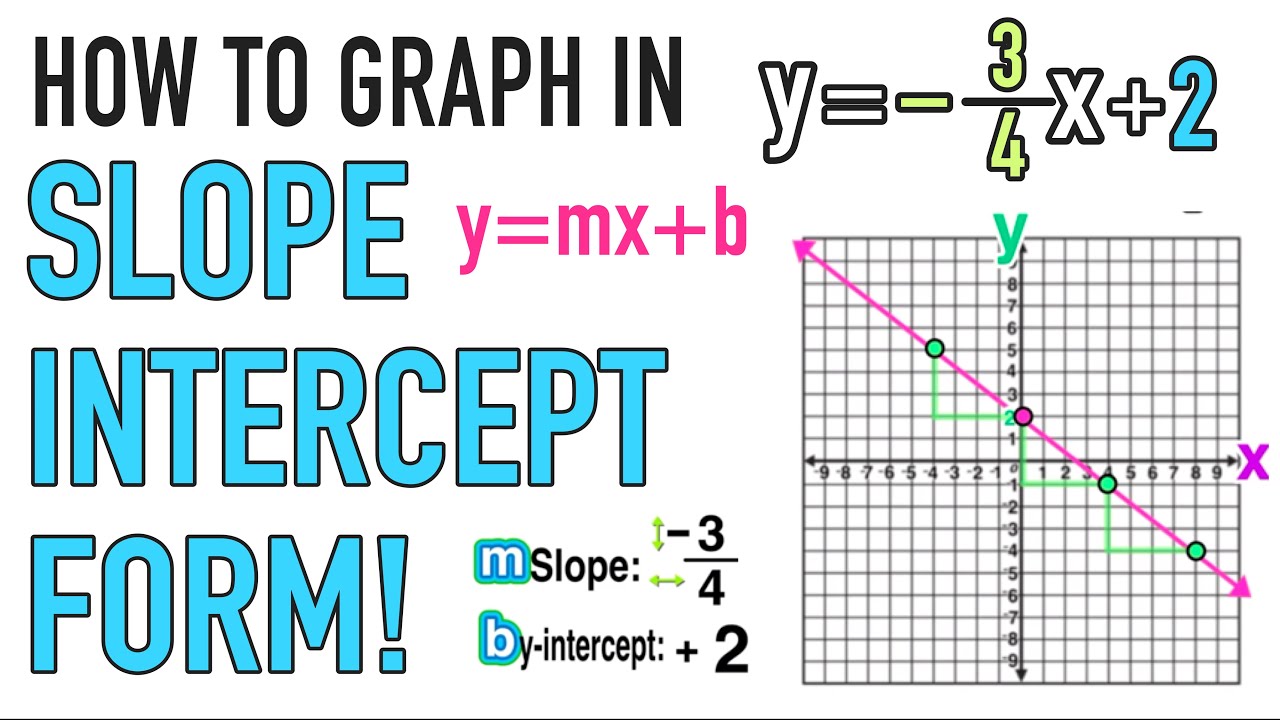
- Slope: The slope of a line measures its steepness and is defined as the change in y divided by the change in x (rise over run). Mathematically, it's represented as m in the equation y = mx + b.
- Y-Intercept: This is the point where the line intersects the y-axis, often represented as b in the same equation.

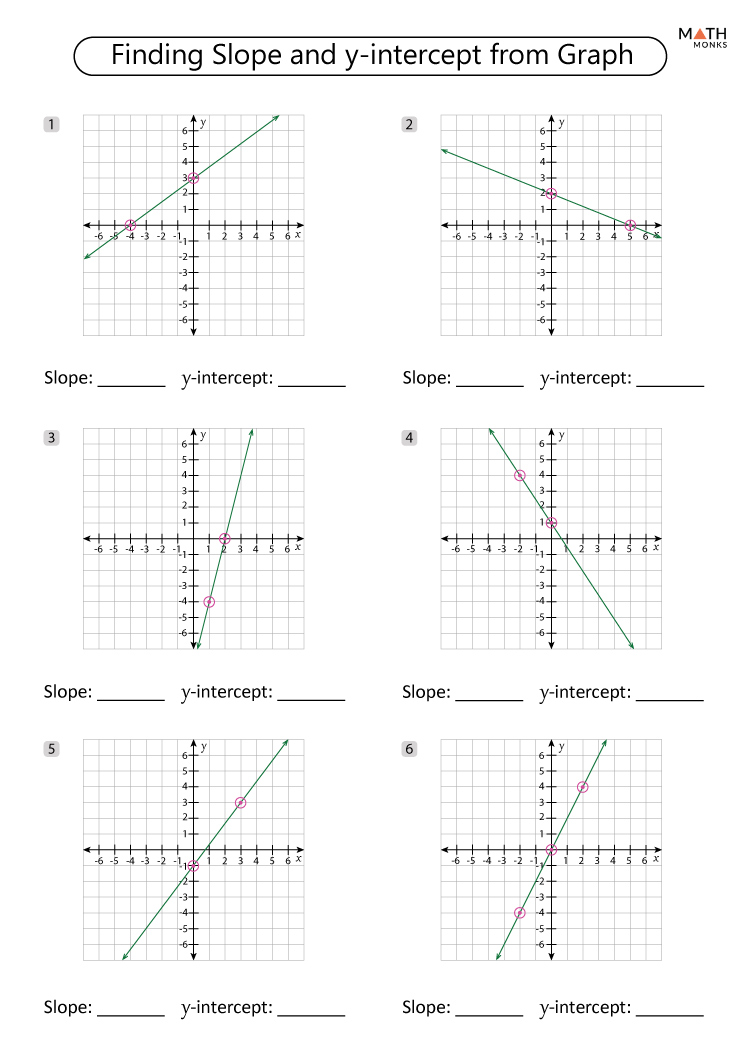
Tip #1: Visualize with Graphing

Graphing is one of the most powerful tools for understanding slope and y-intercept. Here's how you can use graphing effectively:
- Plot Points: Start by plotting a few points given by the equation to visualize where the line goes.
- Draw the Line: Connect these points to see the slope. A positive slope rises from left to right; a negative slope falls.
- Identify the Y-Intercept: Look where the line hits the y-axis. This is your y-intercept.
Tip #2: Use Real-Life Examples
Connecting math to real-life scenarios can make abstract concepts more tangible. Here are some examples:
- Ramp Slope: A wheelchair ramp must have a slope between 1:12 and 1:20. What does this mean in terms of rise over run?
- Rent vs. Utility Bills: Imagine your utility bill increases $5 for each additional unit of consumption. How does this relate to the slope of the line on a graph?
⚠️ Note: When using real-life examples, ensure they align closely with the mathematical concept to prevent confusion.
Tip #3: Practice with Repetition
The adage “practice makes perfect” holds true for algebra:
- Use worksheets with different types of problems to cover all aspects of slope and y-intercept.
- Engage with digital tools like graphing calculators or apps to visualize and adjust lines dynamically.
Tip #4: Utilize Mnemonics and Memory Aids

To remember formulas and concepts, try these:
- MIT (Match It to Intercept): When you see y = mx + b, think “Match the x-coefficient (m) to the y-intercept (b).” This mnemonic helps in identifying parts of the equation.
- Create visual cues or rhymes to remember how to calculate slope or find the y-intercept.
Tip #5: Engage in Group Study

Collaborative learning can greatly enhance understanding:
- Form study groups where each member explains a different problem or concept.
- Engage in peer teaching, where students teach each other; this reinforces understanding for both parties.
In wrapping up, mastering slope and y-intercept involves a blend of visualization, real-world application, repetitive practice, memory techniques, and social learning. These strategies not only help in understanding the foundational aspects of linear equations but also foster a deeper appreciation for the patterns and beauty in algebra. By employing these methods, students can transform what once seemed like an insurmountable task into a series of manageable steps towards mastering this crucial mathematical concept.
Why is the slope of a line important in real life?

+
The slope of a line has numerous applications in daily life. For example, it’s used in engineering to determine the pitch of roofs or the angle of ramps, in economics to understand cost functions, and in physics to describe motion or rate of change.
Can the y-intercept of a line be negative?

+
Yes, the y-intercept can be negative if the line intersects the y-axis below the origin. It simply means that when x is zero, the y-value is negative.
How can I remember which number is the slope and which is the y-intercept in the equation?

+
Use mnemonics like “Slope stands for Steepness, so it’s ’S’ for ’m’” or “B is below on the y-axis, thus ‘b’ is for y-intercept.”