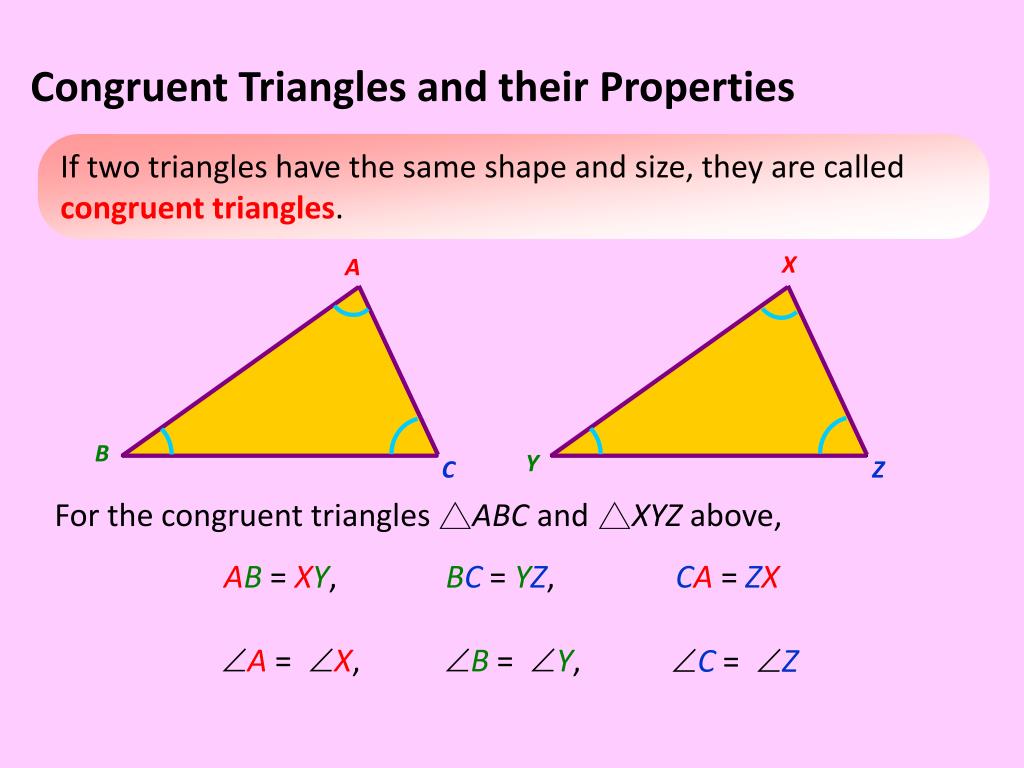
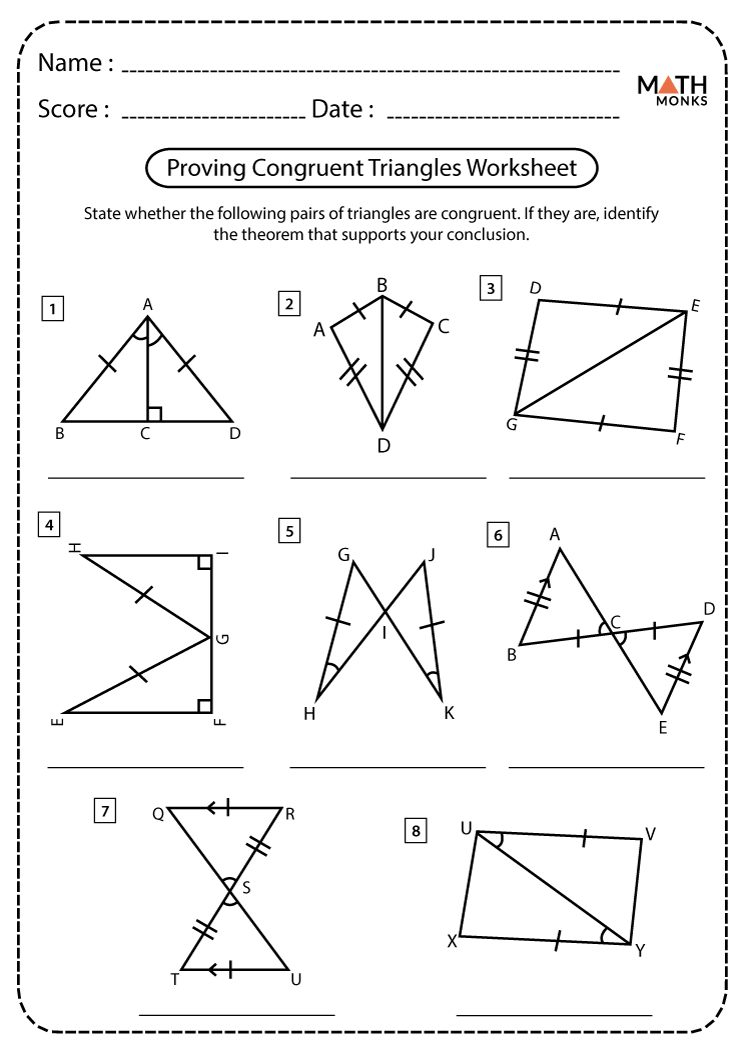
5 Ways to Prove Triangle Congruence Easily

Congruent triangles are a foundational concept in geometry, often used to solve complex proofs and understand the relationships between angles and sides. Proving that two triangles are congruent can be straightforward if you know the right methods. This blog post will walk you through five fundamental methods to prove triangle congruence:
1. Side-Side-Side (SSS) Congruence Postulate

The Side-Side-Side (SSS) congruence postulate is one of the simplest ways to prove triangles are congruent. Here's how it works:
- All three sides of the first triangle are congruent to all three sides of the second triangle.
This method relies on the fact that if the sides are equal, then the angles must fit perfectly to form two identical triangles. For example:
| Triangle ABC | Triangle DEF |
| AB = DE | BC = EF |
| AC = DF |
📝 Note: Remember that when proving congruence with SSS, you must have all three sides equal; otherwise, the method won't work.
2. Side-Angle-Side (SAS) Congruence Postulate

Side-Angle-Side (SAS) is another straightforward method where you use two sides and the included angle:
- One side and the angle adjacent to that side in one triangle are congruent to the corresponding side and angle in the other triangle.
This postulate is particularly useful when dealing with triangles where one side, or base, is given and the angle adjacent to this base is also known. For instance:

📝 Note: The angle must be the included angle between the two sides for SAS to work; if not, it's not sufficient for proving congruence.
3. Angle-Side-Angle (ASA) Congruence Theorem

When you have two angles and the side included between them, you can use the Angle-Side-Angle (ASA) theorem to prove congruence:
- Two angles and the side included between these angles are congruent to two corresponding angles and their included side in the other triangle.
This method is useful when you know the two non-included angles and the side between them. Here's how it looks:

📝 Note: Ensure the side is included between the angles for ASA congruence; otherwise, it doesn't hold.
4. Angle-Angle-Side (AAS) Congruence Theorem
Similar to ASA, but with a slight twist, the Angle-Angle-Side (AAS) theorem uses:
- Two angles and a non-included side that are congruent to two corresponding angles and a non-included side in the other triangle.
This theorem comes in handy when you have the measurement of two angles and one side, but not the side between the angles. For example:

5. Hypotenuse-Leg (HL) Congruence Theorem
Specifically for right triangles, the Hypotenuse-Leg (HL) theorem asserts:
- The hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle.
This theorem simplifies proving congruence for right triangles by focusing only on the hypotenuse and one of the legs:

📝 Note: HL theorem is exclusive to right triangles; don't use it for other types of triangles.
Understanding these methods not only helps in solving geometric proofs but also enhances your ability to visualize and understand the structure of triangles. By using these congruence postulates and theorems, you can confidently prove that two triangles are identical in shape and size, which is crucial for various applications in mathematics and beyond. Whether you're preparing for a geometry test or tackling real-world problems involving shapes, knowing how to prove triangle congruence is an invaluable skill.
Can I prove triangles congruent if I only know their angles?

+
No, knowing all three angles is not enough to prove triangles are congruent. You need information about at least one side, like in the ASA, AAS, or HL theorems.
What is the difference between similar and congruent triangles?

+
Similar triangles have the same shape but can differ in size. Congruent triangles, however, are identical in both shape and size.
Why are congruence theorems important?
+
Congruence theorems are essential because they provide the tools needed to prove relationships between triangles, leading to the solution of complex geometric problems.



