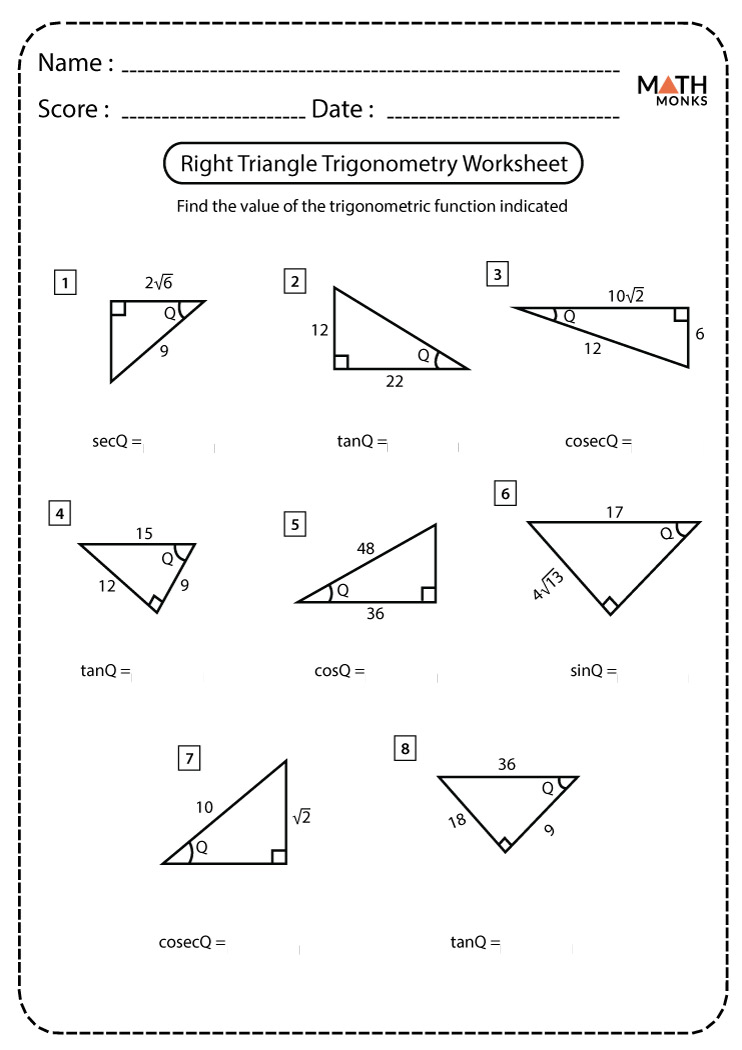
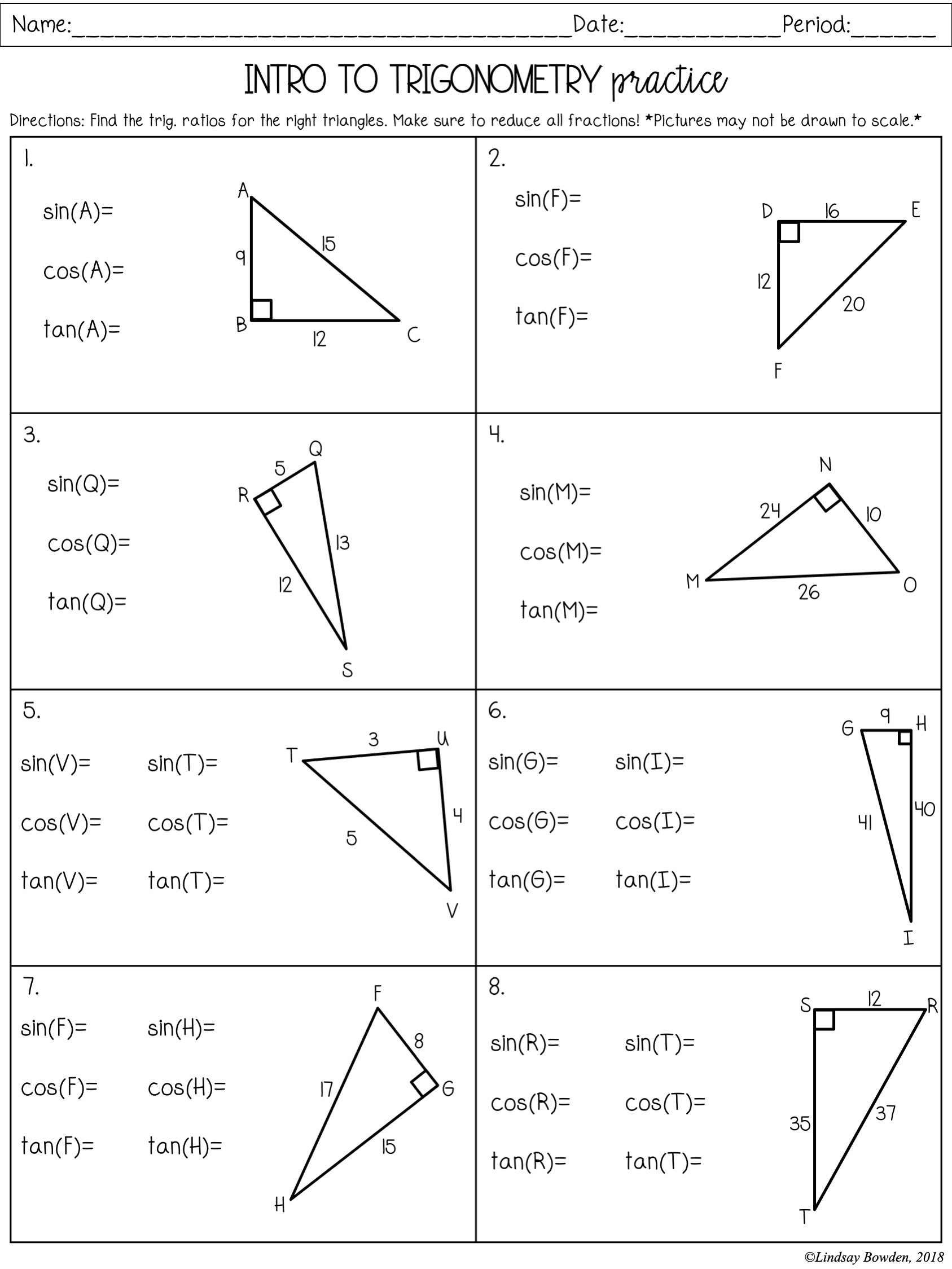
Right Triangle Trig Word Problems: Answer Key Revealed

Right triangle trigonometry is a vital branch of mathematics that finds applications in various fields like engineering, architecture, and physics. By understanding the relationships between the angles and sides of a right triangle, one can solve a myriad of real-world problems. Here's a deep dive into word problems involving right triangle trigonometry, complete with an answer key, to provide insight into how these mathematical principles work in practical scenarios.
Understanding Right Triangle Trigonometry


Before delving into the problems, it’s crucial to understand the three fundamental trigonometric ratios:
- Sine (sin): Opposite/Hypotenuse
- Cosine (cos): Adjacent/Hypotenuse
- Tangent (tan): Opposite/Adjacent
Solving Right Triangle Trigonometry Word Problems

Let’s look at some common scenarios:
Example 1: Height of a Building

From a point 50 feet away from the base of a building, the angle of elevation to the top of the building is 35 degrees. Calculate the height of the building.
| Given Information | Calculations |
|---|---|
| Distance from building (Adjacent side) | 50 feet |
| Angle of elevation (θ) | 35 degrees |
| Height to be found (Opposite side) | Use tan(θ) = Opposite / Adjacent |
| height = 50 * tan(35°) | ≈ 35.04 feet |
🌟 Note: Trigonometry functions like tan(θ) can be calculated using a calculator or trigonometry tables.
Example 2: Angle for Optimal Launch
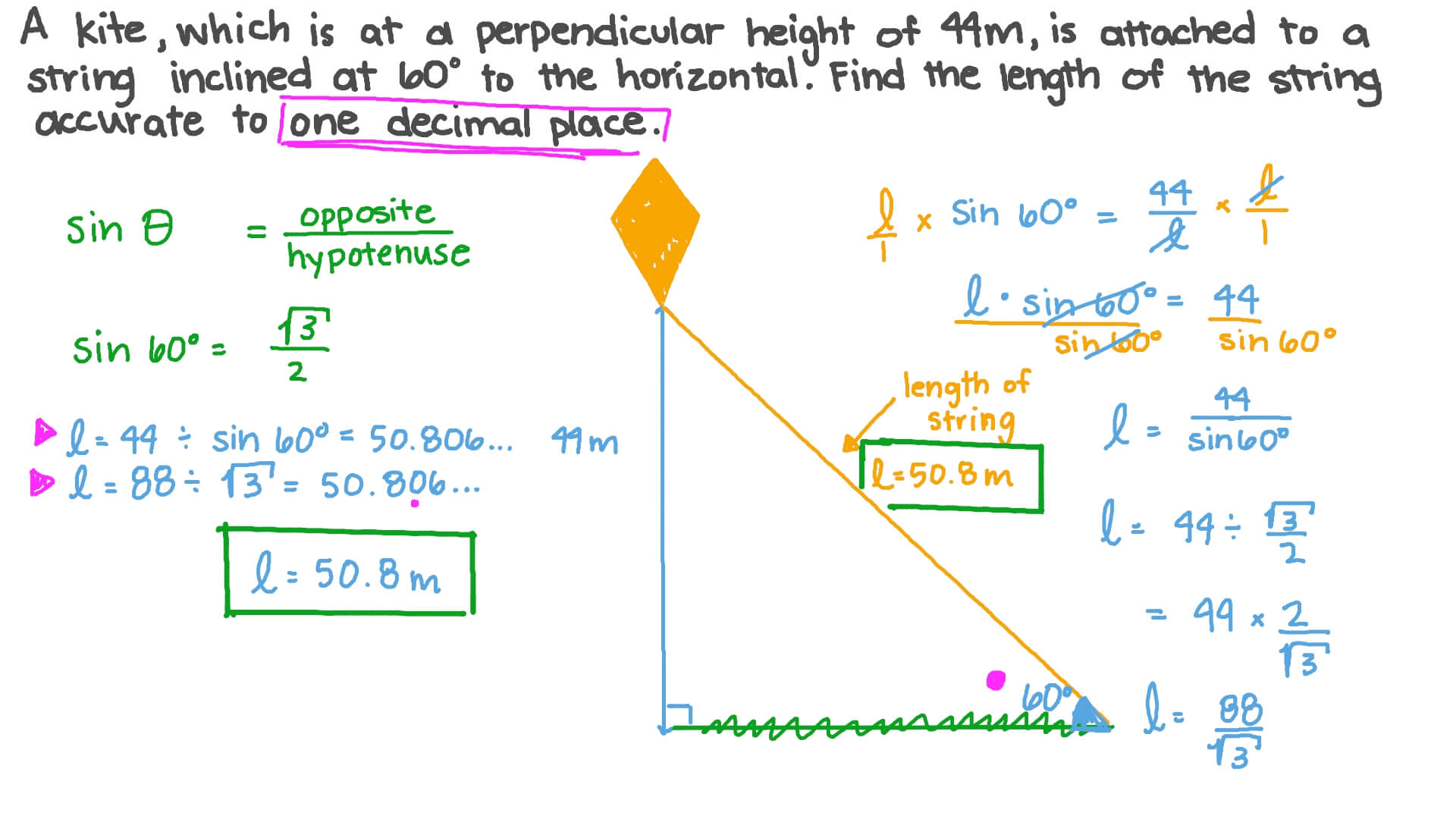
A water rocket needs to be launched at an angle to achieve a maximum height. If the length of the launch tube (the hypotenuse) is 2 meters, and the maximum height reached is 1.5 meters, what is the launch angle?
- Hypotenuse: 2 meters
- Maximum Height (Opposite): 1.5 meters
- Angle (θ): Use sin(θ) = Opposite / Hypotenuse
Sin(θ) = 1.5 / 2 = 0.75
Using the inverse sine function, θ ≈ 48.59°
Example 3: Distance to a Storm Cloud

From the ground, a radar station tracks a storm cloud. The angle of elevation to the cloud is 60 degrees, and the radar measures a straight-line distance to the cloud of 8 kilometers. How far away horizontally is the cloud from the station?
- Distance to Cloud (Hypotenuse): 8 km
- Angle of Elevation (θ): 60 degrees
- Horizontal Distance (Adjacent): Use cos(θ) = Adjacent / Hypotenuse
cos(60°) = Adjacent / 8
0.5 = Adjacent / 8
Adjacent = 8 * 0.5 = 4 km
Recap of Key Points

The examples provided illustrate the practical application of right triangle trigonometry. Whether it’s calculating building heights, optimal launch angles, or distances to objects, trigonometry plays a pivotal role. Here are some takeaways:
- Remember the three primary trigonometric functions: sine, cosine, and tangent.
- Identify the knowns and unknowns in your problem setup.
- Choose the appropriate trigonometric function based on the information provided.
- Use a calculator or trigonometric tables for precision in calculations.
What if the angle is not one of the standard angles?
+
If you’re dealing with angles that are not standard (like 30°, 45°, or 60°), you’ll use the exact values or approximate them using a calculator or trigonometric tables.
Can I use trigonometry for 3D objects?

+
Yes, trigonometry extends to 3D objects through principles like spherical trigonometry or by breaking down 3D shapes into right triangles.
Is trigonometry used in other areas of study?

+
Definitely! Trigonometry is integral in fields like surveying, navigation, acoustics, and more, where understanding angles and their relationships to distances is crucial.



