Master Slope Calculation: Graph Worksheet Guide

In the realm of mathematics and engineering, understanding slopes is crucial, especially when analyzing graphs and functions. A graph worksheet on slope calculation not only helps students and professionals master the basic and advanced concepts of slope but also integrates this knowledge into practical applications. This detailed guide will walk you through how to effectively use slope calculation worksheets, the importance of slopes in graph analysis, and tips for mastering the calculations.
Understanding Slope: The Foundation

Before delving into worksheet practice, let’s ensure we understand what slope means:
- Slope represents the steepness of a line or the rate of change between two points on a graph. It is calculated as the change in the y-coordinates divided by the change in the x-coordinates (rise over run).
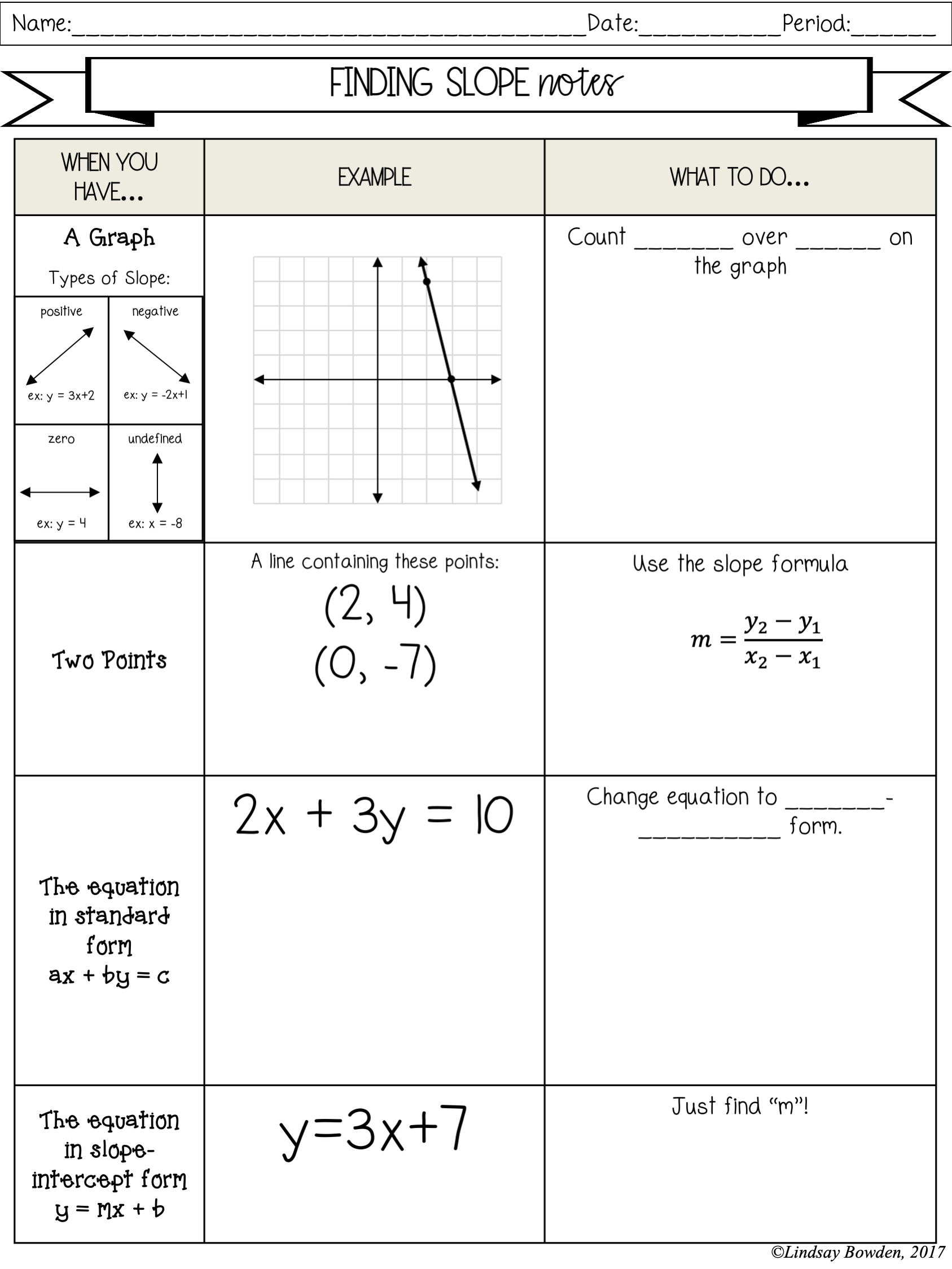
- The formula for calculating slope is: m = (y2 - y1) / (x2 - x1), where m is the slope, (x1, y1) and (x2, y2) are two points on the line.
- Slope can be positive, negative, zero, or undefined depending on the direction and nature of the line.
Using Slope Calculation Worksheets

Slope calculation worksheets are designed to:
- Help learners identify and calculate slopes from given points or line equations.
- Reinforce the concept through repetitive practice.
- Introduce variations in slope such as finding the slope of parallel or perpendicular lines.
Types of Questions in Slope Worksheets
Here are some common types of questions you might encounter:
- Identifying Slope from Points: Given two points on a graph, find the slope.
- Calculating Slope from Graph: Determine the slope by visual analysis of a line on a graph.
- Slope with Equation: Calculate the slope when given the linear equation in various forms like point-slope or slope-intercept.
- Real-World Applications: Problems where slope calculation relates to real-life scenarios, like ramp incline or grading.
How to Approach Slope Worksheet Problems

- Read the Problem Carefully: Understand what is being asked, whether it’s identifying the slope or calculating it using provided data.
- Label Points: When points are given, label them clearly on a graph or on your worksheet. For instance, label point A as (x1, y1) and point B as (x2, y2).
- Use the Slope Formula: Apply the slope formula mentioned above to calculate the slope.
- Check Your Work: If possible, plot the line on a graph to visually confirm the slope.
- Practice Variations: Try different scenarios, like finding slopes of parallel lines or slopes from real-life situations.
Tips for Mastering Slope Calculations

- Understand the Context: Knowing why you’re calculating slope can make it more intuitive. For example, in economics, slope might represent cost change per unit.
- Graph It Out: Sketching lines and plotting points can help solidify your understanding.
- Use Technology: Graphing calculators or software like Desmos can provide quick visual feedback on your calculations.
- Memorize Key Concepts: Zero slope, undefined slope, and slopes of parallel and perpendicular lines are essential to know.
- Worksheet Progression: Start with basic slope identification worksheets and move towards complex problems involving applications or algebraic manipulation.
✍️ Note: Practicing with a variety of slope calculation problems will improve your speed and accuracy in real-world applications.
Advanced Slope Topics

As you advance in your studies or applications:
- Explore tangent lines at a point on a curve, where the slope gives you the rate of change at that specific point.
- Understand how derivatives in calculus relate to the concept of slopes in differential geometry.
- Learn about the slope-intercept form and other forms of linear equations to deepen your grasp of how lines behave.
✍️ Note: The slope of a curve at any point isn't just about the rise over run; it's a cornerstone concept in calculus for understanding rates of change.
This guide aims to provide a comprehensive understanding and practical approach to mastering slope calculation through graph worksheets. By engaging with these resources, you'll not only enhance your mathematical prowess but also prepare yourself for various applications where slope analysis is pivotal. Whether you're tracking stock prices, designing buildings, or just plotting lines in geometry, your proficiency in calculating slopes will serve you well.
What does a zero slope mean?

+
A zero slope indicates a horizontal line where the y-coordinates of any two points are the same, implying no change in y for any change in x. Essentially, the rate of change is zero.
How do I find the slope if I only have one point?

+
To find the slope with one point, you need additional information such as the equation of the line or another point. If the line is horizontal or vertical, you can infer the slope from the point itself (e.g., for a vertical line through point (x, y), the slope is undefined).
Can you have a negative slope?

+
Yes, a negative slope means the line descends as you move from left to right on the graph. It implies a decrease in y-value for an increase in x-value.
Why is slope important in real-world applications?

+
Slope is critical in various fields:
- Engineering: For designing roads, ramps, and bridges where gradient is vital.
- Economics: Slope can represent cost, revenue, or profit per unit change.
- Physics: Slope relates to velocity or acceleration in motion graphs.
- Geography: Used to measure terrain steepness.
What’s the difference between a line’s slope and a curve’s slope at a point?
+
For a line, the slope is constant throughout its length. However, for a curve, the slope changes at each point. At any given point, the slope of a curve is represented by the tangent line at that point, which gives the instantaneous rate of change.



