5 Fun Ways to Solve Distance Problems with Pythagorean Theorem
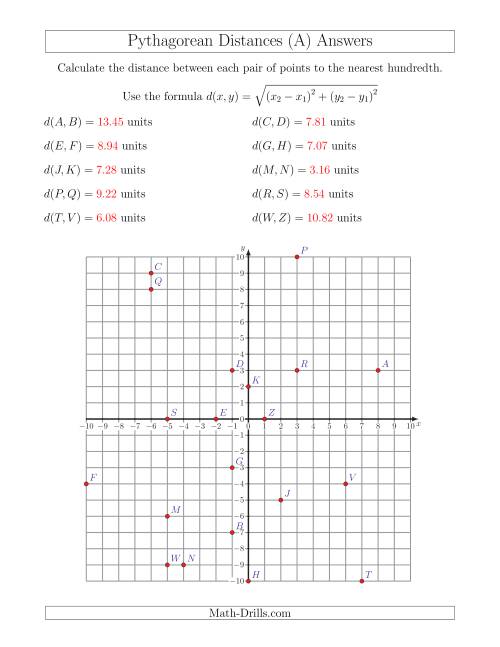
There's something magical about how numbers and shapes can represent and solve real-life scenarios. One of the classic tools in this mathematical spellbook is the Pythagorean Theorem. Known to many as "a squared plus b squared equals c squared" (a² + b² = c²), this theorem isn't just a staple of geometry class but also a versatile problem-solving tool. Whether you're laying out your garden, planning your next hike, or simply want to impress your friends with your mathematical prowess, the Pythagorean Theorem can be your secret weapon. Let's dive into five engaging and fun ways to use this theorem to solve distance problems.
1. The Treasure Map Adventure


Imagine you're on a treasure hunt. Your map provides you with two clues: from Point A, you need to walk north 200 meters to a big oak tree, then turn and walk east 150 meters to the treasure spot. How far is the treasure directly from Point A?
- Step 1: Identify the legs of the right triangle - the north and east distances.
- Step 2: Use the theorem: c = √(200² + 150²)
- Step 3: Calculate the result: c ≈ 250 meters
💡 Note: Always check your calculations and consider the scale of your map for precision.
2. The Garden Plot Scheme
If you're planning a garden, you might want to lay out a path that crosses diagonally from one corner to the opposite one. Here’s how to find this shortest path:
- First, measure the length and width of the rectangular garden.
- Let's say the garden is 30 feet by 40 feet.
- Use the theorem: d = √(30² + 40²)
- Calculate: d ≈ 50 feet
| Measurement | Value (feet) |
|---|---|
| Length | 40 |
| Width | 30 |
| Diagonal (d) | ≈50 |
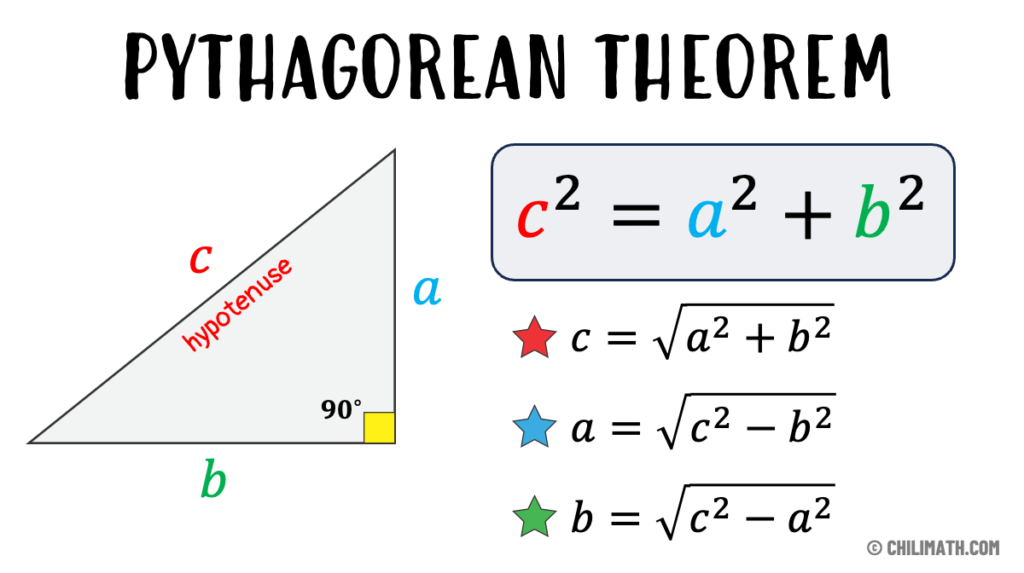
3. The Towering Heights
How tall is a building or tree when you can't measure it directly? Using the Pythagorean Theorem, here's how to estimate it:
- Measure the distance from the base of the tree to a point where you can see the top of the tree (call this distance 'd').
- Stand at that point and measure the angle to the top of the tree using a clinometer or app.
- Use tan(θ) = height / distance to the tree, where θ is your angle measurement.
- Height = distance × tan(θ)
👟 Note: Ensure the ground is flat, and take multiple readings for accuracy.
4. The Outdoor Hike

When hiking through hills or valleys, knowing how much ground you've covered can be a fun application of geometry. Let's say you hike 500 meters up a hill at a 20-degree angle:
- Determine the horizontal distance traveled.
- Using trigonometric functions (but fundamentally rooted in the Pythagorean Theorem), horizontal distance = vertical distance / tan(20°)
- Now, use the theorem to find the direct distance (c) from starting point to endpoint.
5. Playing Ball on a Sloped Field

When playing ball sports on a sloped field, the Pythagorean Theorem can help calculate how much further you might throw or hit the ball:
- Estimate the slope or angle of the field.
- Consider the horizontal distance of the throw or hit.
- Use the theorem to calculate the actual distance considering the slope's vertical component.
Using the Pythagorean Theorem in such playful and practical ways not only sharpens your math skills but also makes everyday tasks and games more interesting and enjoyable. The fun lies in understanding how geometry, particularly the Pythagorean Theorem, intertwines with our environment, making life not just a numbers game but a fascinating journey through shapes and distances.
Why is the Pythagorean Theorem useful for distance calculations?

+
The Pythagorean Theorem provides a direct method to calculate the shortest distance between two points in a right triangle, which often represents distances in real-world scenarios where you can’t move in a straight line.
Can the Pythagorean Theorem be used with any triangle?

+
It’s specifically applicable to right triangles, but with other geometric tools like the Law of Cosines, you can use it to solve distances in any triangle indirectly.
How accurate is this method for practical measurements?

+
Accuracy depends on how precisely you can measure distances and angles. For practical applications, it can be very accurate with good measurements.



