5 Algebra Hacks to Prove Parallel Lines Fast
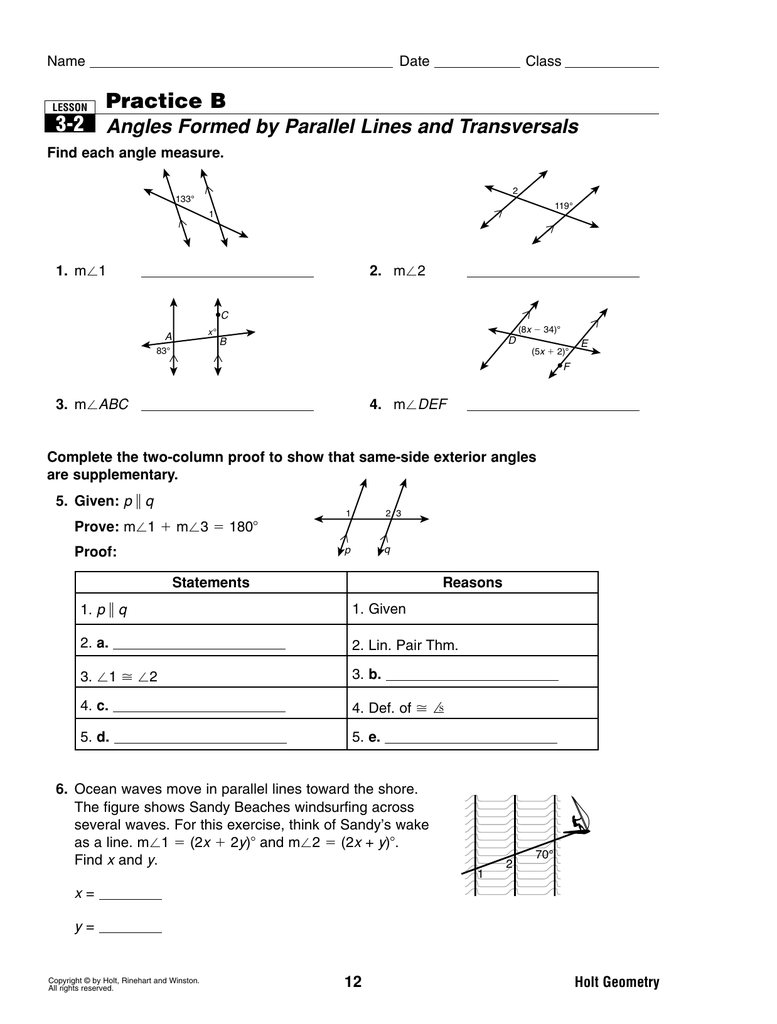
When it comes to geometry, proving that lines are parallel can sometimes feel like a complex puzzle. But with the right algebra tricks and theorems, this task can become straightforward and fast. Here are five algebra hacks to help you quickly prove that lines are parallel.
1. Using Slope Formula

One of the most straightforward methods to check if two lines are parallel is to compare their slopes. If two lines have the same slope, they are parallel. Here’s how you can do it:
- Find the slope of each line using the slope formula: m = (y2 - y1) / (x2 - x1).
- Compare these slopes. If they are identical, the lines are parallel.
Example: Consider lines L1 passing through points (1,2) and (3,4) and L2 through (0,3) and (4,9). Calculate the slopes:
- For L1: Slope = (4 - 2) / (3 - 1) = 1
- For L2: Slope = (9 - 3) / (4 - 0) = 3⁄2
2. Leveraging the Transversal Theorem
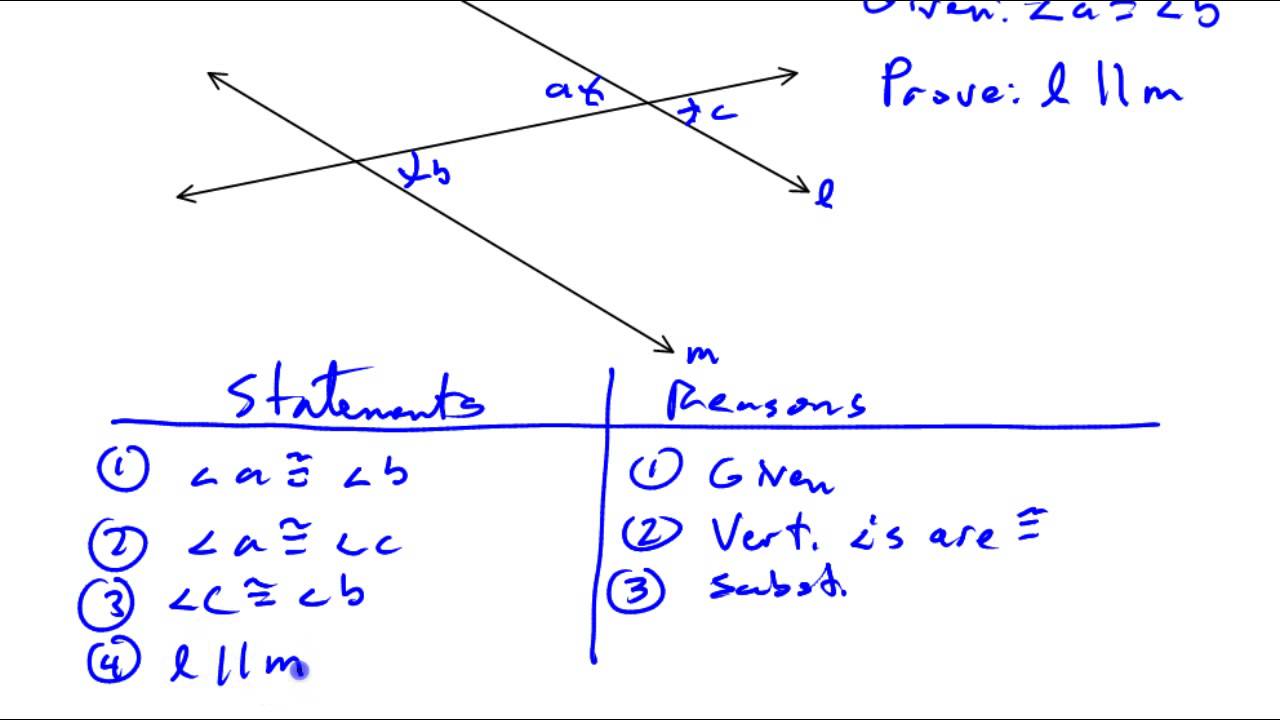
If two lines are cut by a transversal, and the interior or exterior angles on the same side are supplementary (sum to 180 degrees), then the lines are parallel. Here’s what to do:
- Identify two angles on the same side of the transversal that sum to 180°.
- If you can prove this relationship, the lines are parallel.
Example: Suppose you have lines L1 and L2 intersected by transversal T. If ∠1 and ∠2, which are corresponding angles, have measures 60° and 120° respectively, proving that L1 and L2 are parallel.
3. Angle Chasing with Algebra

Often in geometric proofs, you can find parallel lines by setting up and solving algebraic equations for angles. This method uses:
- The fact that corresponding angles, alternate interior angles, or vertical angles are equal when lines are parallel.
- Using algebra to show that these angles are indeed equal or supplementary.
Example: Assume lines a and b are intersected by a transversal, and we know:
- ∠A = 4x + 30°
- ∠B = 2x + 50°
- 4x + 30 = 2x + 50
- 2x = 20
- x = 10
💡 Note: Remember, the sum of angles on a straight line is 180°, which can be useful for setting up equations.
4. The Converse of Corresponding Angles Postulate

The converse states that if corresponding angles are equal, then the lines are parallel. Here’s how to apply it:
- Find two corresponding angles formed by the transversal.
- If these angles are equal, use algebra to prove this, confirming parallelism.
5. The Coordinate Geometry Approach
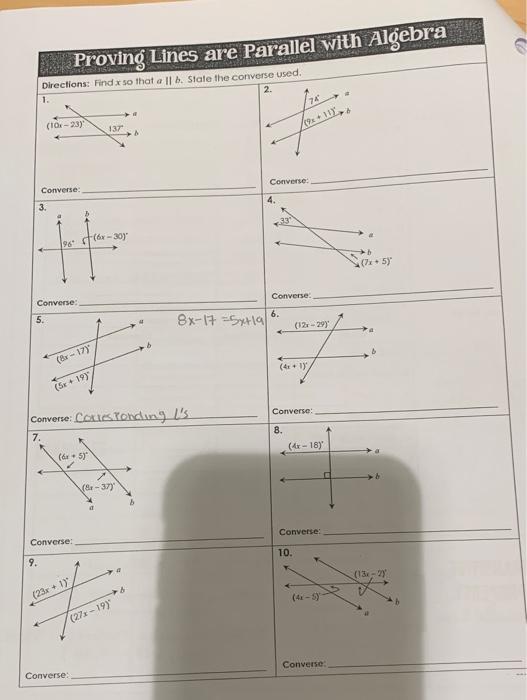
By plotting the given points and lines on a coordinate plane, you can utilize algebra to show parallelism:
- Plot the points that define the lines.
- Use the equation of a line (y = mx + b) to determine if the lines share the same slope (m).
| Line Equation | Slope |
|---|---|
| y = 2x + 5 | 2 |
| y = 2x + 3 | 2 |

Since the slopes are equal, these lines are parallel.
Understanding how to use algebra for geometric proofs can significantly streamline your work in mathematics. By mastering these five algebra hacks, you can approach proofs of parallelism with confidence and ease. These techniques not only save time but also deepen your understanding of the intrinsic relationship between algebra and geometry. Next time you're faced with proving lines are parallel, these methods will serve as your trusty tools.
Why is slope important when proving lines are parallel?

+
Slope is crucial because if two lines have the same slope, they either coincide or are parallel. This allows us to use algebra for geometric proofs without needing to measure angles directly.
Can I prove parallelism without knowing specific points?

+
Yes, you can use geometric theorems like the converse of the corresponding angles postulate or algebraic equations derived from known angles to prove parallelism without specific point coordinates.
How does the transversal theorem help in proving parallel lines?

+
The transversal theorem provides a straightforward way to prove parallelism if you know that angles on the same side of the transversal are supplementary. This simplifies algebraic calculations when angle measures are known.



