Multiplying Polynomials Coloring Worksheet Answer Key Revealed

An Introduction to Multiplying Polynomials

Multiplying polynomials is a fundamental algebraic operation that plays a crucial role in more advanced mathematical topics like calculus, linear algebra, and even in real-world applications like engineering and computer science. This post will guide you through understanding the multiplication of polynomials step-by-step, demystifying the process and revealing the key to mastering this essential algebra skill.

What are Polynomials?

Before diving into multiplication, let’s clarify what polynomials are:
- Definition: A polynomial is an expression consisting of variables (or indeterminates) and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation.
- Examples:
- 3x2 + 5x - 2
- 7x3 + 6x + 9
Understanding Multiplication

Multiplying polynomials essentially means combining like terms after the distribution of terms over addition:
- Distribute each term in one polynomial to each term in another.
- Combine the resulting products by adding like terms.
Step-by-Step Multiplication Example

Here’s an example where we multiply (3x + 2) and (x - 4):
- Step 1: Distribute 3x to each term in (x - 4):
- 3x * x = 3x2
- 3x * (-4) = -12x
- Step 2: Distribute 2 to each term in (x - 4):
- 2 * x = 2x
- 2 * (-4) = -8
- Step 3: Combine the results:
- 3x2 + (-12x) + 2x + (-8)
- Simplify to: 3x2 - 10x - 8
⚠️ Note: When combining like terms, always ensure you add/subtract terms with the same exponent.
Visual Aid: Coloring Worksheet

To make this process visual, consider a coloring worksheet where students match the colors of matching terms:
| Problem | Color Key |
|---|---|
| (3x + 2)(x - 4) |
|

Revealing the Answer Key
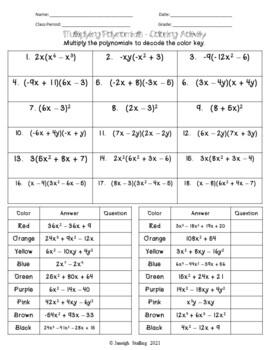
After working through various problems, here is how the answer key might look for the polynomial multiplication:
| Original Problem | Multiplied Polynomials |
|---|---|
| (3x + 2)(x - 4) | 3x2 - 10x - 8 |
| (2y + 3)(4y - 1) | 8y2 + 10y - 3 |
🌟 Note: The answer key helps in checking your work but remember, understanding the process is crucial for exam preparation and higher mathematics.
By understanding the steps and visual representation, students can quickly identify their mistakes and refine their skills in polynomial multiplication. This method not only simplifies learning but also makes it engaging through the use of colors and visual aids.
Remember, mastering polynomial multiplication involves:
- Distributing each term properly.
- Combining like terms efficiently.
- Using visual aids for better understanding and memory retention.
With practice, you’ll find that polynomials can be quite manageable and even fun to work with. Use worksheets, like the ones mentioned, to practice and reinforce your understanding of this fundamental algebraic operation.
In wrapping up this journey through polynomial multiplication, keep in mind that the key to algebraic success lies in understanding the mechanics behind these operations. Not only does it make higher-level math more accessible, but it also boosts problem-solving abilities, which are useful in numerous fields.
Why is understanding polynomial multiplication important?

+
Understanding polynomial multiplication is essential because it’s foundational for advanced mathematics like calculus, where you deal with derivatives and integrals of polynomials. It’s also crucial in fields like computer graphics for curve and surface modeling.
What are common mistakes students make when multiplying polynomials?

+
Common errors include forgetting to distribute each term, misunderstanding the sign of terms during distribution, and failing to combine like terms correctly. Another frequent mistake is not distributing across the whole polynomial when there are multiple terms in the parentheses.
Can you recommend any tools for practicing polynomial multiplication?

+
There are several online math platforms like Khan Academy, Wolfram Alpha, or even educational apps like Photomath which provide interactive lessons and practice problems. Additionally, physical worksheets with visual aids, like the one discussed, can significantly help.