Central Angles and Arc Measures: Answer Key Revealed

In the realm of geometry, central angles and arc measures play pivotal roles in understanding the circle's intrinsic properties. Whether you're a student grappling with trigonometry or a professional in engineering, mastering the relationship between central angles and arc measures can unlock many analytical doors. Let's dive into the crux of these geometric concepts, exploring how they interact, how they're calculated, and how they apply in real-world scenarios.
Understanding Central Angles

Definition: A central angle is an angle whose vertex is the center of a circle, and whose sides are radii of the circle. Central angles can be measured in degrees or radians, and they are essential in determining the arc length or area of a sector of a circle.
Key Concepts:
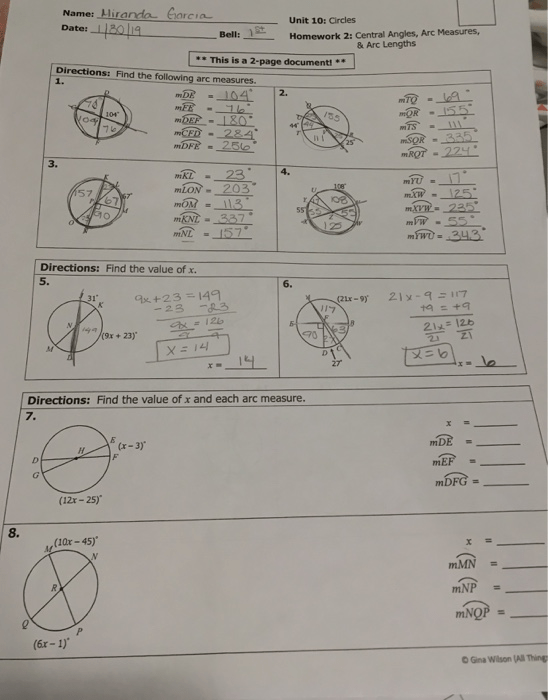
- Measure: The measure of a central angle is typically denoted by θ (theta). It’s the angle subtended by two radii at the center.
- Arc Length: The arc length associated with the central angle is calculated using the formula Arc length = θ/360° × 2πr, where θ is in degrees and r is the radius of the circle.
Calculating Central Angles:

- If you know the arc length and the radius of the circle, you can solve for the central angle using the inverse of the arc length formula:
- θ = (Arc length × 360°) / (2πr)
Arc Measures Explained

Definition: An arc of a circle is any connected part of the circle. An arc is measured either by the central angle that intercepts it or by its length along the circumference.
Types of Arcs:

- Major Arc: The arc greater than 180°, which implies a central angle greater than 180°.
- Minor Arc: The arc less than or equal to 180°, with a corresponding central angle.
- Semicircle: An arc exactly 180°.
Calculating Arc Length:

- The length of an arc is given by the formula Arc length = (θ/360°) × 2πr, where θ is the measure of the central angle in degrees.
Relationship Between Central Angles and Arc Measures

The relationship between the central angle and the arc measure is straightforward when you understand that:
- An arc's measure in degrees is always equal to the measure of the central angle that intercepts it.
- The length of the arc is proportional to the degree measure of the central angle relative to the whole circle.
Application in Real Life:

- Architecture: Arches in buildings can be designed using central angle properties to distribute load evenly or for aesthetic design.
- Machinery: Calculating angles for gears, cogs, and cams involves understanding arc measures.
- Astronomy: Determining the position of stars or planets involves dealing with angles and arcs.
Steps to Solve Problems with Central Angles and Arcs

- Identify the Given: Determine what is known, such as radius, arc length, or central angle.
- Use Formulas: Apply the appropriate formula to find what's missing:
- To find arc length given the central angle and radius: Arc length = (θ/360°) × 2πr
- To find the central angle given the arc length and radius: θ = (Arc length × 360°) / (2πr)
- Check Units: Ensure the angle measurement is in degrees or radians as needed.
- Interpret: Consider how the answers relate to the context of the problem or real-life applications.
✅ Note: Always double-check your units when calculating arcs and angles, as using radians or degrees incorrectly can lead to significant errors.
In summary, the exploration of central angles and arc measures not only enhances our understanding of circular geometry but also finds practical applications in various fields. From designing machinery to plotting celestial bodies, these principles are foundational. The key to mastering these concepts lies in understanding the relationships and using the right formulas to solve problems efficiently.
What is the difference between a minor and a major arc?

+
A minor arc is an arc whose measure is less than or equal to 180°, while a major arc spans more than 180°. The central angle for a minor arc is also less than or equal to 180°.
How do you convert between arc length and central angle measure?

+
To convert between arc length and central angle measure, use the formula: θ = (Arc length × 360°) / (2πr) for finding the central angle, and Arc length = (θ/360°) × 2πr to find the arc length.
Why is it important to know the radius when dealing with arc measures?

+
The radius is crucial because both the arc length and the central angle are directly proportional to the radius of the circle. Without knowing the radius, you cannot accurately calculate arc lengths or the angles subtended by those arcs.