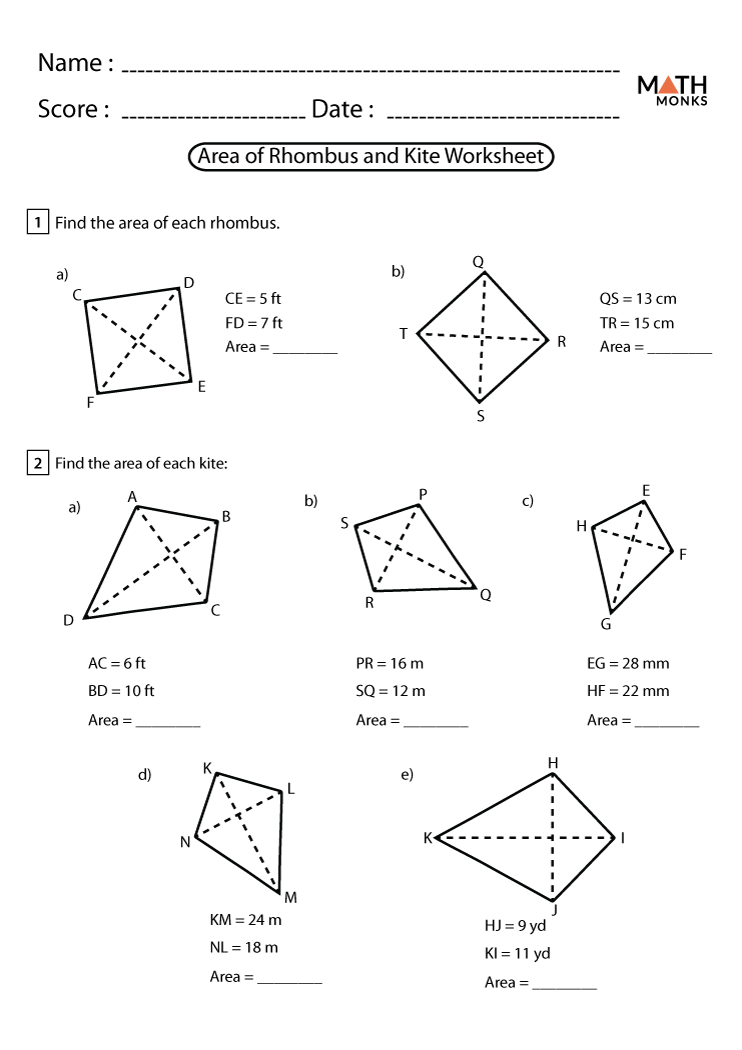
5 Key Properties of Rhombi You Should Know

When it comes to geometric shapes, few are as intriguing and symmetric as the rhombus. A rhombus, often referred to as a diamond or a lozenge, is a type of quadrilateral where all four sides are of equal length. However, rhombi are not just about their aesthetic appeal; they exhibit several key mathematical properties that make them useful in various fields from design to engineering. Here are five essential properties of rhombi that you should know:
Equal Side Lengths


The most defining feature of a rhombus is that all four sides are congruent. This symmetry gives the rhombus its characteristic diamond shape, making it instantly recognizable. This equality in side lengths means that:
- A rhombus can also be classified as a parallelogram, but not all parallelograms are rhombi.
- By rotating a rhombus, you’ll always see the same shape from different angles, which is not the case with most other quadrilaterals.
Opposite Angles are Equal


In addition to having equal sides, a rhombus has the property that:
- Opposite angles are congruent. This means if one angle measures 40 degrees, then the opposite angle will also measure 40 degrees.
- While opposite angles are equal, adjacent angles sum up to 180 degrees, mirroring the properties of a parallelogram.
Diagonals Bisect Each Other at 90 Degrees


The diagonals of a rhombus:
- Bisect each other at right angles. This feature makes rhombi particularly useful in design, architecture, and engineering where exact right-angle intersections are required.
- The point where the diagonals intersect is equidistant from all four vertices, creating four right-angled triangles within the rhombus.
Diagonals Divide the Rhombus into Two Pairs of Congruent Triangles
The diagonals of a rhombus:
- Not only bisect each other but also divide the rhombus into two congruent pairs of isosceles triangles.
- This property is visually demonstrated when you draw the diagonals:
| Triangle Properties | Before Diagonals | After Diagonals |
|---|---|---|
| Equal Sides | None | Two per Triangle |
| Congruency | No | Two Pairs |

🔍 Note: The congruent triangles formed by the diagonals are also right-angled due to the 90-degree intersection of the diagonals.
Symmetry and Rotational Symmetry


The symmetry of a rhombus:
- Has two lines of symmetry, one for each diagonal, dividing it into symmetrical halves.
- It also exhibits rotational symmetry of order 2, meaning it looks the same after a 180-degree rotation.
In summary, rhombi are not just visually appealing but also carry several mathematical properties that make them unique. Their equal side lengths, opposite angles, and diagonal characteristics contribute to their utility in various applications, from solving complex geometrical problems to designing structures and logos.
What is the difference between a rhombus and a square?

+
A square is a special type of rhombus where all four angles are right angles (90 degrees). While a rhombus has equal sides, it does not necessarily have all angles as 90 degrees, making a square a subtype of rhombus.
Can a rhombus be a rectangle?

+
Technically, yes, but only if all the angles of the rhombus are 90 degrees, making it a square, which is also a rectangle.
Are the diagonals of a rhombus always equal in length?

+
No, the diagonals of a rhombus are not always equal in length. However, they always intersect at 90 degrees, bisect each other, and divide the rhombus into two congruent pairs of triangles.
How can I recognize a rhombus in real life?

+
Look for objects or signs with four sides of equal length but not necessarily right angles. Common examples include diamond shapes on playing cards, jewelry settings, and signage.
Why is the diagonal property of rhombi useful?

+
The diagonal property of rhombi where they bisect at 90 degrees is particularly useful in design and engineering to ensure structural integrity, symmetry, and aesthetic appeal in buildings, kites, or geometric patterns.