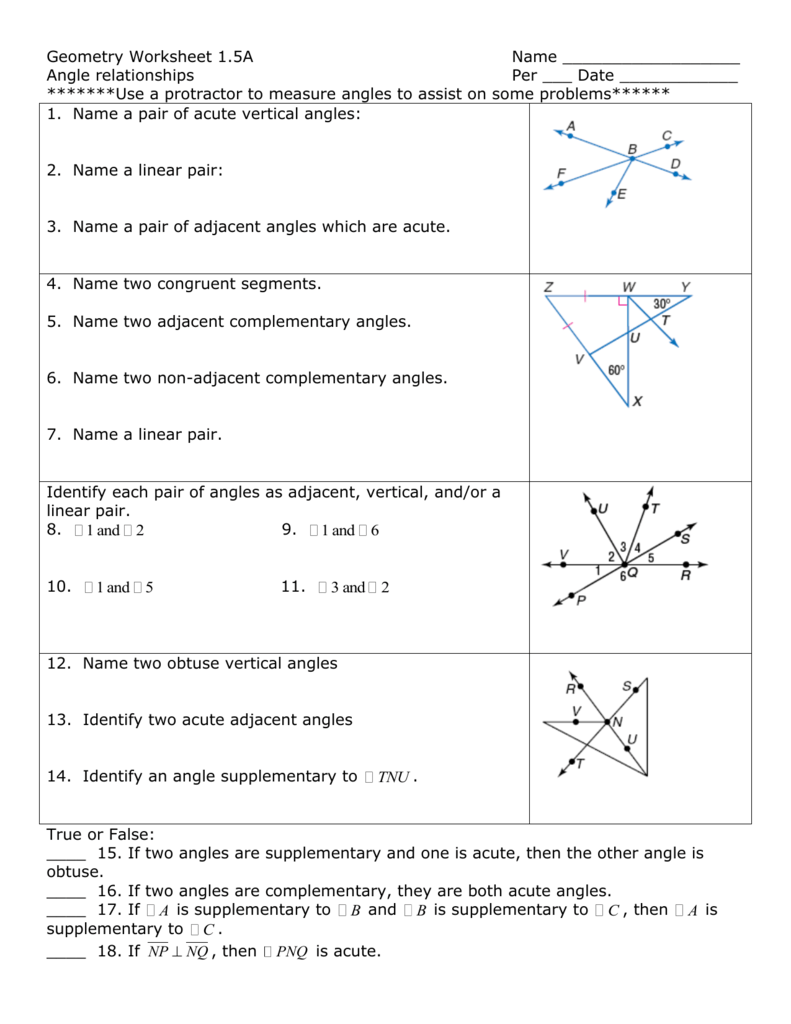
Angle Relationships Puzzle Worksheet Solutions Revealed

In the world of geometry, understanding the intricate web of relationships between angles is not just a key to solving complex puzzles but also to mastering this branch of mathematics. This blog post aims to guide you through the labyrinth of angle relationships, offering insights and strategies to conquer any geometry worksheet you come across. Whether you're a student looking to ace your math class or a tutor seeking better ways to explain angle relationships, this comprehensive guide is for you.
Understanding the Basics of Angle Relationships


Angles are formed whenever two lines intersect, and their relationships can be categorized into several types:
- Adjacent Angles - Angles that share a vertex and a common side.
- Vertical Angles - Opposite angles formed by the intersection of two lines, which are always equal in measure.
- Complementary Angles - Two angles whose measures add up to 90 degrees.
- Supplementary Angles - Two angles whose measures add up to 180 degrees.
- Linear Pair - Adjacent angles that are supplementary.
🔍 Note: Remember, angle relationships can often be identified by their position relative to the intersecting lines.
Solving Angle Puzzles with Formulas and Strategies


Let’s delve into some common problems you might encounter:
Solving for Angles Using Vertical Angles

If you know the measure of one angle in a set of vertical angles, you can determine the measure of the other by understanding that they are equal:
Angle A = Angle C and Angle B = Angle D
- If Angle A is 50 degrees, then Angle C is also 50 degrees.
- Similarly, if you know Angle B, you can find Angle D.
Complementary and Supplementary Angles

When you need to find the measure of an angle that is part of a complementary or supplementary pair:
- If Angle X is complementary to Angle Y, and Angle X measures 40 degrees, then Angle Y would be:
- And for supplementary angles, if Angle Z measures 130 degrees:
Angle Y = 90 - Angle X
Supplementary Angle = 180 - Angle Z
Using Linear Pair for Problem Solving
The linear pair property states that adjacent angles along a straight line sum up to 180 degrees. If you know one of the angles:
Angle A + Angle B = 180 degrees
Case Studies: Real-World Application of Angle Relationships


Angles are not just theoretical constructs; they have practical applications in everyday life:
- Architecture - Architects use angle relationships to design buildings, ensuring structural integrity and aesthetic appeal.
- Engineering - Mechanical engineers calculate angles for gears, pulleys, and lever systems.
- Art and Design - Artists apply principles of angles to create visually appealing compositions.
🔍 Note: Practical applications often involve not just one type of angle relationship but a combination of several to solve real-world problems.
Advanced Angle Relationships: Interior and Exterior Angles


When dealing with polygons, understanding interior and exterior angles becomes crucial:
Interior Angles

The sum of the interior angles of a polygon can be found using the formula:
Sum of Interior Angles = (n - 2) * 180 degrees
- Where n is the number of sides of the polygon.
Exterior Angles

Each exterior angle of a regular polygon can be calculated with:
Exterior Angle = 360 degrees / n
🔍 Note: Remember, the sum of exterior angles of any polygon is always 360 degrees.
Wrapping Up Angle Relationships

In conclusion, understanding angle relationships is a fundamental aspect of geometry. By mastering the basics like vertical, complementary, and supplementary angles, you unlock the key to tackling more complex geometric problems. We’ve explored practical strategies for problem-solving and how these principles apply to real-world scenarios, from architecture to engineering. The ability to visualize and apply these relationships not only enhances problem-solving skills but also enriches one’s spatial reasoning and logical thinking. Remember, like any skill, mastering angle relationships requires practice. Keep solving, keep learning, and watch as your geometric prowess grows.
What is the difference between adjacent and vertical angles?
+
Adjacent angles share a common vertex and a side, while vertical angles are opposite each other when two lines intersect, and they are always equal in measure.
Can all angles be solved using a single type of angle relationship?

+
No, often solving for angles requires understanding multiple relationships and applying several strategies simultaneously.
How do real-world applications benefit from understanding angle relationships?

+
Real-world applications like architecture, engineering, and art benefit from understanding angle relationships as they help in designing structures, optimizing mechanics, and creating visually balanced compositions.