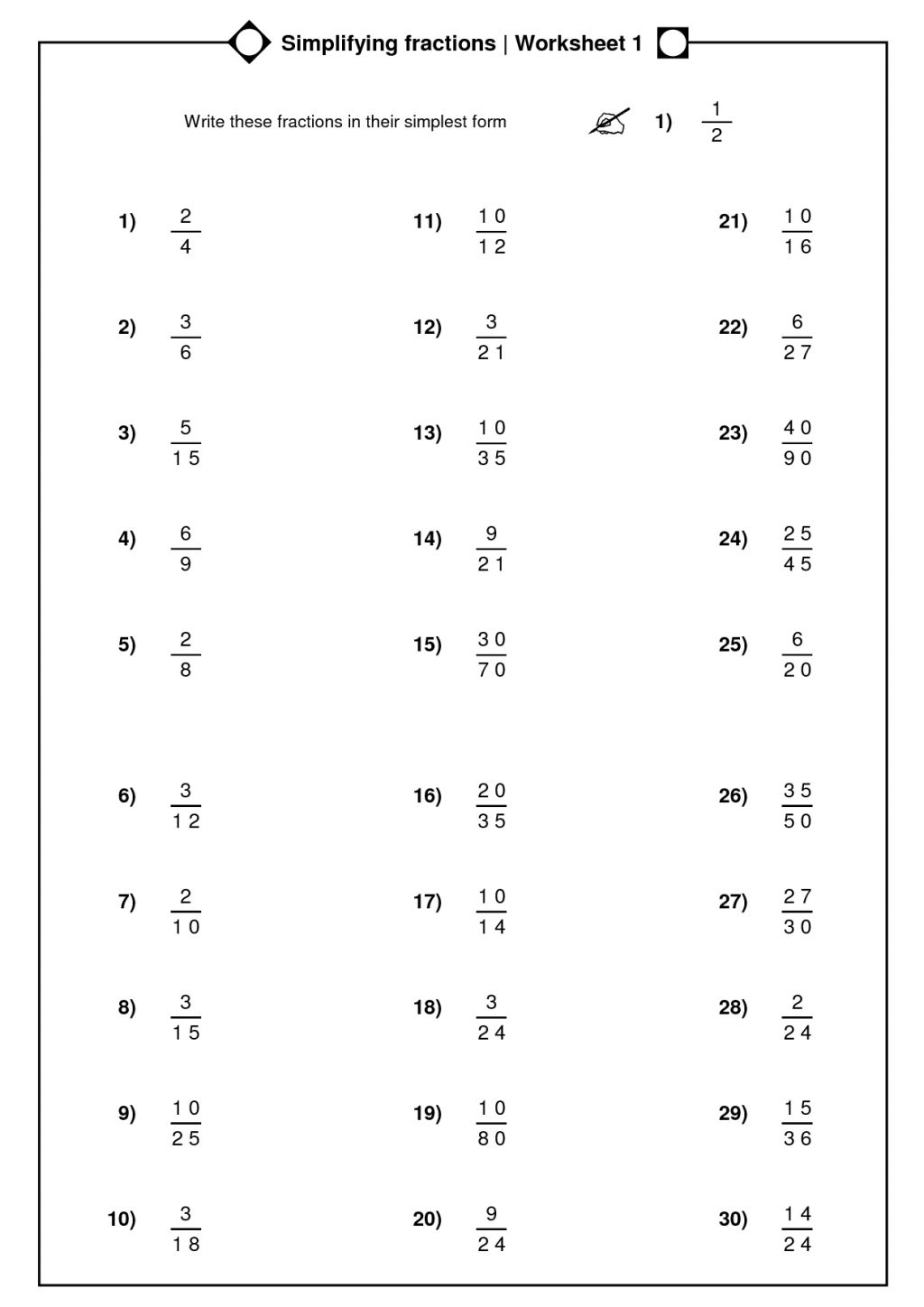
Unlocking Math Success: Properties in Worksheet Explained

Mathematics is often regarded as a daunting subject, full of abstract concepts and complex equations. Yet, at its core, math is incredibly systematic and beautiful, revealing its true elegance when its underlying properties are understood. In this extensive post, we will delve into the intriguing world of mathematical properties, offering insights into how these can be used to unlock a deeper understanding and success in solving math problems, especially as found in worksheets.
Understanding Math Properties

Math properties are fundamental truths that help us understand how numbers and operations interact. They are not merely theoretical; these properties are practical tools used daily in problem-solving. Here, we will explore some pivotal properties:
- Commutative Property: Allows numbers in an addition or multiplication to be swapped without affecting the outcome.
- Associative Property: Permits the regrouping of numbers in addition or multiplication.
- Distributive Property: Connects multiplication over addition or subtraction.
- Identity and Inverse Properties: Introduces the concepts of identity elements (numbers that do not change others) and inverses (numbers that, when added to or multiplied with others, yield the identity).
📚 Note: Understanding these properties not only simplifies calculations but also provides a structured approach to complex problems.
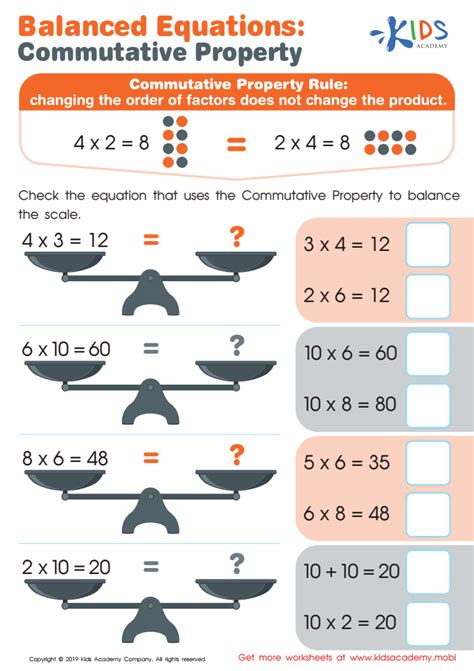
The Commutative Property in Action

The Commutative Property, simply put, says that the order of operations in addition or multiplication doesn’t change the result. This can be represented as:
- For Addition: ( a + b = b + a )
- For Multiplication: ( a \times b = b \times a )
Consider this example:
If you have a problem like 3 + 5 = 8 , it's the same as 5 + 3 = 8 . In worksheets, this property helps students recognize patterns and verify answers by reordering numbers.
The Associative Property

This property tells us that the way numbers are grouped in an addition or multiplication doesn’t affect the result. Here are the mathematical representations:
- For Addition: ( (a + b) + c = a + (b + c) )
- For Multiplication: ( (a \times b) \times c = a \times (b \times c) )
Example:
Given a problem 2 + (3 + 4) = 9 , it's identical to (2 + 3) + 4 = 9 . This property helps in simplifying calculations, particularly when working with numbers that have special properties like zero or one.
The Distributive Property
Perhaps one of the most useful properties for algebraic manipulation, the Distributive Property involves distributing a number to terms inside a parenthesis. The rule is:
( a \times (b + c) = (a \times b) + (a \times c) )
Consider this scenario:
If you have 3 \times (5 + 2) = 3 \times 5 + 3 \times 2 = 15 + 6 = 21 , it simplifies the task by breaking complex problems into smaller, more manageable parts.
Identity and Inverse Properties

The Identity Property indicates that there are numbers, known as identity elements, which when added or multiplied with any number, do not change the number:
- Addition Identity: ( a + 0 = a )
- Multiplication Identity: ( a \times 1 = a )
The Inverse Property introduces the idea of an inverse for each number:
- Additive Inverse: a + (-a) = 0
- Multiplicative Inverse: a \times \frac{1}{a} = 1
These properties simplify equations and make solving for unknowns more straightforward.
| Property | Example |
|---|---|
| Commutative | 2 + 5 = 5 + 2 |
| Associative | (4 + 5) + 1 = 4 + (5 + 1) |
| Distributive | 3 \times (2 + 3) = 3 \times 2 + 3 \times 3 |
| Identity (Additive) | 6 + 0 = 6 |
| Inverse (Additive) | 5 + (-5) = 0 |

To truly appreciate and apply these properties, students must practice:
- Recognizing and using properties in given problems
- Checking answers using alternative methods
- Engaging in group work or discussions to exchange insights on different approaches
💡 Note: Math properties are not just for solving problems; they help build a deeper conceptual understanding of numbers and operations.
In summary, understanding and applying mathematical properties can significantly enhance your success with math worksheets and beyond. From simplifying complex equations to verifying calculations, these properties are not just abstract rules; they are the keys to unlocking the beauty and logic of mathematics. By recognizing patterns, understanding the reasons behind operations, and applying these principles systematically, students can build a strong foundation in math, transforming what might initially seem intimidating into a subject full of wonder and clarity.
What is the difference between the Commutative and Associative Properties?

+
The Commutative Property relates to the order of numbers in an operation, allowing them to be swapped, whereas the Associative Property deals with how numbers are grouped without affecting the result.
Why is the Distributive Property useful?

+
It simplifies expressions by breaking down complex problems into smaller, easier to manage pieces, allowing for algebraic manipulation that can solve complex equations or factor polynomials.
Can these properties help with mental math?

+
Absolutely! Recognizing and using these properties can facilitate mental calculations by allowing for easier grouping, reordering, and simplification of math problems.