Trig Ratios Worksheet Answers: Practice and Mastery
Trigonometric Ratios are fundamental in the world of mathematics, particularly in geometry and the analysis of right triangles. For students and educators alike, mastering trigonometry can open doors to understand more complex mathematical and physical principles. Here, we will delve into a comprehensive guide on trigonometric ratios, offering practice problems, their answers, and tips for mastering this crucial mathematical subject.
Introduction to Trigonometric Ratios
The three primary trigonometric ratios - sine (sin), cosine (cos), and tangent (tan) - are ratios of the sides of right triangles relative to specific angles. Let’s define them:
- Sine of an angle = opposite/hypotenuse
- Cosine of an angle = adjacent/hypotenuse
- Tangent of an angle = opposite/adjacent
The Unit Circle

Understanding the unit circle can enhance your grasp of trigonometric ratios. This circle has a radius of 1, centered at the origin of the coordinate plane. Here, sine and cosine represent the y-coordinate and x-coordinate of a point on the circle:
- Sine = y-coordinate
- Cosine = x-coordinate
When mastering trigonometry, remember that these ratios apply to any angle, not just those within right triangles.
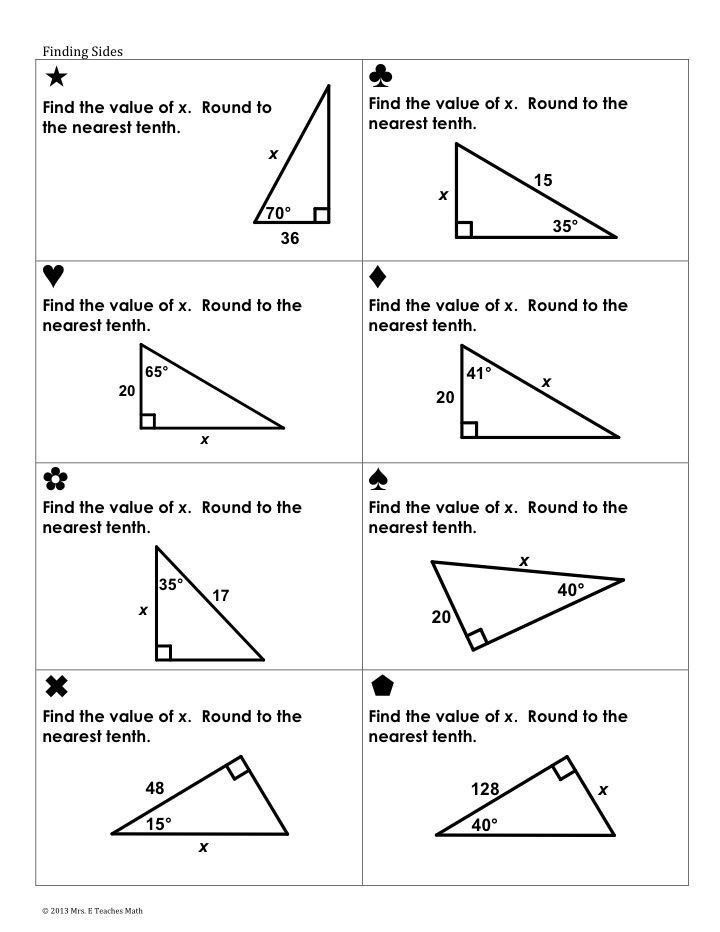
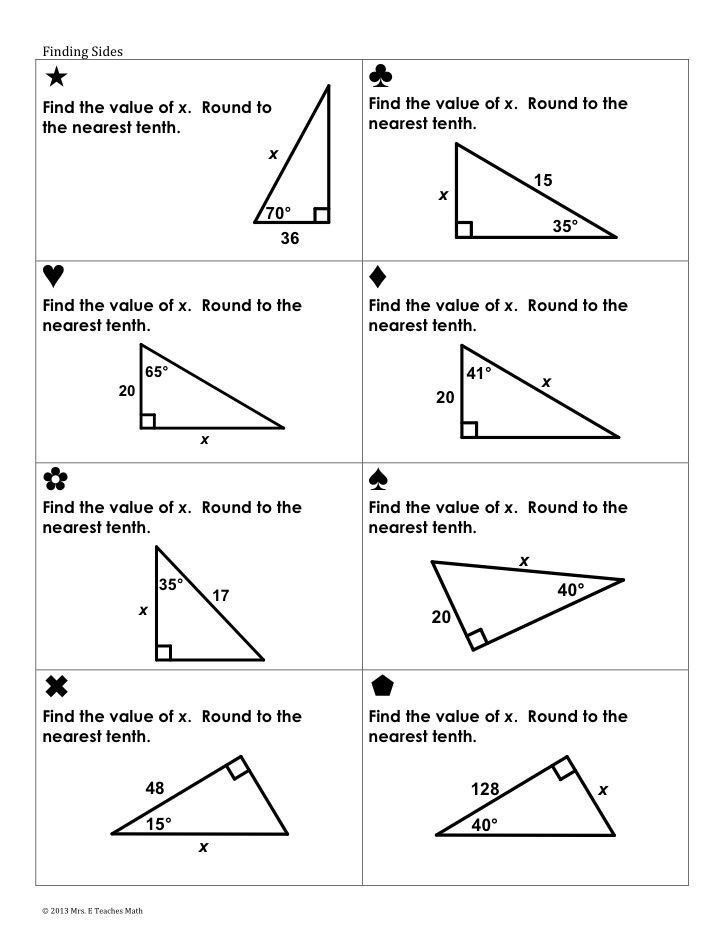
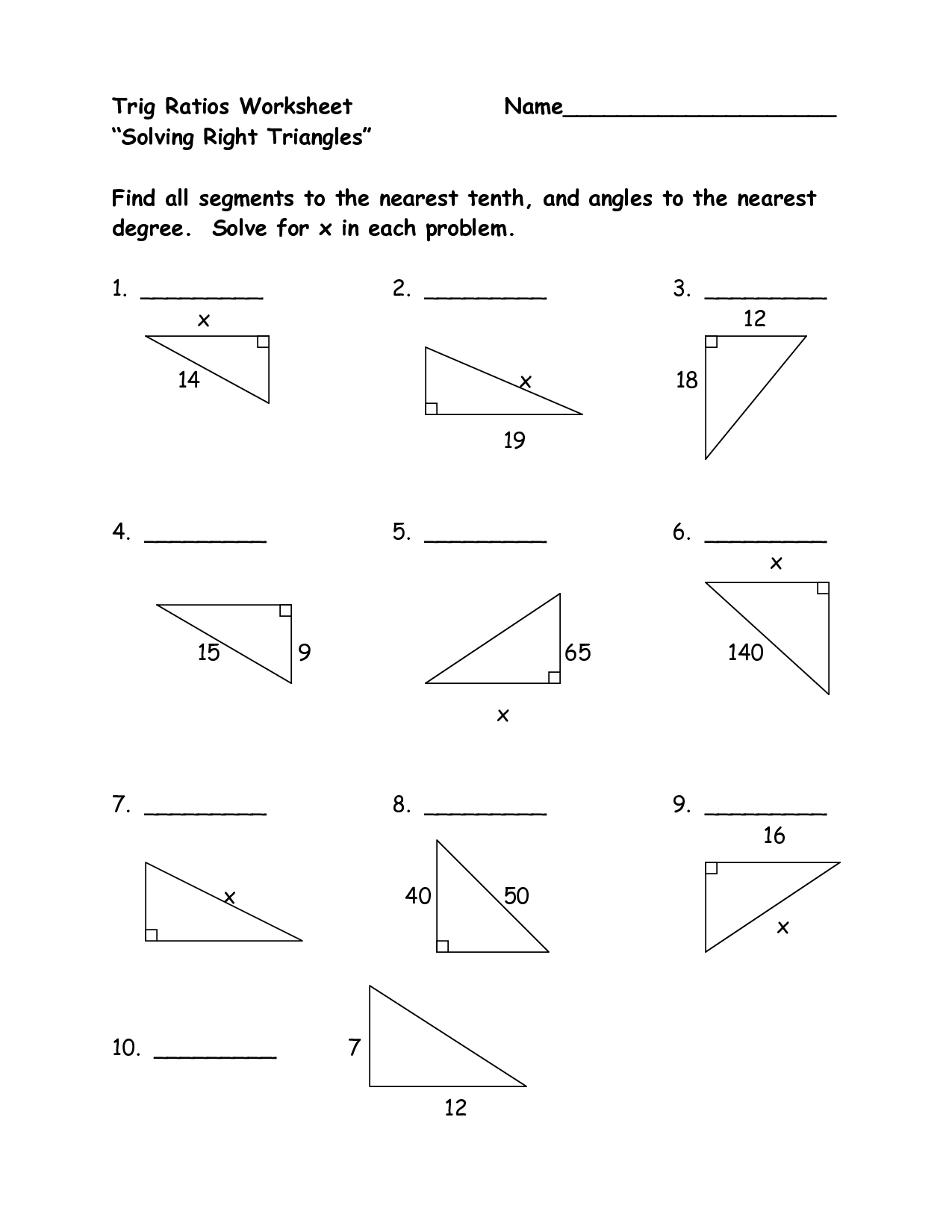
Trigonometric Ratios Worksheet

Let’s dive into a sample worksheet designed to help practice these trigonometric ratios:
Practice Problems
Problem 1: Given a right triangle with sides a = 3, b = 4, and c = 5, calculate sin(θ), cos(θ), and tan(θ) for θ.
| Side | Value |
|---|---|
| a (opposite) | 3 |
| b (adjacent) | 4 |
| c (hypotenuse) | 5 |
🌟 Note: The values provided assume θ is opposite to side a.
Answers:

Sin(θ) = 3⁄5 = 0.6
Cos(θ) = 4⁄5 = 0.8
Tan(θ) = 3⁄4 = 0.75
Steps to Solve Trigonometric Ratios
To solve problems related to trigonometric ratios, follow these steps:
- Identify the right triangle: Determine which angle you’re solving for.
- Label the sides: Opposite, adjacent, and hypotenuse relative to the angle of interest.
- Apply the formula: Use the appropriate trigonometric ratio (sin, cos, or tan) to find the value.
- Calculate: Solve the fraction or ratio to find the trigonometric value.
Using the Unit Circle for More Complex Angles

Beyond 90 degrees, trigonometric ratios can be understood through the unit circle:
- Sine of an angle greater than 90° becomes positive or negative based on the quadrant.
- Cosine reflects the angle’s position on the x-axis.
- Tangent is sin/cos, which might result in undefined values when cos is 0.
Trigonometric Identities and Equations

Trigonometric identities are equations that are true for all angles:
- Pythagorean Identity: sin²(θ) + cos²(θ) = 1
- Complementary Angle Identities: sin(90° - θ) = cos(θ) and cos(90° - θ) = sin(θ)
To practice, solving these equations or proving identities can reinforce your understanding of trigonometric functions:
Example: Prove sin(π - θ) = -sin(θ)
Conclusion
The mastery of trigonometric ratios not only allows you to solve mathematical problems but also enhances your understanding of physics, engineering, and other fields. Remember the importance of:
- The unit circle in understanding angle properties.
- Identities and equations for solving problems.
- Labeling sides correctly in right triangles.
Through consistent practice, you can achieve a high level of proficiency in this essential area of mathematics.
Why are trigonometric ratios important in real life?

+
Trigonometric ratios are used in fields like engineering, physics, architecture, and computer graphics for calculating distances, angles, heights, and other measurements. They help in navigation, construction, and even in understanding wave functions in physics.
How can I remember the trigonometric ratios?

+
Mnemonics are often helpful. For example, SOHCAHTOA where “Sine = Opposite over Hypotenuse,” “Cosine = Adjacent over Hypotenuse,” and “Tangent = Opposite over Adjacent.”
What are the angles where trigonometric ratios are undefined?
+
Tangent (and cotangent) is undefined at 90° or 270° because the adjacent side is zero, making the ratio division by zero, which is undefined in mathematics.