5 Easy Steps to Master Point Slope Formula

Understanding the point-slope form of a line's equation is fundamental for anyone delving into algebra or calculus. This form, expressed as y - y1 = m(x - x1), where m represents the slope and (x1, y1) denotes a point on the line, provides a straightforward method to identify the characteristics of linear equations. In this blog post, we'll walk through the 5 easy steps that can help you master this formula effortlessly.
Step 1: Understand the Basics
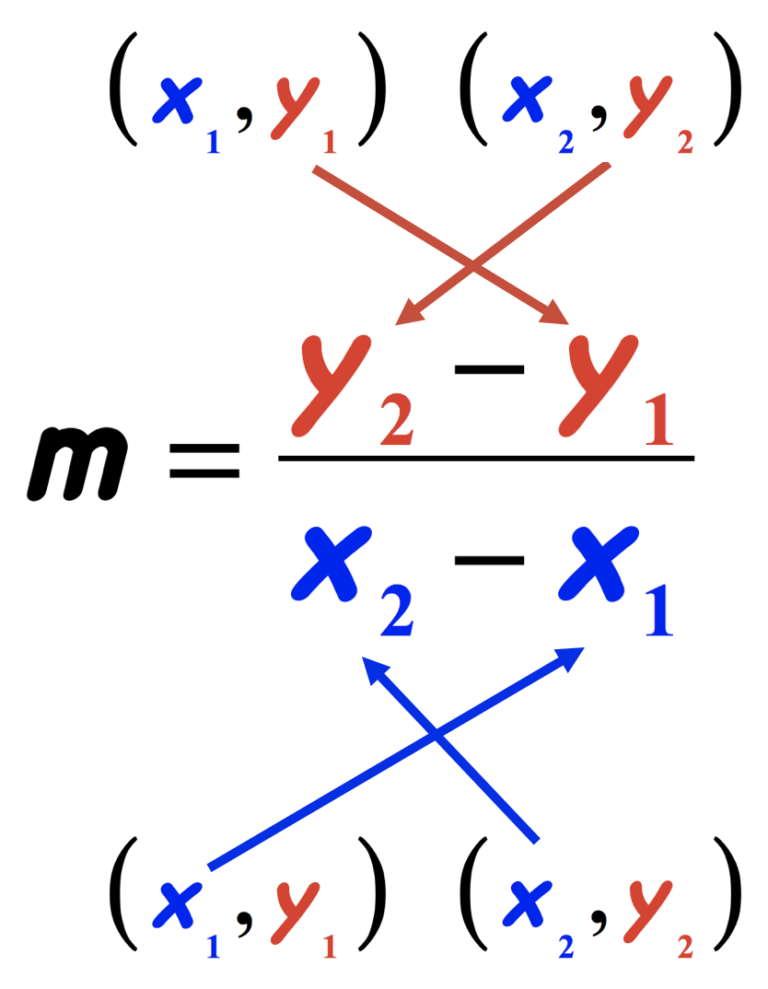
Before diving into how to use the point-slope formula, let’s ensure we have a solid foundation:
- Slope (m): This measures the steepness of the line, calculated as the change in y divided by the change in x.
- Point on the Line: You need one point (x1, y1) through which the line passes.
Understanding these components will make the rest of the process much more straightforward.
Step 2: Plugging in the Values

With the basics covered, here’s how to plug the values into the formula:
- Identify the slope, m.
- Choose a point on the line, (x1, y1).
- Substitute these values into the formula y - y1 = m(x - x1).
📝 Note: Remember, you can use any point on the line, but choose one that simplifies calculations where possible.
Step 3: Solve for y

Now, let’s manipulate the equation to solve for y:
- First, distribute the slope m on the right side of the equation.
- Then, solve for y by isolating it on one side of the equation.
Here’s an example:
| Given | Slope (m) = 2, Point = (1, 3) |
|---|---|
| Plugging In | y - 3 = 2(x - 1) |
| Distribute Slope | y - 3 = 2x - 2 |
| Solve for y | y = 2x - 2 + 3 |
| Final Equation | y = 2x + 1 |

Step 4: Convert to Other Forms

Sometimes, you might need to convert the point-slope form to the slope-intercept form (y = mx + b) or the standard form (Ax + By = C). Here are the conversions:
- To Slope-Intercept Form: Isolate y as shown in the example above.
- To Standard Form: Arrange the equation so that x and y are on the left side and any constants are on the right.
Understanding these conversions will enhance your flexibility with linear equations.
Step 5: Practice, Practice, Practice

Mastery comes with practice:
- Work through several examples to solidify your understanding.
- Try graphing lines from point-slope form to visualize the connection.
The more you practice, the more intuitive this formula will become.
Now that we've gone through these steps, let's wrap up by reinforcing that the point-slope formula is a versatile tool for understanding linear equations. Whether you're solving for a line's equation, converting forms, or working with real-world data, these steps provide a clear path to mastering this essential algebra tool.
Why is point-slope form useful?

+
Point-slope form is incredibly useful because it lets you find the equation of a line with only two pieces of information: one point and the slope. This form is particularly handy when dealing with straight lines in various mathematical problems.
What’s the difference between point-slope form and slope-intercept form?

+
The main difference is in what they emphasize. Point-slope form focuses on a point and the slope, whereas slope-intercept form (y = mx + b) emphasizes the slope (m) and y-intercept (b). Point-slope form can easily be converted to slope-intercept form by solving for y.
Can you use point-slope form with vertical or horizontal lines?

+
Yes, but with some limitations. For horizontal lines, the slope is zero, and for vertical lines, the slope is undefined. Horizontal lines would have an equation like y = y1 while vertical lines would be x = x1. Point-slope form isn’t as useful in these cases, but it’s still applicable when you’re dealing with lines with defined slopes.