5 Ways to Master Rational Numbers Number Line Plotting
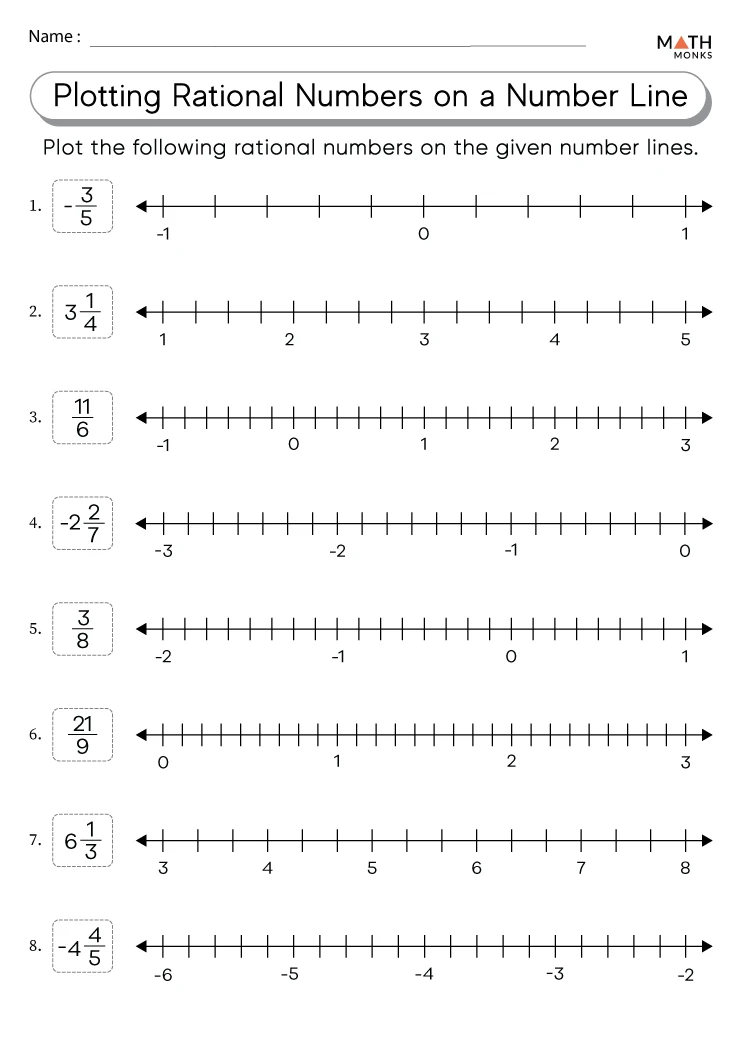
In mathematics, plotting rational numbers on a number line can seem like a daunting task, but with the right strategies and understanding, it becomes a manageable and even fascinating skill. This skill is not only fundamental in mathematical learning but also essential for higher studies and practical applications in various fields. Here are five effective ways to master plotting rational numbers on the number line:
1. Understand the Basics of Rational Numbers

What are Rational Numbers?
- A rational number can be expressed as a fraction \frac{a}{b} , where a and b are integers and b is not zero.
- These numbers include integers, fractions, and terminating or repeating decimals.

When plotting rational numbers on a number line, the key is to recognize their place in relation to integers. Here’s how:
2. Scaling the Number Line

Scaling Matters
Decide on an appropriate scale for your number line:
- If the numbers you are plotting are very close, you might need to zoom in significantly, making each unit represent a small fraction.
- For larger ranges, a bigger unit scale might be necessary.
| Scenario | Example | Recommended Scale |
|---|---|---|
| Close numbers (between 0 and 1) | Plotting \frac{1}{4}, \frac{1}{2}, \frac{3}{4} | Each unit = \frac{1}{8} |
| Spread out numbers | Plotting -2 \frac{1}{2}, 0, 3 \frac{1}{3} | Each unit = 1 |

⚠️ Note: The scale you choose directly affects the readability and accuracy of your plotting.
3. Using Decimal Form

Converting Rational Numbers to Decimal
Converting rational numbers into their decimal form can simplify the process of plotting, especially for repetitive fractions or when dealing with mixed numbers:
- Convert \frac{2}{3} to 0.6667
- Plot 0.6667 between 0 and 1, slightly closer to 1
When dealing with repeating decimals or long division, this step helps in locating the exact point on the number line.
4. Making Use of Number Line Divisions

Divide and Conquer
Divide the number line segments into equal parts based on the denominators of your rational numbers:
- If plotting \frac{1}{4} , divide each unit into four parts.
- If your numbers are within a specific range, consider dividing only that segment of the line.
This method allows for a more intuitive placement of rational numbers relative to known integers and other points.
5. Practice and Visualization
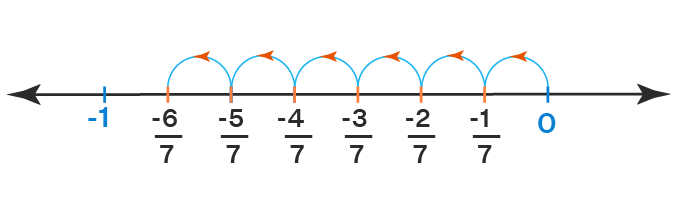
Engage with the Number Line
Visualizing and physically plotting these numbers can be an excellent practice:
- Create number lines on paper or use digital tools to plot points.
- Compare where these points fall in relation to each other and to known integers.
Regular practice enhances your understanding of spacing between numbers and builds your confidence in plotting:
🔎 Note: Visualization not only aids in mastering number line plotting but also deepens your overall grasp of numerical values.
To truly master plotting rational numbers on a number line, remember to:
- Understand the nature of rational numbers.
- Use an appropriate scale to maximize accuracy.
- Convert to decimal form when necessary for precision.
- Divide the number line based on denominators for placement.
- Engage in regular practice to internalize the relationships between numbers.
Why are rational numbers important in mathematics?

+
Rational numbers are crucial because they provide a foundation for understanding arithmetic operations, proportions, and measurements, which are applicable in various scientific and everyday scenarios.
How do you decide the scale of the number line?

+
The scale depends on the range of numbers to be plotted. Use smaller units for numbers close together and larger units for numbers spread apart to ensure readability and precision.
Can I plot irrational numbers on the same number line as rational numbers?
+
Yes, but for irrational numbers like π or √2, you would need to approximate their positions using decimal equivalents, which might not be exact due to the irrational nature of these numbers.
What are the common mistakes in plotting rational numbers?
+
Common errors include incorrect scaling, misplacement due to poor understanding of decimal expansion, and confusion between positive and negative fractions.