5 Essential Point Slope Form Worksheets for Mastery

Understanding Point-Slope Form is a critical part of algebra education, enabling students to solve linear equations with precision. This form of the equation provides an efficient way to graph lines and understand their slopes with a clear and straightforward method. By employing point-slope form worksheets, educators and students can master the necessary skills, making algebra accessible and exciting.
Why Use Point-Slope Form Worksheets?

Point-slope form worksheets are designed to reinforce the key mathematical concepts of linear functions, slope, and intercepts through:
- Practical Application: Real-life scenarios and algebraic operations are practiced, boosting students' problem-solving abilities.
- Visual Learning: Graphing lines from point-slope equations helps in visualizing the relationship between slopes and intercepts.
- Versatility: Suitable for various learning levels, from beginners to those seeking mastery.
- Comprehensive Coverage: These worksheets cover not just the concept of point-slope form but also the conversion to and from other equation forms.
5 Essential Point-Slope Form Worksheets for Mastery

1. Introduction to Point-Slope Form
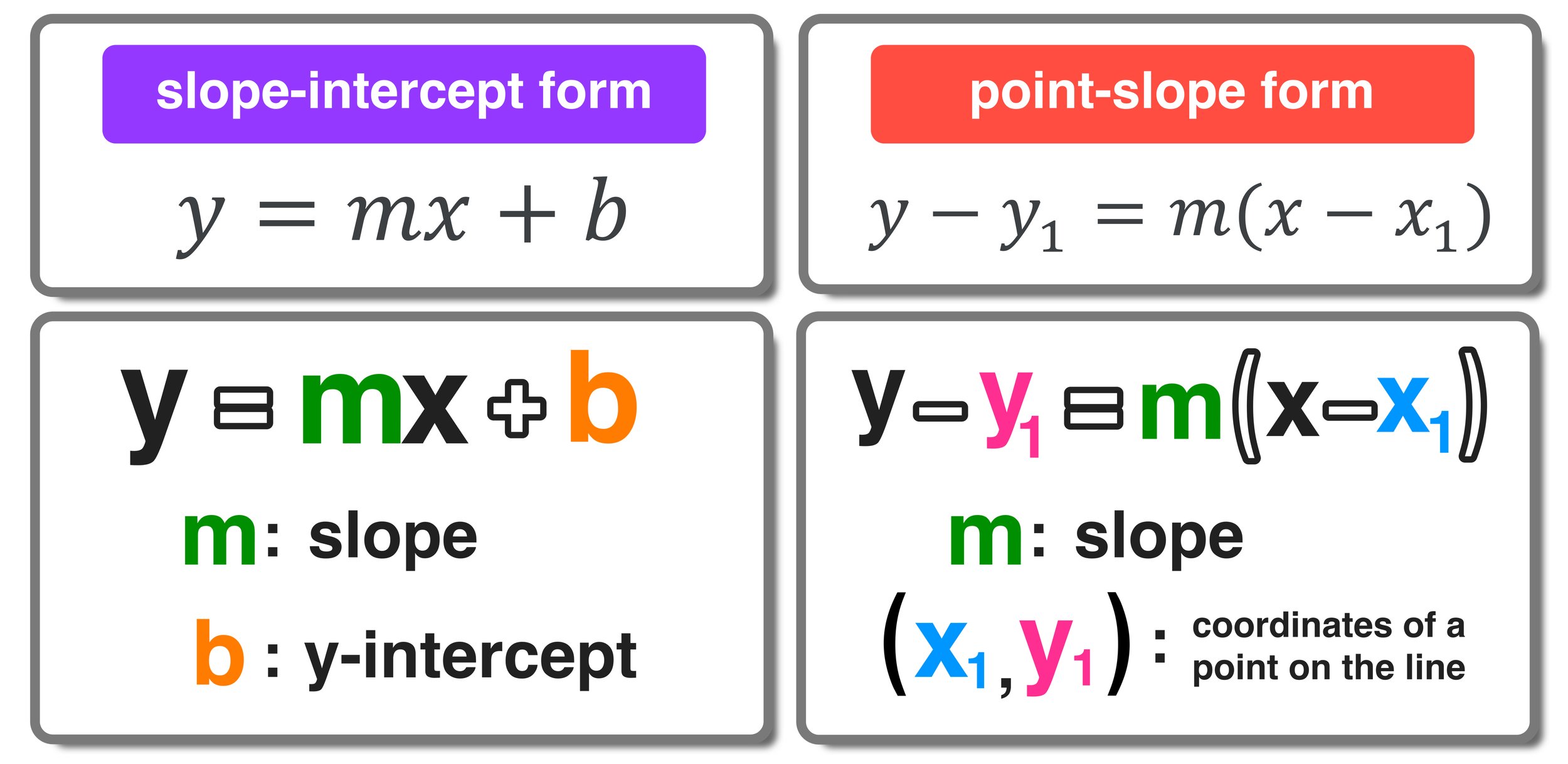

This worksheet is designed for beginners, focusing on:
- Defining point-slope form:
y - y1 = m(x - x1), where m is the slope and (x1, y1) are coordinates of a point on the line. - Identifying the components of the equation.
- Practicing graphing lines using given points and slopes.
- Converting from point-slope to slope-intercept form, y = mx + b.
2. Graphing Lines in Point-Slope Form

Students are encouraged to:
- Graph lines using the given point and slope.
- Determine intercepts and additional points to enhance their understanding of the line.
- Compare lines with different slopes and intercepts, reinforcing the differences and similarities.
- Analyze the effect of changing the point or slope on the graph.
3. Writing Equations in Point-Slope Form

This worksheet shifts the focus to:
- Writing equations given two points.
- Calculating the slope using the slope formula: (y2 - y1) / (x2 - x1).
- Constructing equations from a table of values or coordinate pairs.
- Transitioning between point-slope, slope-intercept, and standard form.
4. Advanced Point-Slope Problems


The worksheet pushes students to apply:
- Solving for parallel or perpendicular lines using point-slope form.
- Finding the equation of a tangent line to a curve at a given point.
- Incorporating real-world applications, like physics problems involving velocity and displacement.
- Understanding the impact of the point-slope form on calculation accuracy and conceptual understanding.
5. Conversion and Application

The focus here is on transitioning:
- Converting equations from one form to another, specifically from point-slope to standard form: Ax + By = C.
- Exploring the uses of the equation in real-life problem-solving scenarios.
- Applying the principles of point-slope form to geometric concepts like vectors and parametric equations.
💡 Note: Mastering these worksheets requires consistent practice and conceptual understanding, not just memorization. Encourage students to think logically about the relationships between the given components of the equation and the resulting line.
Mastering point-slope form through these carefully designed worksheets not only equips students with the algebra tools needed for success, but also fosters a deeper appreciation for the beauty of linear equations. Whether graphing lines, solving complex problems, or applying these skills in real-world scenarios, the journey to mastery is made clear and rewarding with the right approach and resources.
What is point-slope form used for?

+
Point-slope form is used for creating linear equations based on a single point on the line and its slope. It’s ideal for graphing lines, solving for parallel or perpendicular lines, and understanding the geometric representation of lines.
Can I convert any equation of a line to point-slope form?

+
Yes, any equation of a line can be converted to point-slope form, given you have at least one point on the line and the line’s slope. This can be helpful for understanding the equation’s components and plotting the line.
How do I practice with point-slope form effectively?

+
Effective practice involves working through a variety of problems, from basic to complex, including graphing, solving for equations, and applying the form in real-world scenarios. Repetition and understanding concepts rather than just solving for answers are key.



