Projectile Motion Problems: Simple Worksheet Solutions

Projectile motion is a common topic in introductory physics courses, often presented through worksheets to help students understand the principles of motion under the influence of gravity. This comprehensive guide will explore various projectile motion problems, explain the concepts involved, and provide straightforward solutions for a typical worksheet. Let's dive into understanding how projectiles behave under the influence of gravity.
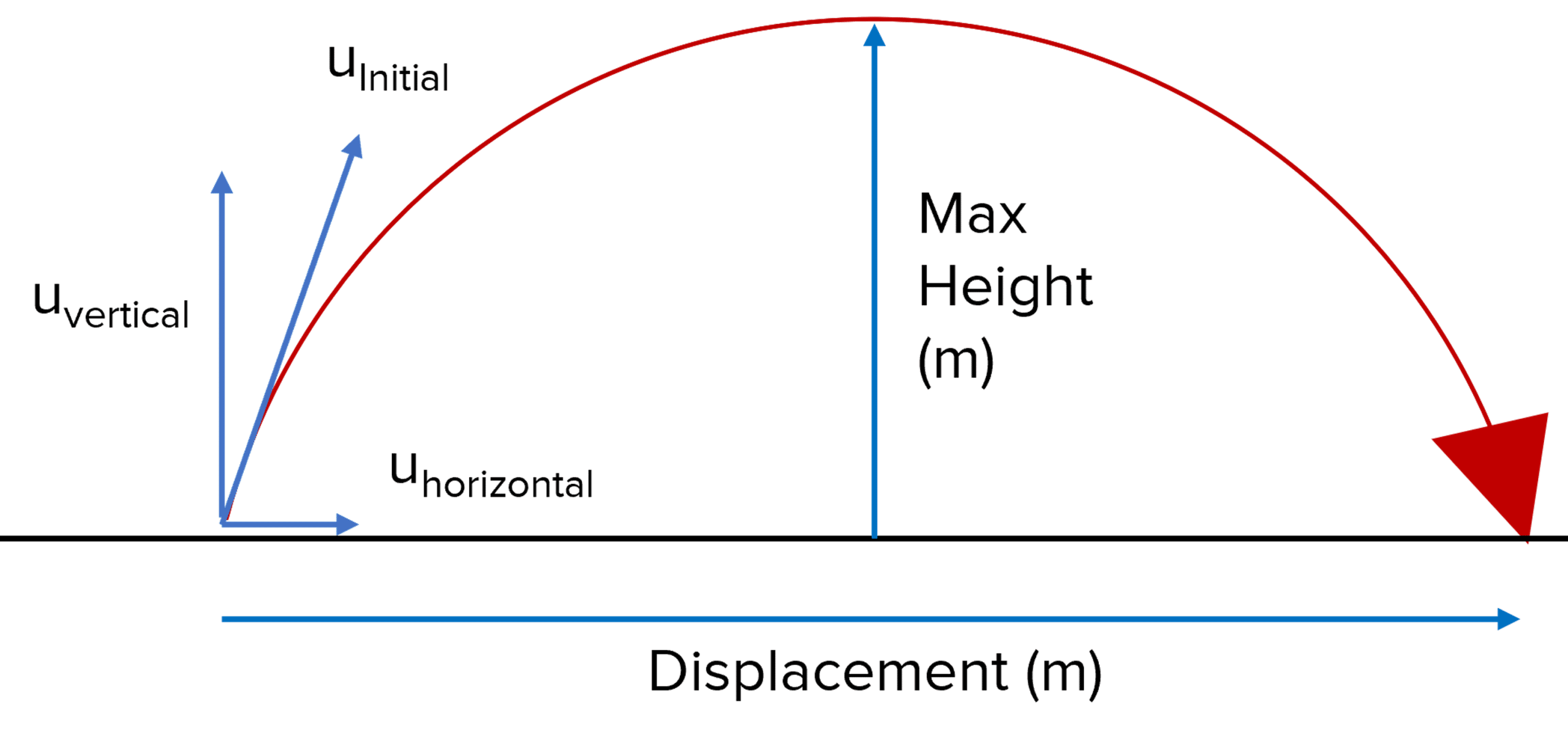
Understanding Projectile Motion

Projectile motion refers to the movement of an object or body through the air, subject only to the acceleration of gravity. Key concepts include:
- Horizontal Motion: This component is uniform, meaning the horizontal velocity remains constant if there's no air resistance.
- Vertical Motion: This is influenced by gravity, where the acceleration due to gravity is approximately 9.8 m/s² downward.
- Time of Flight: The duration the projectile is in the air.
- Range: The total horizontal distance traveled by the projectile.
- Maximum Height: The peak altitude reached by the projectile.
⚠️ Note: For simplicity, this post assumes no air resistance unless specified.
Example Problems
Problem 1: Time of Flight

A ball is thrown horizontally from a height of 50 meters with an initial horizontal velocity of 10 m/s. Determine how long it will take to hit the ground.
Solution:
We use the vertical motion equation:
h = 0.5 * g * t² + v0y * t
Where:
- h = initial height (50 meters)
- g = acceleration due to gravity (-9.8 m/s²)
- v0y = initial vertical velocity (0 m/s, because thrown horizontally)
Solving for t:
50 = 0.5 * 9.8 * t²
50 = 4.9 * t²
t² = 50 / 4.9
t = √(10.2) ≈ 3.19 seconds
Problem 2: Range of Projectile

A football is kicked at an angle of 45 degrees with an initial speed of 15 m/s. What is the range?
Solution:
The range of a projectile at an angle θ can be calculated using:
R = (v0² * sin(2θ)) / g
Here, v0 = 15 m/s, θ = 45°, and g = 9.8 m/s²:
R = (15² * sin(90°)) / 9.8 ≈ 23.4 meters
⚠️ Note: The range equation assumes an ideal situation where the initial and final heights are the same.
Problem 3: Maximum Height

A rocket is launched straight up with an initial velocity of 50 m/s. Calculate the maximum height it reaches.
Solution:
At the highest point, the vertical velocity becomes zero:
v_y² = v0² - 2gh
0² = 50² - 2 * 9.8 * h
h = (50²) / (2 * 9.8) ≈ 127.55 meters
Problem 4: Projectile Path

An archer shoots an arrow at an angle of 60 degrees from the horizontal with a speed of 20 m/s. Describe the path of the arrow.
Solution:
The path of the projectile follows a parabolic trajectory:
- Horizontal component (v0x): 20 * cos(60°) = 10 m/s
- Vertical component (v0y): 20 * sin(60°) ≈ 17.3 m/s
- Using the equation of motion:
x = v0x * t
y = v0y * t - 0.5 * g * t²
The combination of these equations results in a parabolic shape due to the constant horizontal motion and the acceleration due to gravity in the vertical direction.
Solving Complex Scenarios

Sometimes, the initial conditions or environments might complicate the calculations:
- Wind Resistance: Include a drag force in calculations for more realistic scenarios.
- Variable Terrain: If the projectile lands on an incline, use projectile motion equations to find the landing point and then adjust for the terrain’s geometry.
- Projectiles Fired at Non-zero Angle with Earth: Apply corrections for the curvature of the Earth for long-range projectiles.
In summary, this guide has walked you through the fundamental principles of projectile motion, provided solutions to common worksheet problems, and highlighted how to approach more complex scenarios. Understanding projectile motion not only helps in physics but also has practical applications in sports, military ballistics, and aerospace engineering.
What factors influence the time of flight of a projectile?
+
The primary factors are the initial vertical velocity and the height from which the projectile is launched. The higher the initial height or the greater the upward component of initial velocity, the longer the projectile will stay in the air.
Can you calculate the range if the launch height is different from the landing height?

+
Yes, you would need to adjust the range equation to account for the height difference. The formula becomes more complex, incorporating both initial and final heights into the calculation.
How does air resistance affect a projectile’s path?

+
Air resistance reduces both the range and the maximum height of a projectile. It shortens the flight time and alters the trajectory from a parabola to a more complex curve.



