5 Tips for Solving One and Two Step Inequalities

Mastering inequalities is a cornerstone of algebra that unlocks the door to more advanced mathematical problems. For students and math enthusiasts alike, understanding how to navigate through one and two-step inequalities is essential. Whether you're preparing for an exam, tackling homework, or just seeking to broaden your mathematical horizon, here are five effective tips to help you solve inequalities with confidence and precision.
1. Understand the Basics of Inequalities


Before diving into the complexities of solving inequalities, ensure you have a firm grasp on the basic concepts:
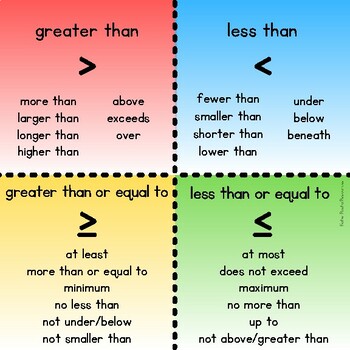
- Symbols: Recognize the difference between
<,>,≤, and≥. - Solution Set: Unlike equations, inequalities have a range of values rather than one exact solution.
- Direction of Inequality: Remember that inequalities maintain their direction unless you multiply or divide by a negative number, which reverses the inequality sign.
2. Transform Inequalities into Equations
One effective strategy to solve inequalities, particularly those with one or two steps, is to treat them like equations:
- Isolate the Variable: Just as with equations, your goal is to get the variable alone on one side of the inequality. For instance, if you have
3x + 5 > 14, you would subtract 5 from both sides and then divide by 3. - Handling Negatives: If you multiply or divide by a negative number, remember to reverse the inequality sign. For example, in
-x + 3 < 9, subtracting 3 from both sides gives-x < 6, and dividing by -1 (which reverses the inequality) results inx > -6.
3. Use Properties of Inequalities Wisely

Inequalities share many properties with equations, but with one crucial difference:
- Addition and Subtraction: Adding or subtracting the same number to both sides of an inequality maintains its truth.
- Multiplication and Division: Multiplying or dividing by a positive number keeps the inequality’s direction unchanged. Multiplying or dividing by a negative number flips the direction.
- Properties of Equality: The transitive property (if A > B and B > C, then A > C) also holds for inequalities.
4. Solve Two-Step Inequalities Systematically

Two-step inequalities are not much different from two-step equations. Here’s a step-by-step guide:
- Move the Constant: If the constant is on the same side as the variable, move it to the other side by subtracting or adding it from both sides.
- Divide or Multiply: After isolating the term with the variable, divide or multiply both sides by the coefficient of the variable. Remember to flip the sign if you’re dealing with negatives.
- Check Direction: Double-check that your inequality sign reflects any changes made, especially after operations with negative numbers.
⚠️ Note: When checking your solution, ensure you test at least one value from within the solution range to confirm the inequality holds true.
5. Graph Your Solution

Once you’ve solved your inequality, it’s beneficial to visualize the solution:
- Number Line: Plot the solution on a number line, using an open circle for < or > and a closed circle for ≤ or ≥. Draw arrows to indicate the direction of the inequality.
- Interval Notation: If you prefer, you can express the solution using interval notation, which provides a compact way to describe the solution set.
Embracing these tips not only simplifies the process of solving one and two-step inequalities but also enhances your overall mathematical proficiency. It’s through understanding these foundational skills that one can progress to more complex inequalities and equation systems. Remember, consistent practice is key to mastering inequalities, and with these strategies in hand, you'll find that tackling these problems becomes second nature.
Why do we reverse the inequality sign when multiplying or dividing by a negative number?
+
Multiplying or dividing both sides of an inequality by a negative number flips the relationship between the numbers, essentially inverting the direction of the inequality.
Can inequalities have more than one solution?
+
Yes, inequalities often have a range of values as solutions, rather than a single answer like with equations.
What if the variable disappears when solving an inequality?
+
If the variable disappears, the inequality might not have any solution or might be true for all numbers (e.g., 2 < x when solved gives a contradiction or an identity).



