5 Tricks for Multiplying and Dividing Fraction Negatives

Fractions are a fundamental part of mathematics, and understanding how to manipulate them, especially when they involve negative numbers, can initially seem daunting. However, with a few simple tricks, you can streamline your calculations and become adept at multiplying and dividing these numbers. Let's dive into 5 tricks for multiplying and dividing fraction negatives.
Trick 1: Understand the Rule of Signs

Before tackling multiplication and division, it’s crucial to understand how negative signs affect arithmetic operations:
- The product (or quotient) of two negative numbers is positive.
- The product (or quotient) of a positive number and a negative number is negative.
Here's how you apply this rule:
- Multiply two fractions with the same sign (both positive or both negative), the result is positive.
- Multiply a positive fraction by a negative fraction, the result is negative.
- For division, the same rules apply; think of division as multiplying by the reciprocal of the second fraction.
Trick 2: Reciprocal Conversion for Division
Dividing by a fraction is essentially multiplying by its reciprocal:
- To find the reciprocal, simply invert the fraction (flip the numerator and the denominator).
- For a negative fraction, the sign stays with the number:
| Division | Reciprocal |
| 4 ÷ (-1/3) | = 4 * (-3/1) |

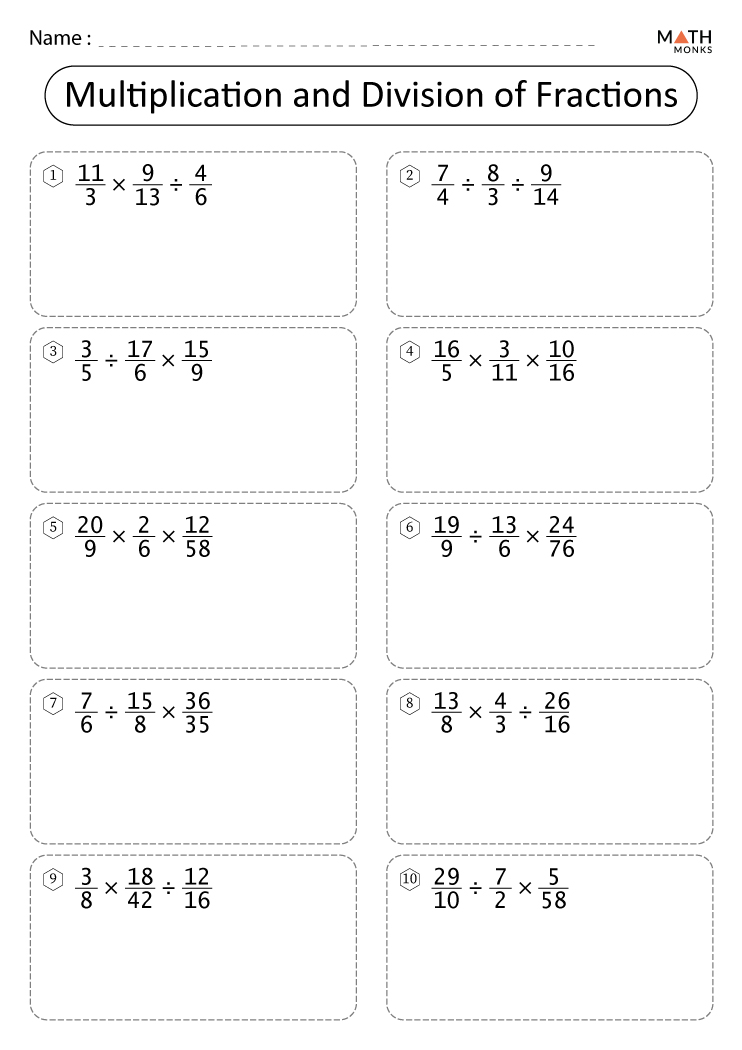
Trick 3: Simplify First, Then Multiply or Divide

Before performing any operations:
- Reduce your fractions to their simplest form.
- This not only simplifies the multiplication or division but also helps in avoiding complex calculations.
Example:
- Simplify 4/8 to 1/2 before multiplying.
- When multiplying (1/2) * (-1/3), you get -1/6 directly.
Trick 4: Use Cross Multiplication for Simplification

Cross multiplication can be a quick way to simplify division, especially when you're working with fractions involving negatives:
- When you divide fractions, multiply the numerator of the first fraction by the denominator of the second, and vice versa.
- This trick works because it reflects the multiplication by the reciprocal in a more visual format:
- (-3/4) ÷ (2/5) = (-3) * 5 / 4 * 2 = -15/8
Trick 5: Keep Track of Signs During Conversions
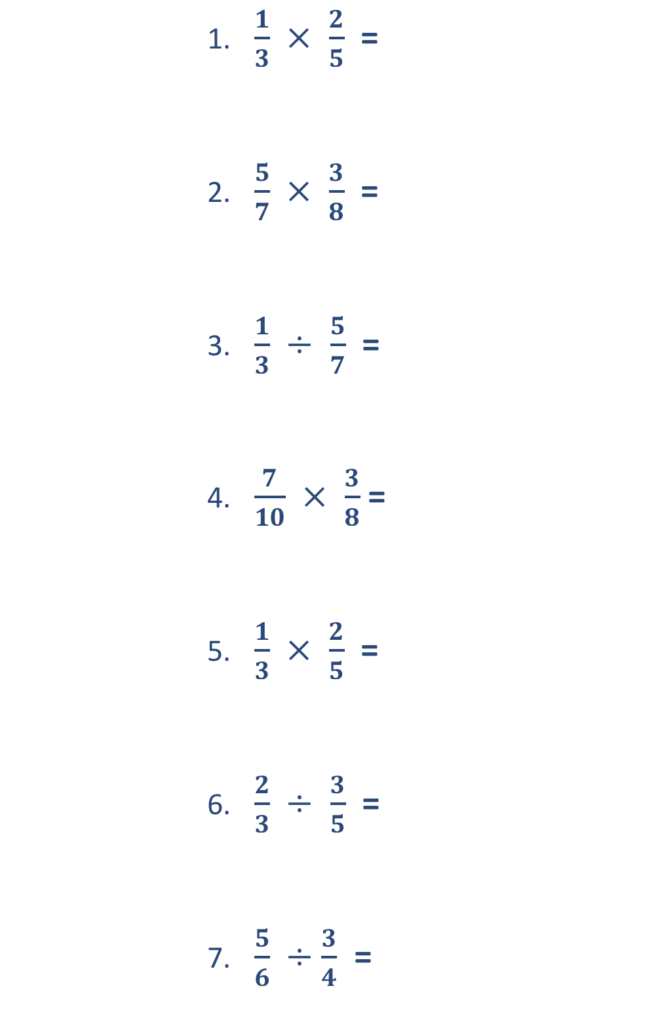
When converting mixed numbers to improper fractions or simplifying complex fractions, it's easy to lose track of the signs:
- Convert the mixed number to an improper fraction.
- Remember to keep the negative sign with the number if it's negative.
Here’s how:
- -1 and 3/4 becomes -7/4
As we've explored these techniques, remember that patience and practice are your allies when working with fractions and negative numbers. These 5 tricks for multiplying and dividing fraction negatives are just the beginning. Regularly applying these methods will ensure that these operations become second nature, making your mathematical endeavors smoother and more efficient.
🎯 Note: Always double-check your signs when dealing with negative fractions to avoid sign errors.
In summary, by understanding the basic rules, converting to reciprocals for division, simplifying before operations, employing cross multiplication for quick checks, and being meticulous with signs, you can navigate through fraction operations with negatives with greater ease and accuracy.
Why is it important to understand the rule of signs in fractions?

+
Understanding the rule of signs is essential as it dictates the sign of the result when multiplying or dividing fractions. This ensures that the operations are performed correctly, especially when dealing with negative fractions.
Can I simplify fractions after multiplying or dividing?

+
Yes, simplification can be done after performing multiplication or division. However, simplifying before operations can reduce complexity and potential for errors.
How do I handle complex fractions with negative numbers?

+
First, simplify the complex fraction if possible, then follow the rules for signs and reciprocals. Always pay attention to how the negative signs interact within and between fractions.