Fun Worksheet: Multiply Decimals by Whole Numbers

In today's educational journey, let's delve into the fascinating world of mathematics by exploring how to multiply decimals by whole numbers. This skill is not just crucial for mathematical understanding but also has practical applications in everyday life, from scaling recipes to financial calculations. Whether you're helping a student with homework, refreshing your own skills, or curious about the process, this comprehensive guide will provide the knowledge you need to multiply decimals with confidence and accuracy.
Understanding the Concept

Multiplying decimals by whole numbers might seem complex at first, but the truth is, it’s built on the principles of whole number multiplication, with a key step at the end. Let’s break it down:
- Ignore the decimal point during the initial multiplication.
- Count the total number of decimal places in the initial numbers.
- Place the decimal point in the product according to the counted places.
Step-by-Step Multiplication Process
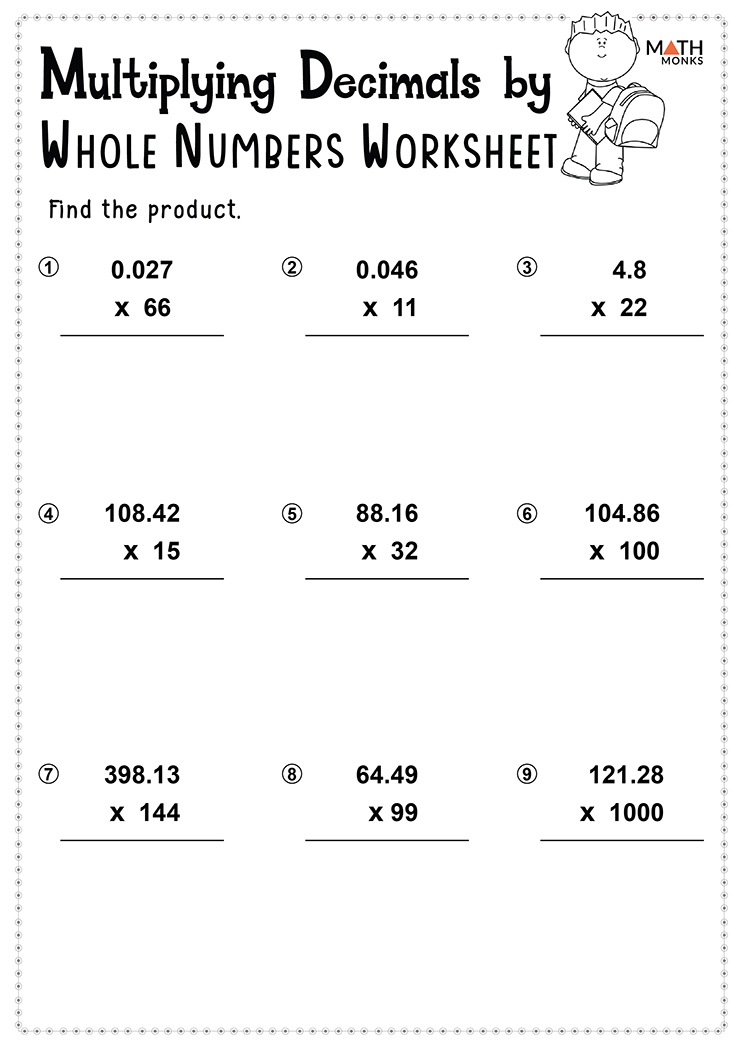
Here’s a structured approach to multiply a decimal by a whole number:
- Set Up the Problem: Write the numbers in alignment, as you would for regular multiplication.
- Ignore the Decimal: For the calculation part, consider the decimal as a whole number.
- Perform Multiplication: Multiply the numbers as if they were whole numbers.
- Count Decimal Places: Count the number of digits to the right of the decimal point in both numbers.
- Place the Decimal: In the product, place the decimal point the same number of places from the right as the total count from step 4.
- Round If Necessary: Depending on the context, round the final result.
Examples to Illustrate

Let’s walk through some examples for clearer understanding:
| Problem | Calculation | Answer |
|---|---|---|
| 2.5 × 4 | (25 × 4) = 100; Move the decimal point 1 place to the left. | 10.0 |
| 3.14 × 5 | (314 × 5) = 1570; Move the decimal point 2 places to the left. | 15.70 |
| 0.23 × 10 | (23 × 10) = 230; Move the decimal point 2 places to the left. | 2.30 |

📘 Note: Remember, multiplying by 10 moves the decimal one place to the right, but we're keeping track of the original position to place the decimal point correctly.
Practical Applications

This skill isn’t just for academic scenarios; here’s how it applies in real life:
- Finance: Calculating taxes, tips, or discounts often involves multiplying by decimal values representing percentages.
- Cooking: Adjusting recipe quantities based on the number of servings requires multiplication by whole numbers.
- Measurement: Multiplying dimensions or quantities when working with blueprints, scaling models, or converting units.
💡 Note: Real-life calculations might require rounding for practicality.
In the end, multiplying decimals by whole numbers is not only foundational for mathematical fluency but also has numerous practical uses. It's about understanding the basics of multiplication and remembering the critical step of placing the decimal point. With practice, this becomes second nature, allowing you to perform calculations swiftly and accurately in both academic and everyday scenarios.
What if I multiply by a larger number?

+
The process remains the same; count the total decimal places and place the decimal point accordingly. However, you might need more room for calculation due to the product’s potential size.
Can I multiply decimals by decimals using the same method?
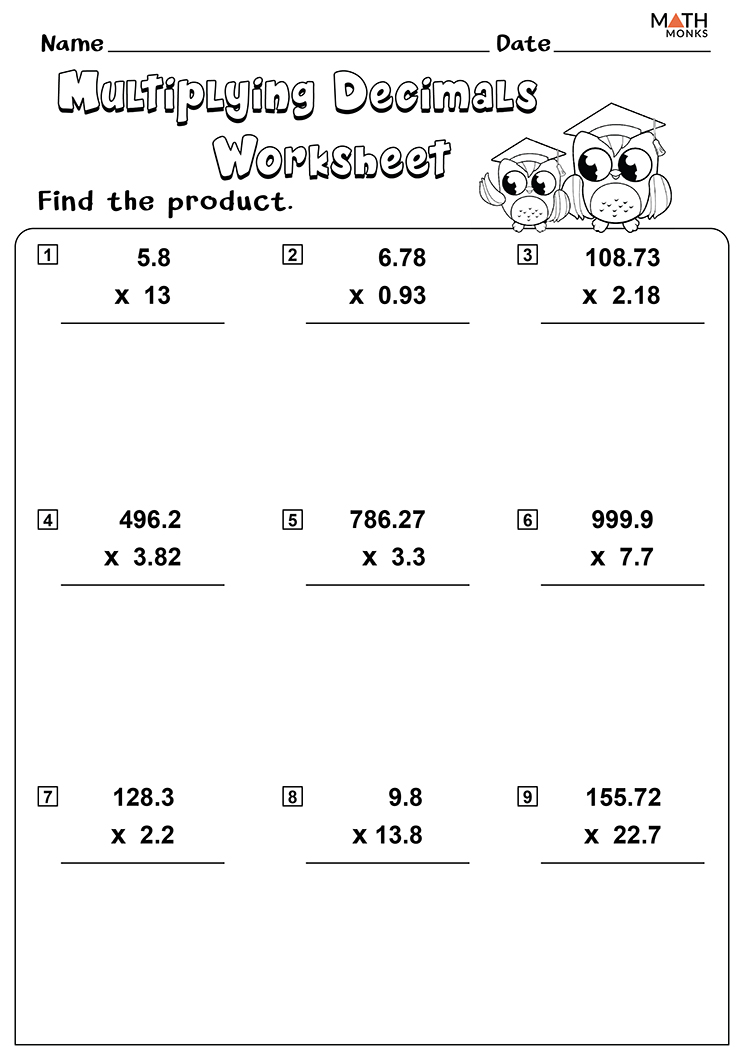
+
Yes, the concept applies. You still count the total decimal places and place the decimal in the product appropriately, considering both numbers now.
Why do I have to count decimal places?

+
Counting decimal places ensures that the product reflects the true value by maintaining the precision of the original numbers.
Does multiplication with decimals always yield a decimal product?

+
No, sometimes, you’ll encounter situations where the result is a whole number, especially if you round off the decimals or if the product naturally results in no decimal.
What about negative numbers?

+
Negative numbers follow the same rules of multiplication; multiply as with positive numbers and then determine the sign by following the rules of multiplication with signs (two negatives make a positive, one of each makes a negative).



