Metric Conversion Worksheet Answers: Simplify Your Learning
In the realm of international business, science, and technology, having a firm grasp of metric conversions is essential. Not only does this skill streamline communication and prevent costly mistakes, but it also helps in understanding various measurements used globally. Whether you are a student, a professional, or simply someone who wants to broaden their knowledge, working through metric conversion worksheets can significantly enhance your understanding. This blog post provides answers to common metric conversion problems, helping you to simplify your learning journey.
Understanding the Metric System

Before diving into conversions, it’s beneficial to understand the basics of the metric system:
- Base Units: The metric system is built on base units like meters for length, grams for mass, liters for volume, etc.
- Prefixes: These denote multiples or submultiples of base units, such as kilo (1000), hecto (100), deca (10), deci (0.1), centi (0.01), milli (0.001).
- Conversion Factors: Conversion between units within the metric system is straightforward since they all relate by powers of 10.
💡 Note: Understanding these basics is the foundation for accurate conversions.
Basic Metric Conversions

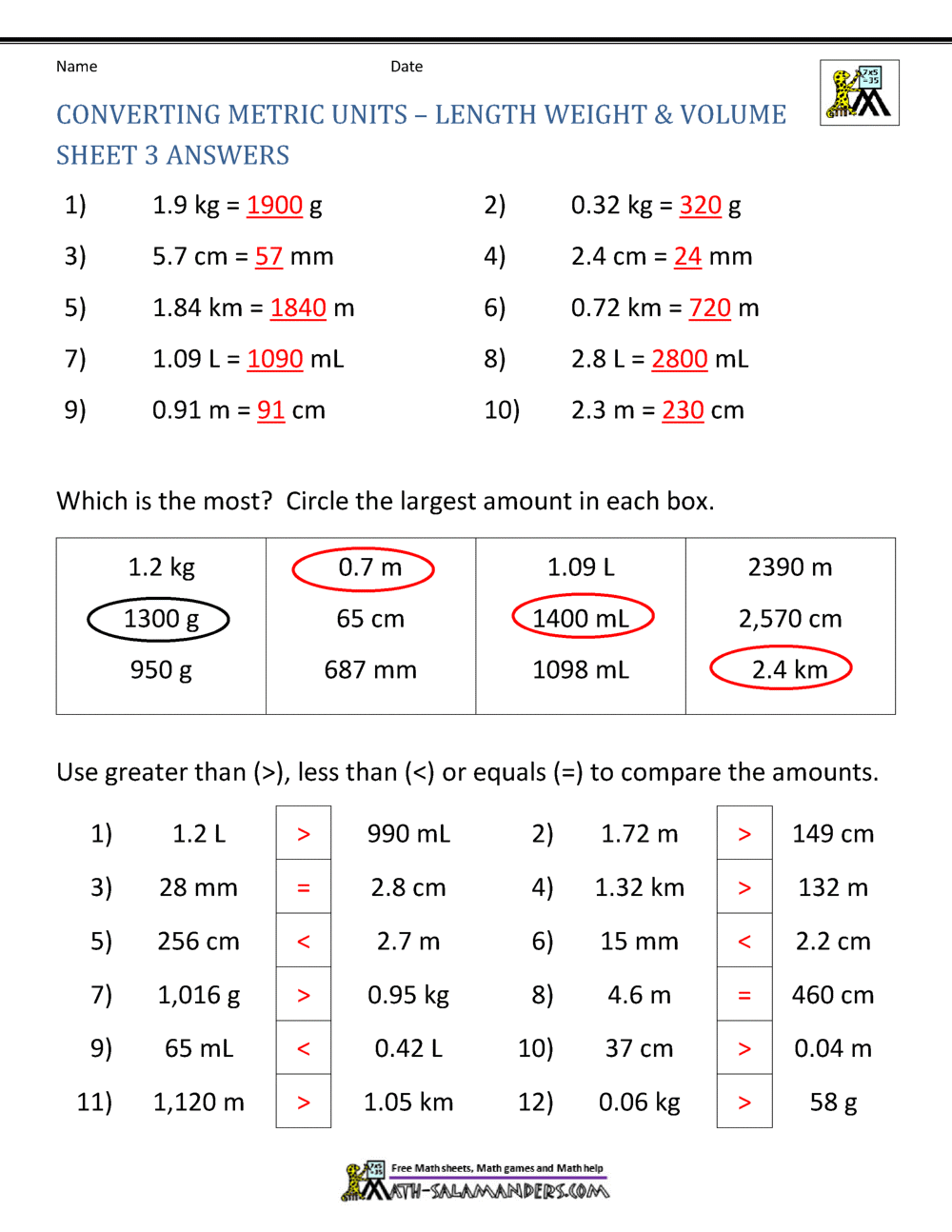
Let’s look at some basic metric conversions:
| From | To | Conversion |
|---|---|---|
| Kilogram (kg) | Gram (g) | 1 kg = 1000 g |
| Liter (L) | Milliliter (mL) | 1 L = 1000 mL |
| Meter (m) | Centimeter (cm) | 1 m = 100 cm |
| Meter (m) | Millimeter (mm) | 1 m = 1000 mm |

Detailed Conversion Examples

Now, let’s delve into some practical examples of converting between units:
Length

Converting meters to centimeters:
If you have a measurement of 5 meters, to convert it to centimeters: [ 5 \text{ meters} = 5 \times 100 \text{ cm} = 500 \text{ cm} ]Converting centimeters to kilometers:
For 7500 centimeters, the conversion to kilometers would be: [ 7500 \text{ cm} \div 100000 \text{ cm/km} = 0.075 \text{ km} ]
Mass

From kilograms to grams:
To convert 2.5 kilograms to grams: [ 2.5 \text{ kg} \times 1000 \text{ g/kg} = 2500 \text{ g} ]From grams to milligrams:
If you have 12 grams, converting to milligrams: [ 12 \text{ g} \times 1000 \text{ mg/g} = 12000 \text{ mg} ]
Volume

From liters to milliliters:
Converting 0.75 liters to milliliters: [ 0.75 \text{ L} \times 1000 \text{ mL/L} = 750 \text{ mL} ]From milliliters to cubic centimeters:
Since 1 mL is equivalent to 1 cubic centimeter: [ 250 \text{ mL} = 250 \text{ cc} ]
Temperature

Celsius to Fahrenheit:
To convert 25°C to Fahrenheit: [ 25°C \times \frac{9}{5} + 32 = 77°F ]Fahrenheit to Celsius:
Conversely, to convert 100°F to Celsius: [ (100°F - 32) \times \frac{5}{9} = 37.78°C ]
⏱️ Note: Always check the context or requirements of the conversion, as some industries or regions might have slightly different practices.
Strategies for Effective Conversion

To master metric conversions, here are some strategies:
- Understand the Prefixes: Familiarize yourself with the common prefixes and their values.
- Practice Regularly: Consistent practice helps ingrain conversion factors into your memory.
- Use Mnemonics: Create mnemonics or conversion charts for easy recall.
- Dimensional Analysis: Use the method of dimensional analysis to solve complex conversion problems by canceling out units.
📝 Note: Some learners find it helpful to use physical objects for scale understanding, e.g., comparing a liter bottle to visualize the volume.
Handling Conversion Errors

Mistakes in metric conversions can lead to errors in calculations. Here are some tips to avoid common mistakes:
- Double-Check Units: Ensure that the units you are converting to and from are correct.
- Understand Precision: Be mindful of significant figures and how rounding affects the accuracy of your conversion.
- Learn From Mistakes: If you encounter errors, take the time to understand where you went wrong.
- Use Conversion Tools: For complex or high-stakes conversions, consider using conversion tools or software for accuracy.
To sum it all up, mastering metric conversions is a journey of understanding, practice, and application. Whether you’re dealing with scientific research, engineering projects, or even everyday activities like cooking or traveling, a strong grasp of metric conversions ensures accuracy and efficiency. The examples and strategies provided should equip you with the tools needed to tackle any metric conversion problem you might come across. Remember, the key to success in this area is not just rote memorization but understanding the relationships between units and regular practice.
Why are metric conversions important?

+
Metric conversions are crucial for ensuring consistency in measurements across different regions and industries, facilitating global trade, scientific research, and ensuring standardization in various fields.
What’s the best way to practice metric conversions?

+
Practice regularly using conversion worksheets, real-life scenarios, or online conversion games. Understanding the system’s logic and consistency helps in making accurate conversions naturally.
How do I avoid common conversion mistakes?

+
Always double-check units, understand the precision required, use conversion tools when needed, and learn from past mistakes to improve accuracy.