Comparing Fractions Worksheet: Easy Guide
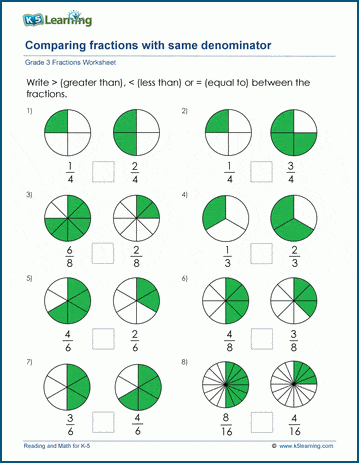
The concept of fractions is foundational in mathematics, and understanding how to compare fractions is critical for students to progress in their numerical literacy. This guide will explore what fractions are, why comparing them matters, and provide a Comparing Fractions Worksheet to enhance learning.
Understanding Fractions
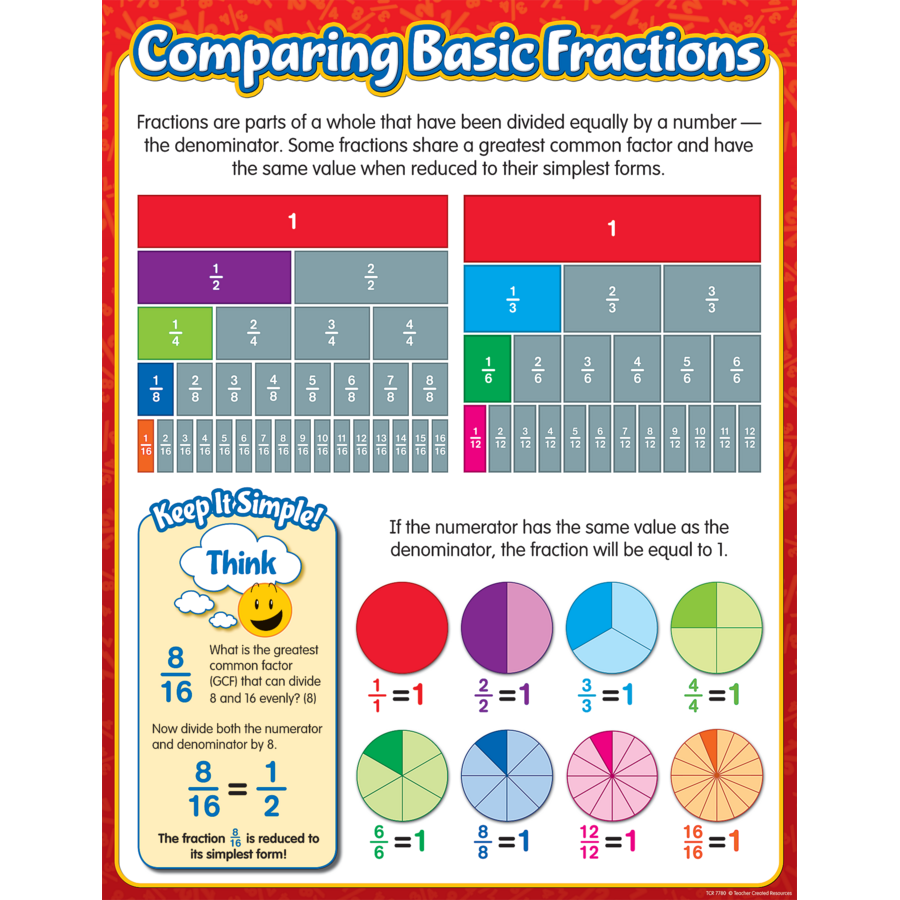
Fractions are essentially ways of representing parts of a whole or ratios between two numbers. They consist of a numerator (the top number) and a denominator (the bottom number). Here’s a simple breakdown:
- Numerator: The number of parts you have.
- Denominator: The total number of equal parts that make up the whole.

Why Compare Fractions?

Comparing fractions helps us understand size and equivalence, which are crucial for tasks like:
- Measuring ingredients in recipes.
- Analyzing statistical data in real-world scenarios.
- Solving mathematical problems and equations.
Methods to Compare Fractions
There are several methods to compare fractions:
1. Using a Common Denominator
The most common method is converting fractions to have a common denominator. Here’s how you do it:
- Find the least common denominator (LCD) of the fractions’ denominators.
- Multiply each fraction’s numerator and denominator by the same number to get the equivalent fraction with the LCD.
- Once fractions have the same denominator, compare their numerators directly.
💡 Note: The LCD can often be found using the lowest common multiple (LCM) of the denominators.
2. Cross-Multiplication

This method is useful for quick comparisons without finding a common denominator:
- Multiply the numerator of one fraction by the denominator of the other.
- Compare these products.
3. Visual Comparison with Diagrams

For visual learners or to teach younger students:
- Draw pie charts or bars where each fraction is represented.
- Compare the shaded areas to determine which fraction is larger.

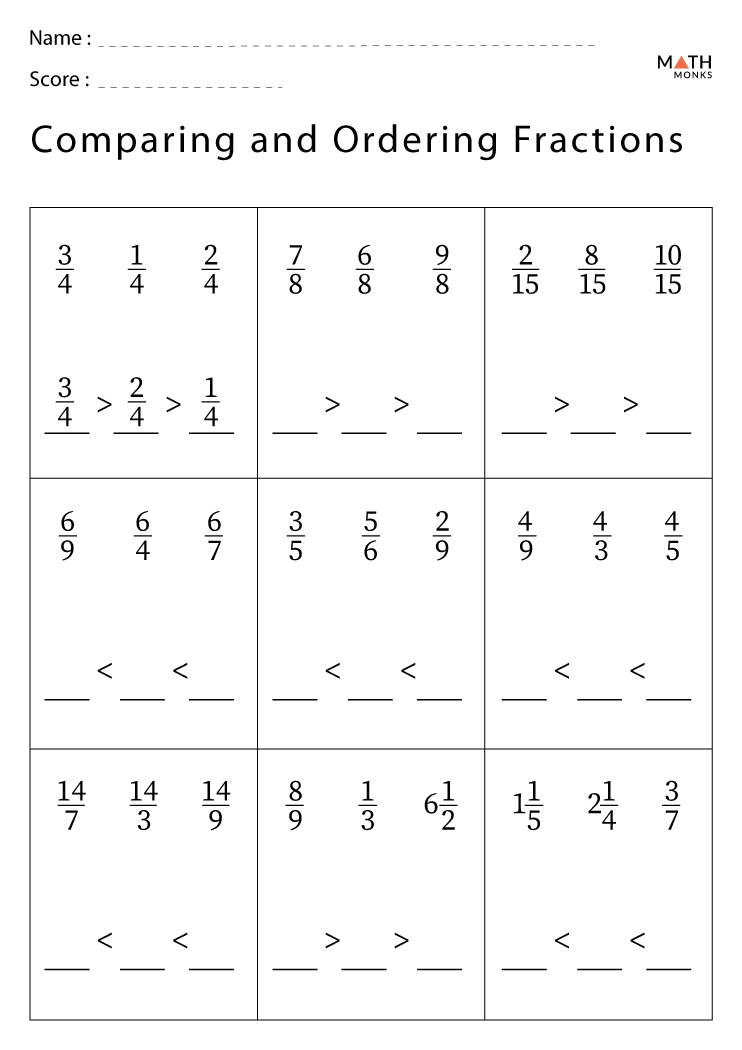
Comparing Fractions Worksheet

We’ve prepared a worksheet that incorporates these methods to make learning fun and practical:
| Fraction 1 | Fraction 2 | Method to Use | Which is Bigger? |
|---|---|---|---|
| 1⁄3 | 1⁄4 | Common Denominator | 1⁄3 |
| 2⁄5 | 3⁄5 | Direct Comparison | 3⁄5 |
| 4⁄6 | 5⁄8 | Cross-Multiply | 5⁄8 |

💡 Note: This worksheet covers a range of fractions from simple to complex, allowing students to practice different methods.
Teaching Tips for Comparing Fractions

Here are some tips for educators:
- Use real-life examples or props to make fractions tangible.
- Encourage students to use different methods to find which works best for them.
- Include exercises where students explain their reasoning to foster a deeper understanding.
Key Takeaways

Understanding how to compare fractions is essential for numeracy. By using various methods like common denominators, cross-multiplication, or visual aids, students can develop a strong foundation in mathematics. With practice worksheets and real-world applications, students will not only master comparing fractions but also appreciate the relevance of mathematics in daily life.
Why do we compare fractions?

+
Comparing fractions allows us to determine which part of a whole is larger or smaller, which is crucial in many real-life and academic scenarios, such as cooking, finance, and problem-solving in mathematics.
Can you compare fractions with different denominators without converting to a common denominator?
+
Yes, using methods like cross-multiplication or visual comparison can help compare fractions directly.
How can visual aids help in comparing fractions?

+
Visual aids like pie charts or bars help learners see the relative size of fractions, making it easier to understand and compare them.
Is there a specific age group recommended for teaching fraction comparison?

+
Fractions comparison is usually introduced in elementary school (around ages 6-10) but continues to be reinforced and expanded upon throughout higher education.