Solve Linear Equations and Inequalities with Ease

In today's digital age, mastering the art of solving linear equations and inequalities isn't just an academic requirement but a fundamental skill for a wide array of professionals. From engineers and scientists to financial analysts and computer programmers, understanding these concepts can provide significant advantages in problem-solving and decision-making processes. This blog post aims to guide you through the process, offering both a step-by-step tutorial and insights into the applications of these mathematical tools in real-world scenarios.
Understanding Linear Equations
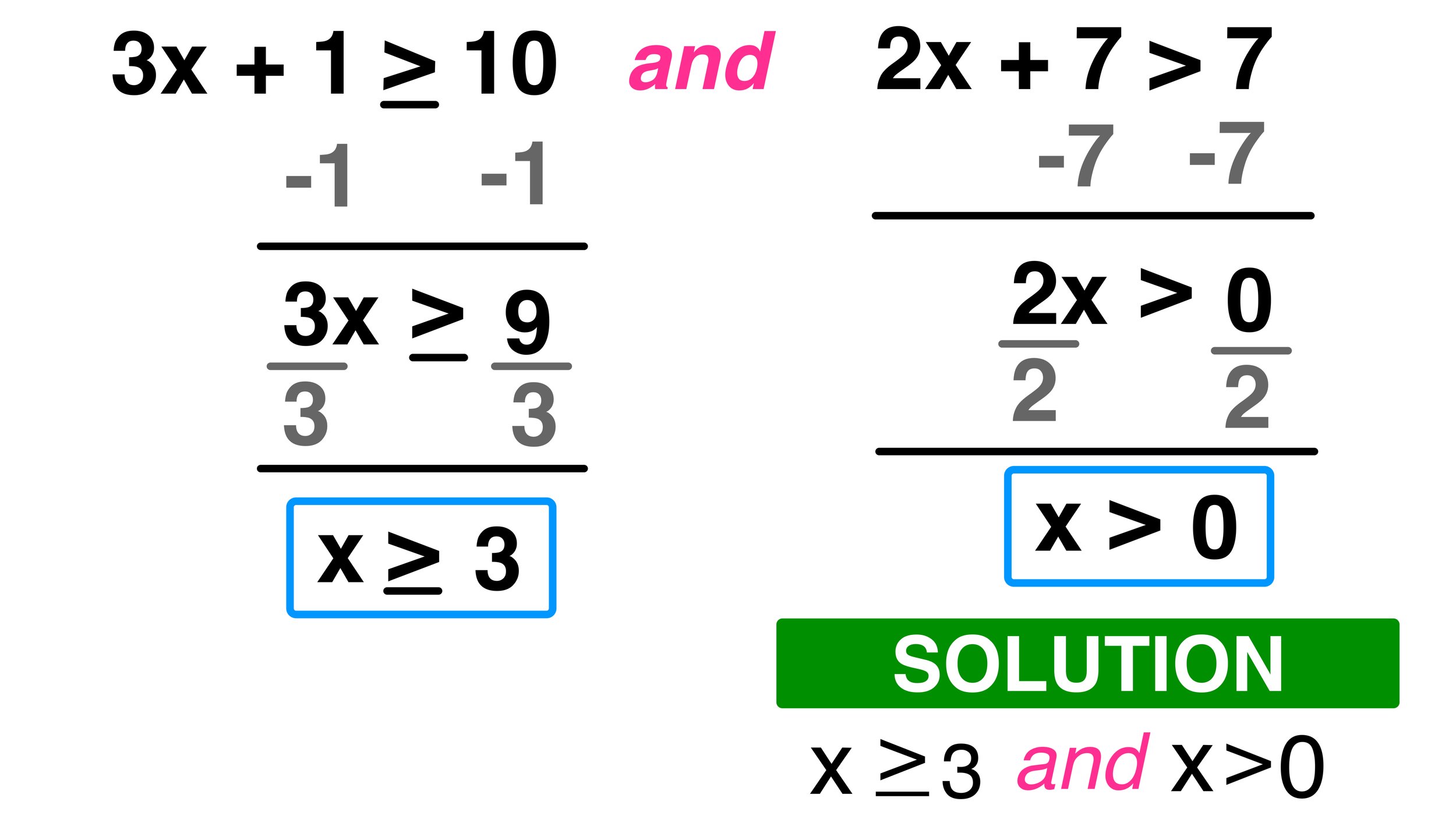
Linear equations are mathematical statements where the variable(s) appear only in their first power. Here's the general form:
ax + b = c
- a represents the coefficient of x.
- b is the constant term.
- c is the right-hand side of the equation, typically another constant term.
Steps to Solve Linear Equations

- Isolate the Variable: Use algebraic operations to move all terms with the variable (x) to one side and constants to the other.
- Divide or Multiply: Once x is isolated, perform division or multiplication to find the value of x.
Let's look at an example:
Solve for x: 3x + 4 = 16
- Step 1: Subtract 4 from both sides to isolate x:
3x + 4 - 4 = 16 - 4
3x = 12
- Step 2: Divide both sides by 3 to solve for x:
x = 12/3
x = 4
Here, the solution to the equation is x = 4. This means when x is 4, the equation holds true.
Checking Your Solution

After finding the value of x, it's a good practice to substitute it back into the original equation to verify that the equation balances:
3(4) + 4 = 16 12 + 4 = 16 16 = 16
If both sides of the equation are equal, your solution is correct.
🎯 Note: Always check your solution by substituting back into the equation. This can help catch any arithmetic errors.
Understanding Linear Inequalities

Unlike equations, inequalities describe a range where the expression on the left is either less than, less than or equal to, greater than, or greater than or equal to the expression on the right. Here's a table to show the differences:
| Symbol | Meaning |
|---|---|
| < | Less than |
| ≤ | Less than or equal to |
| > | Greater than |
| ≥ | Greater than or equal to |

Solving Linear Inequalities
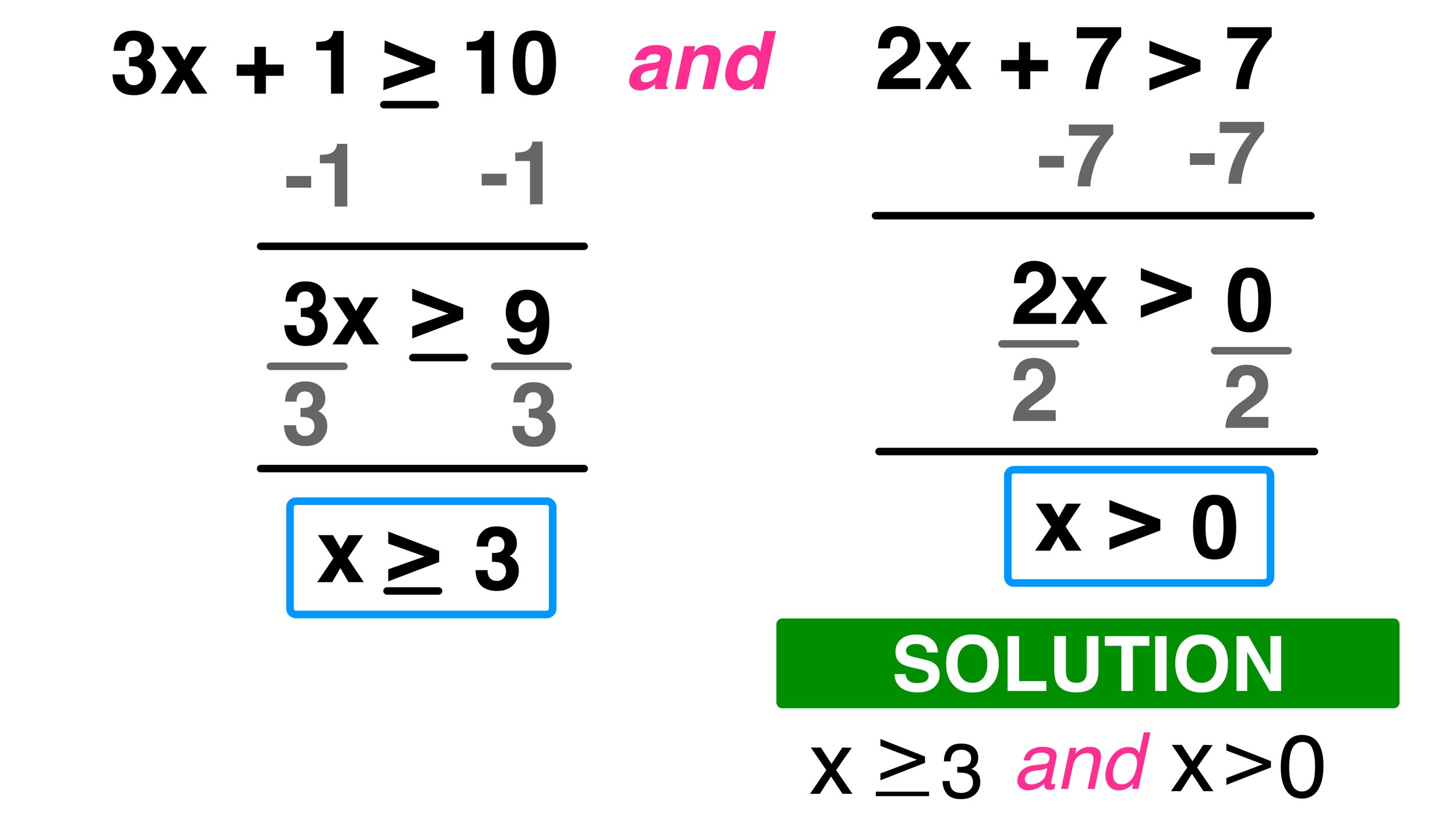
The process is similar to solving equations, but with one crucial difference:
- When multiplying or dividing both sides by a negative number, flip the inequality sign.
Here's how you might solve an inequality:
Solve for x: -2x + 7 > 3
- Step 1: Subtract 7 from both sides:
-2x + 7 - 7 > 3 - 7
-2x > -4
- Step 2: Divide both sides by -2, remembering to flip the inequality sign:
x < -4 / -2
x < 2
Here, the solution to the inequality means x can be any value less than 2.
Graphing Inequalities

Graphing inequalities provides a visual representation, aiding in understanding the solution set:
- Open circle for > or <, indicating that the value is not included.
- Filled circle for ≥ or ≤, indicating that the value is included.

🛑 Note: When plotting inequalities on a number line, remember to adjust your scale appropriately to fit the range of solutions.
Real-World Applications

Understanding linear equations and inequalities isn't just about solving academic problems; it has practical applications in various fields:
- Finance: Determining break-even points, calculating interest rates, or optimizing investment portfolios.
- Engineering: Designing systems, analyzing circuits, or optimizing resource allocation.
- Computer Science: Algorithm design, game theory, and optimization in machine learning.
The principles learned here are fundamental for many decision-making processes where one needs to find equilibrium, maximums, or minimums under given constraints.
Final Thoughts

In this exploration of linear equations and inequalities, we've covered how to approach and solve these mathematical statements. The ability to manipulate these expressions not only helps in academic contexts but also empowers individuals in their professional lives by fostering critical thinking and problem-solving skills. From the basic steps of isolating variables to understanding the nuances of inequalities, this knowledge forms a cornerstone of mathematical literacy, enhancing one's ability to navigate through complex scenarios with confidence and precision.
What are the key differences between linear equations and inequalities?

+
Linear equations aim to find a precise value where both sides are equal, while inequalities give us a range of values where one side is either greater than, less than, or equal to the other side. Additionally, when dividing or multiplying both sides of an inequality by a negative number, the inequality sign flips, which doesn’t happen with equations.
How can I make sure my solution to a linear equation is correct?

+
The most reliable method is to substitute your solution back into the original equation to see if both sides balance. If they do, your solution is likely correct.
Why do we flip the inequality sign when dividing or multiplying by a negative number?

+
Flipping the inequality sign ensures that the relative order of the values remains consistent. If you multiply or divide both sides by a negative number, the inequality becomes reversed because you are essentially inverting the values, which changes the direction of the comparison.



