Unlock Math Skills: Mastering Inverse Functions Worksheet 7.4

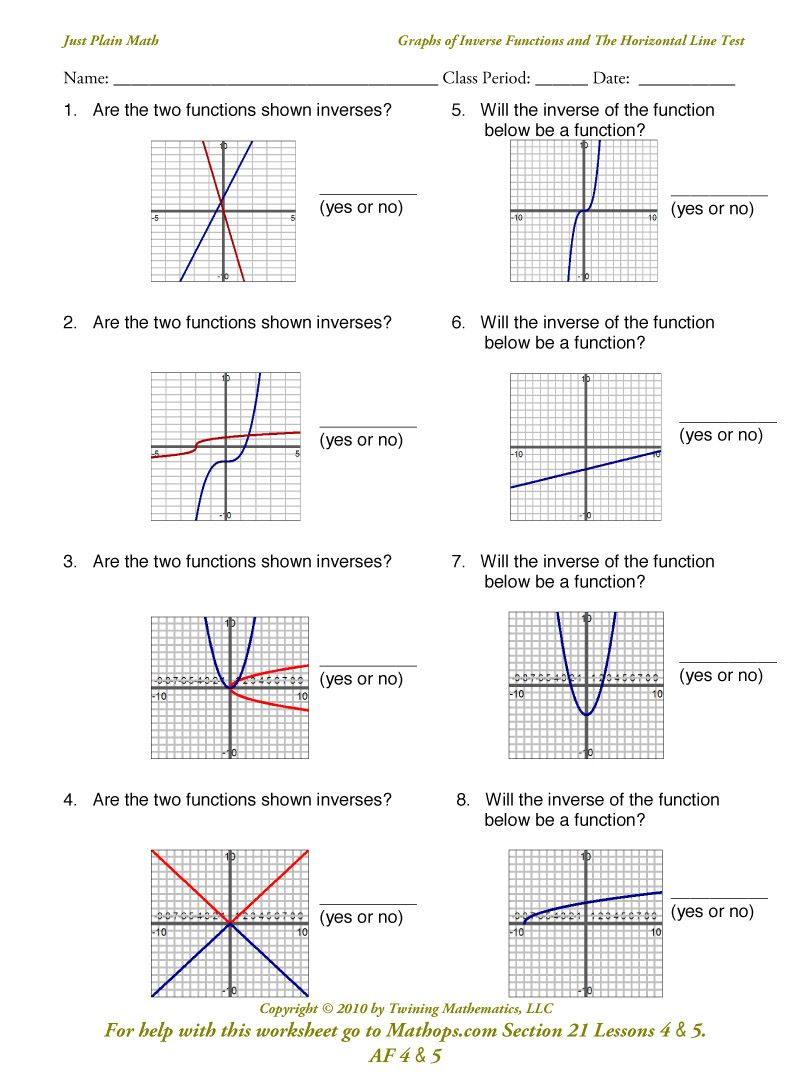
The beauty of mathematics often lies in its symmetry and balance, and nowhere is this more evident than in the study of functions and their inverses. If you're on a journey to deepen your understanding of inverse functions, this guide aims to be your compass. Today, we'll explore Inverse Functions Worksheet 7.4, tailored to help students unlock the secrets behind these crucial mathematical relationships.

Understanding Inverse Functions

Inverse functions are like the mathematical equivalent of two dancers moving in perfect sync. Each step of one function corresponds inversely to the steps of its counterpart. Here are the essentials:

• Definition: An inverse function reverses what the original function does. If (f(x)) maps (a) to (b), then (f^{-1}(x)) maps (b) back to (a).
• Properties:
  • If (f(x)) is a one-to-one function (no two elements of the domain map to the same element in the codomain), it has an inverse.
  • (f(f^{-1}(x)) = f^{-1}(f(x)) = x), this property showcases the function-inverse relationship.
• Graphical Insight: The graph of (f^{-1}(x)) is a reflection of (f(x)) over the line (y = x).

Diving into Worksheet 7.4

Worksheet 7.4 is designed to reinforce understanding through practical application. Here’s what you’ll find:

• Problem Types:
  • Find inverse functions algebraically.
  • Verify that two functions are inverses of each other.
  • Sketch and interpret the graphs of inverse functions.
  • Solve real-world problems involving inverse functions.
• Learning Objectives:
  • Enhance problem-solving skills.
  • Understand how inverse functions operate within practical contexts.

Steps to Solve Inverse Function Problems

Let’s break down the steps to solve inverse function problems:

1. Determine If a Function is One-to-One: This can be done via the horizontal line test or by verifying uniqueness in function output.
2. Find the Inverse Function:
   • Replace (f(x)) with (y).
   • Swap (x) and (y).
   • Solve for (y) to obtain the inverse (f^{-1}(x)).
   • Ensure the domain of (f^{-1}(x)) matches the range of (f(x)).
3. Verify Inverses: If two functions (f) and (g) are suspected to be inverses, check if (f(g(x)) = g(f(x)) = x).
4. Graphing Inverses: Reflect the graph of (f(x)) over (y=x) to visualize (f^{-1}(x)).

Solving Example Problems

Let’s delve into an example from Worksheet 7.4 to clarify how to approach these problems:

• Example 1: Finding the Inverse Algebraically:

  Given (f(x) = 3x - 2), find (f^{-1}(x)).

  1. Set (y = 3x - 2).
  2. Swap (x) and (y) to get (x = 3y - 2).
  3. Solve for (y): [ x + 2 = 3y \Rightarrow y = \frac{x + 2}{3} ]
  4. So, (f^{-1}(x) = \frac{x + 2}{3}).
• Example 2: Verifying Inverses:

  Given (f(x) = 2x + 1) and (g(x) = \frac{x - 1}{2}), verify they are inverses.

  1. Check (f(g(x))): [ f(g(x)) = f\left(\frac{x - 1}{2}\right) = 2\left(\frac{x - 1}{2}\right) + 1 = x - 1 + 1 = x ]
  2. Check (g(f(x))): [ g(f(x)) = g(2x + 1) = \frac{2x + 1 - 1}{2} = \frac{2x}{2} = x ]
  3. Since both (f(g(x)) = g(f(x)) = x), (f) and (g) are inverses.

Strategies for Learning Success

Here are some tips to maximize your learning from Worksheet 7.4:

• Practice Regularly: Frequent engagement with inverse function problems can solidify your understanding.
• Use Visualization: Graphing helps to visualize the relationship between a function and its inverse.
• Collaborate: Discussing problems with peers can offer new insights and methods for solving.
• Reflect on Mistakes: Analyze where you went wrong and how to correct it.

🔑 Note: Always check if the function is one-to-one before attempting to find its inverse. A common mistake is assuming all functions have inverses.

Applications of Inverse Functions

Inverse functions have profound impacts in various fields:

• Encryption and Cryptography: Understanding inverse functions is crucial in encoding and decoding messages.
• Physics and Engineering: They’re used for solving problems involving inverse kinematics or reversing the effects of forces.
• Economics: Demand functions and their inverses help analyze market equilibrium.
• Health and Medicine: Understanding dosage-response relationships through inverse modeling.

As we reach the end of our exploration into mastering inverse functions with Worksheet 7.4, let’s recap some key insights:

• Inverse functions undo the effect of their original functions, creating a symmetrical relationship.
• They are crucial in various problem-solving and analytical contexts, offering a deeper understanding of mathematical relationships.
• Worksheet 7.4 provides practical exercises to master these concepts, enhancing both algebraic skills and problem-solving abilities.
• Consistency, visualization, and reflective learning are pivotal for success in mastering these mathematical tools.

Why are inverse functions important in mathematics?

+

Inverse functions help to understand and solve various mathematical problems by allowing us to reverse the operations performed by other functions, enhancing the symmetry and balance in mathematical relationships.

What’s the first step to find the inverse of a function?

+

The first step is to check if the function is one-to-one, meaning no two elements of the domain map to the same element in the codomain. This can be done through the horizontal line test or by ensuring each input has a unique output.

Can every function have an inverse?

+

Not every function has an inverse. Only one-to-one functions (injective functions) can have an inverse, as this property ensures that the inverse will also be a function.