5 Easy Steps to Master Composite Shapes Worksheets

Understanding Composite Shapes
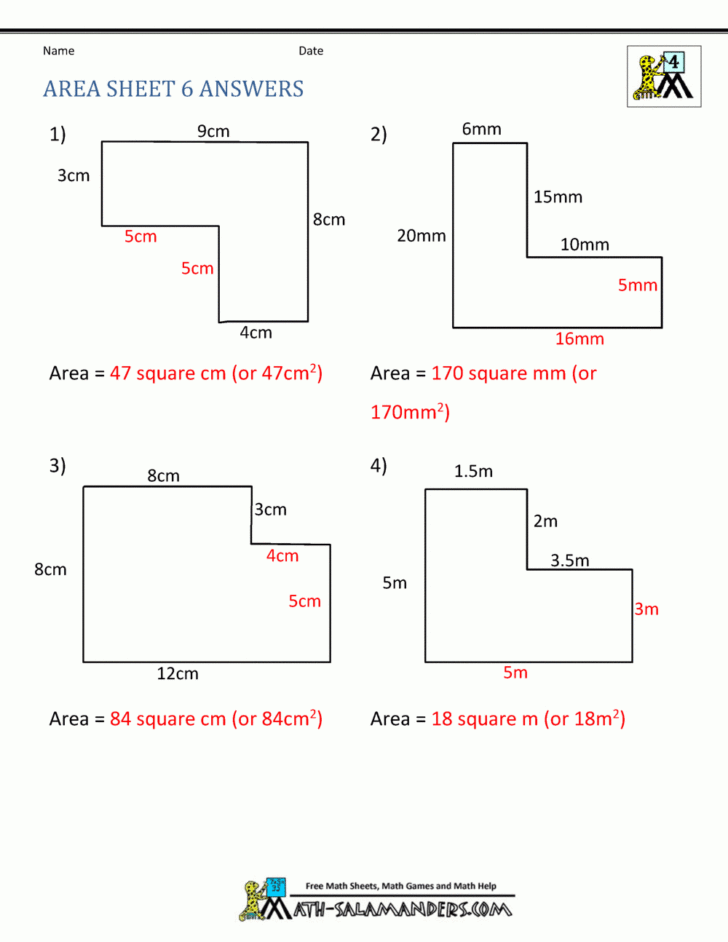
Before delving into the art of mastering composite shapes, let’s establish a foundational understanding of what they are. A composite shape, also known as a compound shape, is a combination of two or more simpler shapes. These shapes can be circles, rectangles, triangles, or any other basic geometric figures. The idea is to break down these intricate figures into recognizable pieces, enabling us to analyze them more efficiently.
Learning to dissect and comprehend composite shapes not only boosts our spatial intelligence but is also crucial in fields like architecture, engineering, and mathematics. Here's a glimpse into how these shapes work:
- They are often used in real-life scenarios for land surveying, architectural planning, and art projects.
- Calculating the area or perimeter of composite shapes requires the knowledge of how to manage multiple simpler shapes within one.
- Understanding composite shapes helps in abstract thinking and logical problem-solving.
Step 1: Identifying Simple Shapes


The first step in mastering composite shapes is to spot the simpler shapes within the complex one. When you see a composite shape:
- Look for straight lines, angles, or curves that suggest familiar figures like rectangles, squares, triangles, or circles.
- Use visual cues like lines of symmetry or overlapping areas to guide your identification.
- Sometimes drawing auxiliary lines can make the shapes more visible.
💡 Note: Not all composite shapes are symmetrical or easily recognizable, which makes this step particularly challenging but also rewarding.
Step 2: Breaking Down the Shapes

Once the simple shapes within the composite shape have been identified, proceed to break them down:
- Draw lines (either virtually or physically) to separate the shapes where they intersect or overlap.
- Label each identifiable part with its respective shape name to streamline your thinking.
- Note the dimensions or characteristics of each sub-shape for further calculations.
Here's a simple example:
| Shape | Dimensions |
|---|---|
| Rectangle | Length: 6 units, Width: 4 units |
| Triangle | Base: 6 units, Height: 4 units |
✅ Note: Breaking down shapes into their basic components makes further calculations much easier, as you'll be dealing with known formulas.
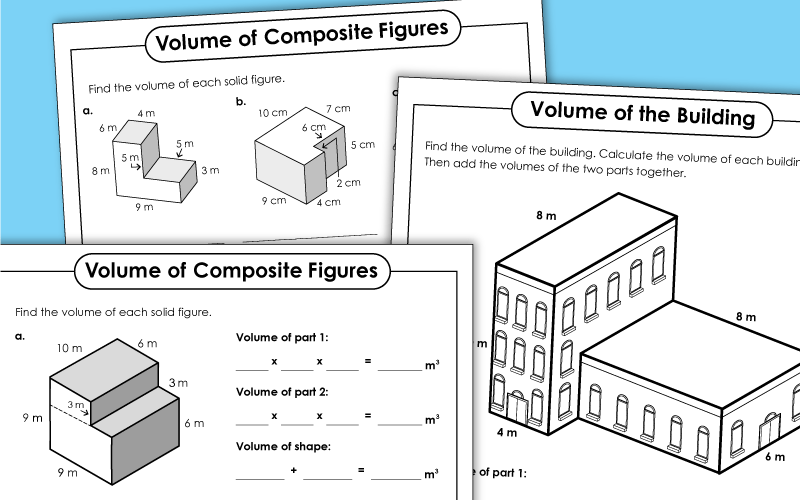
Step 3: Calculating Area


With the shapes identified and dimensions noted, the next step is calculating the area:
- Calculate the area of each simpler shape using their respective formulas:
- Area of a rectangle: Length × Width
- Area of a triangle: (Base × Height) / 2
- Area of a circle: π × Radius²
- Sum or subtract the areas of these shapes based on how they are arranged within the composite shape.
- Keep in mind the orientation of shapes, as it can affect the calculation, especially for triangles and trapezoids.
Step 4: Finding Perimeter
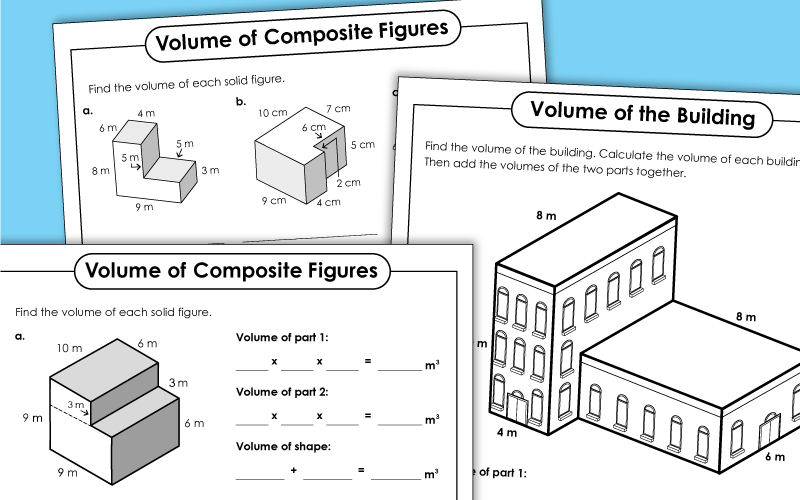
The perimeter of composite shapes can be a bit trickier:
- Identify which sides form the perimeter of the entire shape, which might involve leaving out internal lines.
- Add the lengths of these external sides together, and be mindful of any common sides shared by adjacent shapes.
- If there are circular segments, remember to add the arc length.
📏 Note: Perimeter calculation involves careful analysis of which sides are external, making it different from area calculation.
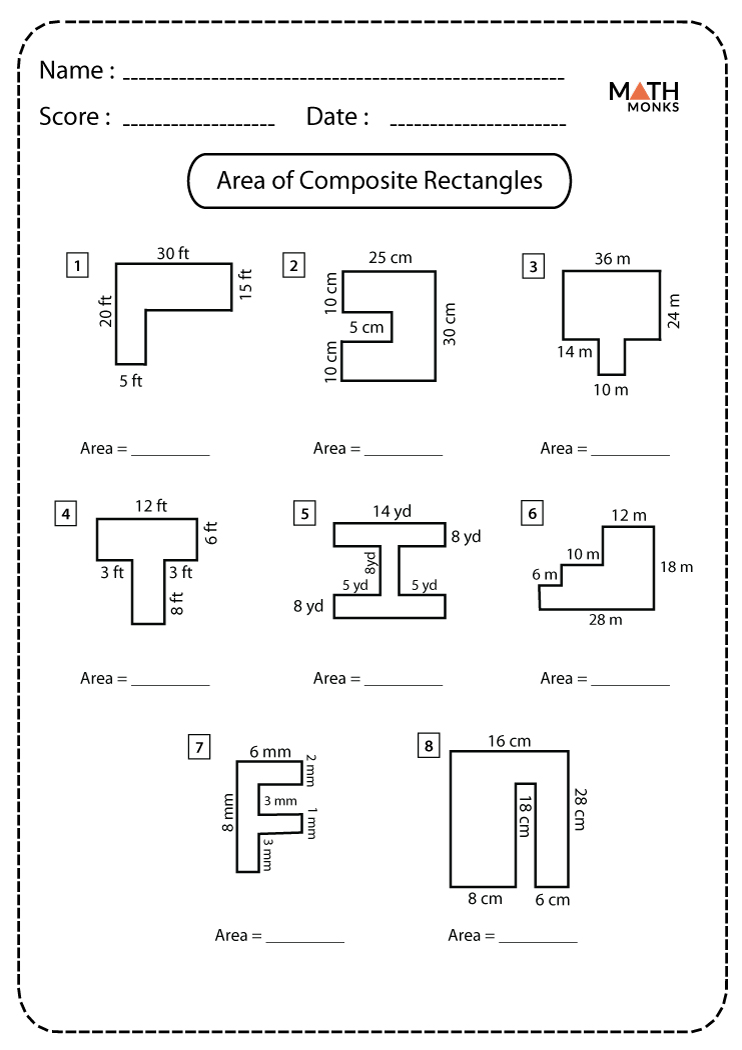
Step 5: Practice with Composite Shape Worksheets

The final step in mastering composite shapes is consistent practice:
- Look for composite shape worksheets online or in math workbooks.
- Start with simpler composite shapes and gradually move to more complex ones as you become more confident.
- Use graph paper for precision in breaking down and calculating shapes.
- Check your answers, learn from mistakes, and repeat the process to enhance proficiency.
Mastering these steps through regular practice will significantly improve your grasp on composite shapes. Not only will it become second nature, but it'll also enhance your overall mathematical ability.
As we conclude this journey into mastering composite shapes, remember that the skills you acquire here are foundational for many higher-level math concepts. Whether it’s for professional growth, academic advancement, or personal curiosity, the ability to break down complex figures into manageable parts and analyze them mathematically is an invaluable tool. With practice, you’ll find these shapes becoming less intimidating, and the principles behind them more intuitive.
Why are composite shapes important in mathematics?
+
Composite shapes encourage problem-solving skills, logical thinking, and understanding of spatial relationships. They are fundamental in geometry and have practical applications in fields like engineering, architecture, and design.
How do I identify shapes within a composite shape?

+
Look for clear lines, angles, or circular curves. Break the shape down into simpler forms by drawing auxiliary lines and identifying symmetrical or overlapping areas.
Can I calculate the area of composite shapes with different units of measurement?

+
Yes, but ensure all measurements are converted to the same unit before calculations to maintain consistency.


