7 Tips for Mastering LCM and GCF Worksheets

7 Tips for Mastering LCM and GCF Worksheets

Mathematics, especially number theory, often presents challenging concepts like the Least Common Multiple (LCM) and the Greatest Common Factor (GCF). These foundational concepts are not only crucial for understanding algebra but are also frequently tested in various exams and standardized tests. Here, we delve into seven strategic tips to help students master LCM and GCF worksheets.
Tip 1: Understand the Basics

Before diving into complex problems, ensuring a solid foundation in the definitions is critical:
- Greatest Common Factor (GCF): The largest number that divides all numbers without a remainder. It's also known as the Greatest Common Divisor (GCD).
- Least Common Multiple (LCM): The smallest number that is a multiple of two or more numbers.
Example: For numbers 12 and 18, the GCF is 6, and the LCM is 36.
Tip 2: Use Prime Factorization

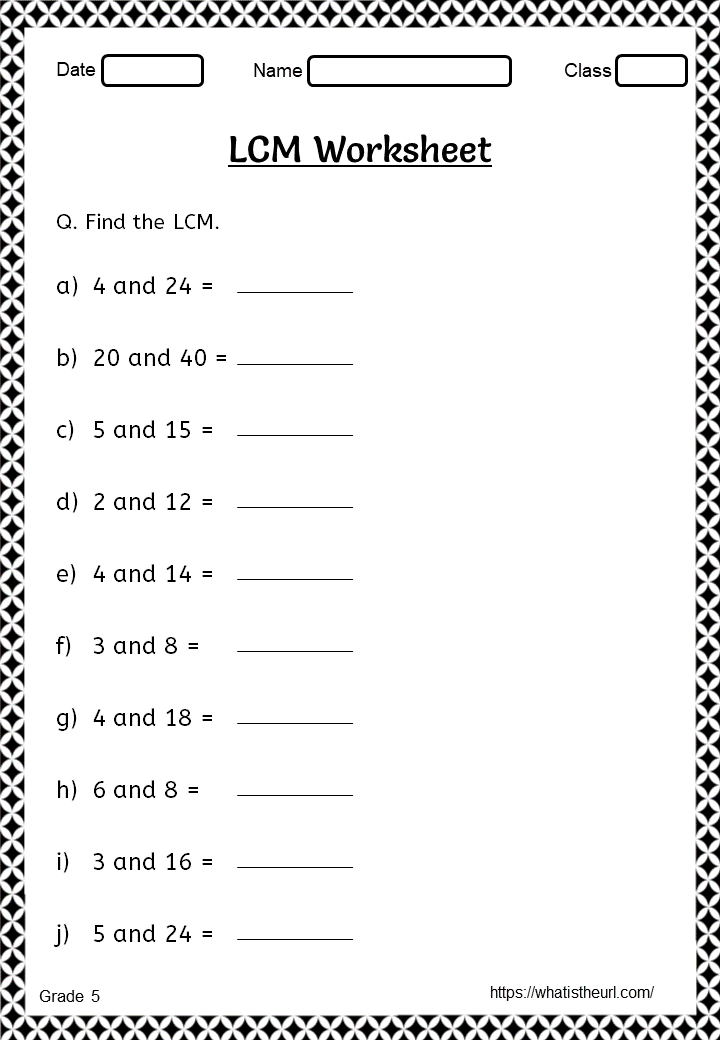
Prime factorization is a foolproof method for calculating both GCF and LCM. Here's how to do it:
- GCF: Multiply all the lowest powers of common prime factors.
- LCM: Take the highest power of all prime factors present in any of the numbers.
Example: For numbers 24 (23 * 3) and 36 (22 * 32),
- GCF = 22 * 3 = 12
- LCM = 23 * 32 = 72
💡 Note: Mastering prime factorization can significantly speed up your calculations for GCF and LCM.
Tip 3: Practice with Real-life Scenarios

Applying LCM and GCF in real-life scenarios can help solidify understanding:
- Syncing Meeting Schedules: Use LCM to find the earliest common time all parties can meet.
- Gardening: If you have different plants that need watering on different days, use LCM to find the least often you'll need to water all plants at the same time.
Tip 4: Learn Shortcuts

While prime factorization is thorough, there are shortcuts for simpler numbers:
- For GCF, you can find common factors through division.
- For LCM, you can multiply the two numbers and divide by their GCF.
Tip 5: Use Visual Aids
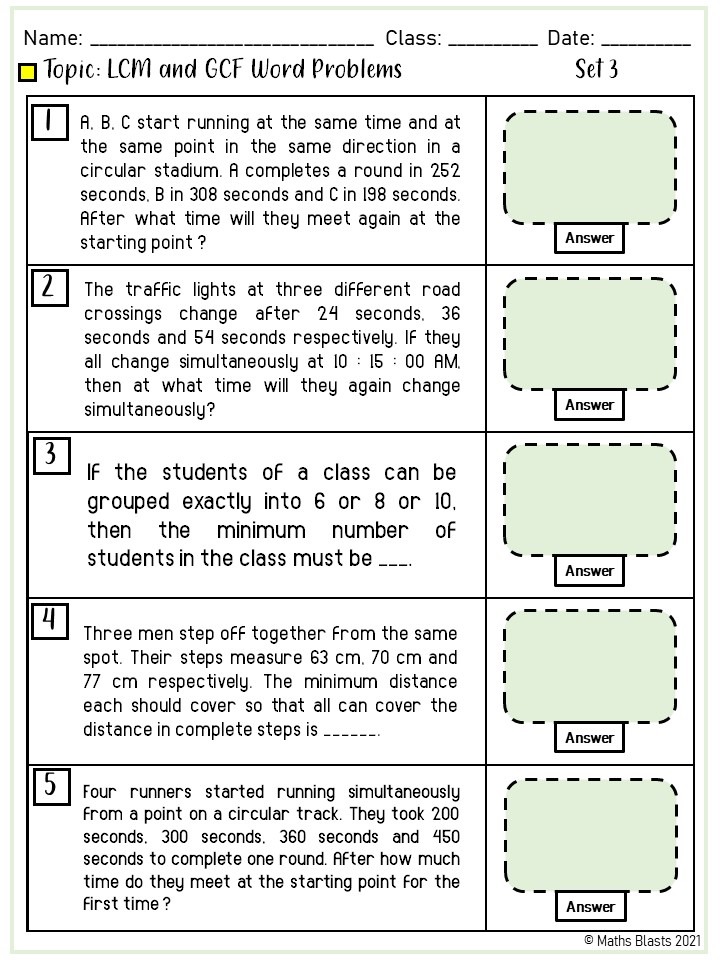
Visual aids like Venn diagrams can visually represent the overlap of factors between numbers:
| Prime Factor | Number A | Number B | GCF | LCM |
|---|---|---|---|---|
| 2 | 23 | 22 | 22 | 23 |
| 3 | 3 | 32 | 3 | 32 |
| LCM | 72 |

Tip 6: Relate LCM and GCF
There's a fundamental relationship between GCF and LCM that can be expressed as:
LCM(a, b) * GCF(a, b) = a * b
This relationship can be handy in checking calculations.
Tip 7: Regular Revision and Practice

Consistent practice is key to mastering these concepts:
- Regularly work on LCM and GCF problems.
- Use worksheets that are progression-based, starting from easy to complex problems.
- Review the theory every time you start a new worksheet.
🛠️ Note: Continuous practice and revisiting the basics are essential for mastering mathematical concepts.
Mastering LCM and GCF is not just about understanding these calculations but also about applying them effectively in various contexts. Whether you're solving a math puzzle, planning a schedule, or even dealing with fractions and ratios, these skills are indispensable. Through understanding the basics, using effective techniques like prime factorization, applying shortcuts, and engaging with visual tools, students can achieve proficiency in LCM and GCF calculations. The journey from basic arithmetic to complex problem-solving requires patience, practice, and a curious mind ready to explore the beauty of numbers.
Why is it important to master LCM and GCF?

+
Mastering LCM and GCF is essential because they are foundational concepts in algebra, number theory, and various applications in real-life scenarios like scheduling, measuring, and optimization.
Can LCM and GCF be calculated for more than two numbers?

+
Yes, LCM and GCF can be calculated for any number of integers, though the process can become more complex as more numbers are involved.
What are some common mistakes when calculating LCM and GCF?

+
Common mistakes include:
- Not identifying all prime factors correctly.
- Multiplying prime factors incorrectly.
- Missing the relationship between LCM and GCF when checking answers.