5 Easy Worksheets to Master Circle Parts

Learning about the parts of a circle is fundamental for anyone studying geometry. Circles are not just simple curves; they embody intricate mathematical concepts and properties that are essential for understanding more complex geometric theories. In this detailed guide, we will explore various worksheets designed to help you master the different parts of a circle through both visual and mathematical exercises.
Why Understanding Circle Parts Matters
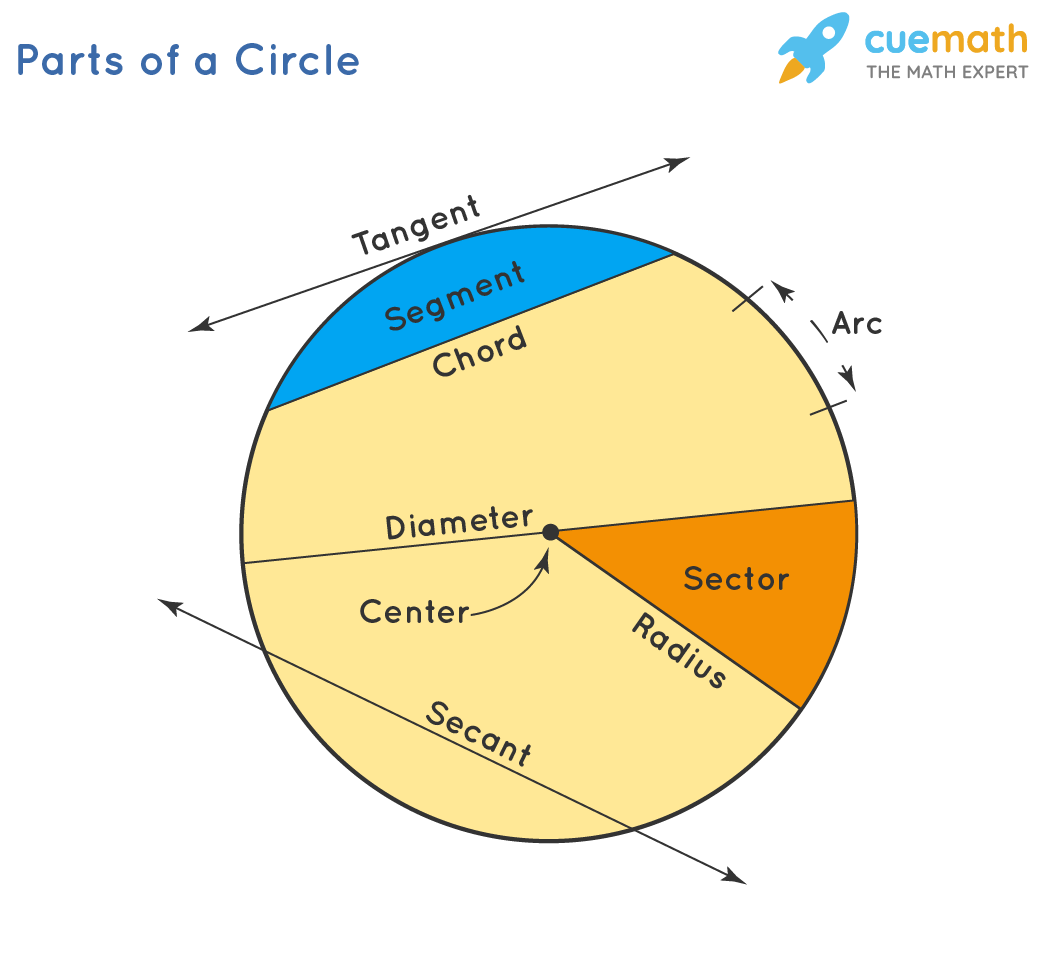
Before we delve into the worksheets, let’s briefly understand why learning about circle parts is crucial:
- Fundamental Math Knowledge: Circles are ubiquitous in mathematics, from basic algebra to calculus, understanding circle parts aids in grasping concepts like the Pythagorean theorem, area, and circumference formulas.
- Practical Applications: Circles appear in everyday life, from wheels and round objects to the design of optical instruments, thus, understanding their parts has real-world applications.
- Base for Further Studies: Circle geometry forms the groundwork for trigonometry, coordinate geometry, and even astrophysics.
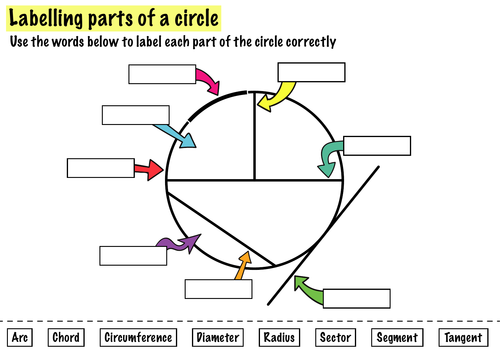
Worksheet 1: Identifying and Labeling Circle Parts

The first step in mastering circle parts is to learn how to identify and label them correctly:
- Draw a perfect circle.
- Label the center, radius, diameter, chord, secant, arc, and segment.
🏫 Note: Use a ruler to draw straight lines for diameter and chord; this will help in visualization and accuracy.

Worksheet 2: Measuring and Calculating Circle Properties
In this worksheet, we go beyond identification to practice measurement and calculation:
- Measure the diameter and calculate the radius.
- Use the formula to calculate the circumference and area.
- Identify and measure the length of a chord, arc, and segment.
| Circle Property | Measurement/Formula |
|---|---|
| Diameter (D) | Measure directly or calculate twice the radius (2R) |
| Radius ® | Measure directly or calculate D/2 |
| Circumference © | 2πR |
| Area (A) | πR2 |

📚 Note: Ensure students understand the use of the Greek letter pi (π) which is approximately 3.14.
Worksheet 3: Circle’s Arc and Sector

Here we focus on arcs and sectors:
- Define and identify a major and minor arc.
- Calculate arc lengths and areas of sectors.
Example Problem: If the radius of a circle is 7 cm and the central angle of an arc is 60°, find the length of the arc and the area of the sector.
Steps:
- Calculate arc length: (60⁄360) * 2π * 7 = (1⁄6) * 14π ≈ 7.33 cm
- Calculate sector area: (60⁄360) * π * 72 = (1⁄6) * 49π ≈ 25.65 cm2
Worksheet 4: Chords and Segments

Delving into the properties of chords and segments:
- Identify perpendicular and bisecting chords.
- Calculate segment areas using chord properties.
Worksheet 5: Circle Theorems and Proofs

Finally, we explore circle theorems which require logical proofs:
- Prove that the angle at the center is twice the angle at the circumference.
- Prove the perpendicular bisector theorem for chords.
- Explore other circle theorems like the tangent-secant theorem.
In wrapping up our journey through the world of circles, we can appreciate how these seemingly simple shapes hold a wealth of knowledge and application. Each worksheet not only deepens our understanding but also sharpens our problem-solving skills, mathematical accuracy, and logical thinking. By mastering these concepts, we've taken a significant step towards understanding one of geometry's most fundamental shapes, opening up a world of mathematical exploration.
What are the key parts of a circle?

+
The key parts of a circle include the center, radius, diameter, chord, arc, segment, and tangent.
How can I calculate the circumference of a circle?

+
The circumference © can be calculated using the formula: C = 2π * Radius, where π is approximately 3.14159.
Why is learning about circle parts important in geometry?

+
Understanding circle parts is crucial because they form the basis for many geometrical calculations, from basic area and circumference formulas to advanced topics like trigonometry and calculus.