Kuta Functions Worksheet: Master Math with Ease

Welcome to an exhilarating exploration of functions in mathematics, where we'll delve into the world of Kuta functions to ensure that math becomes not just a subject to learn but an adventure to embrace. Whether you're a student seeking clarity or an educator looking for effective teaching strategies, this comprehensive guide will equip you with the tools necessary to master functions with ease.
Understanding Functions

In the realm of mathematics, a function is a rule or correspondence between two sets that assigns to each element of the first set exactly one element of the second set. Here, we will break down what that means:
- Domain: The set of all possible input values, commonly represented as x .
- Range: The set of all output values resulting from the function, usually y .
- Function Notation: Functions can be expressed in several notations like f(x) or y = f(x) .
Let's visualize this with an example:

Types of Functions

Functions can vary widely in their behavior and presentation:
- Linear Functions: These are functions of the form f(x) = mx + b , where m is the slope and b the y-intercept.
- Quadratic Functions: Represented as f(x) = ax^2 + bx + c , they often form a parabola.
- Exponential Functions: These functions grow or decay exponentially, f(x) = ab^x .
- Polynomial Functions: These are sums of terms like f(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0 .
Evaluating and Simplifying Functions
Let's delve into how to evaluate and simplify functions:
Evaluating Functions

To evaluate a function for a specific x , you simply substitute the value into the function:
f(x) = 2x + 3
f(4) = 2 * 4 + 3 = 11
Simplifying Functions

Algebra can make functions more manageable:
f(x) = x^2 + 4x + 4
Simplify: f(x) = (x + 2)^2
💡 Note: Simplifying functions can reveal underlying structures, making problem-solving more efficient.
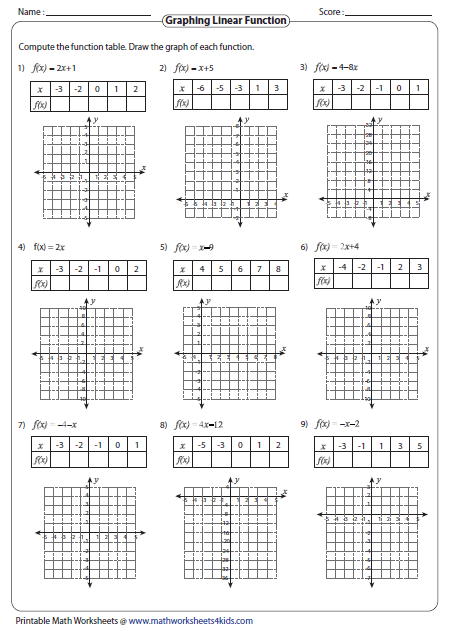
Creating and Using Function Tables

Function tables are an excellent visual aid. Here's an example of how to create one:
| x | f(x) = 2x + 3 |
|---|---|
| 0 | 3 |
| 1 | 5 |
| 2 | 7 |

🔍 Note: Function tables help in identifying patterns and behavior in functions over a range of inputs.
Applications of Functions in Real Life

Functions aren't just theoretical; they have real-world applications:
- Economics: Cost and revenue functions to determine profit.
- Physics: Displacement, velocity, and acceleration functions in kinematics.
- Computer Science: Algorithms that map inputs to outputs.
Mastering Functions with Kuta Software

Kuta Software provides an invaluable tool for practicing functions:
- Function Worksheets: Offering various levels of complexity for different age groups.
- Interactive Activities: Allows for immediate feedback and correction.
- Customization: Tailor worksheets to match specific learning objectives or student needs.
Strategies for Teaching Functions

When teaching functions, consider these strategies:
- Concrete-Representational-Abstract (CRA) Sequence: Start with concrete examples, move to representations, then abstract concepts.
- Graphical Interpretation: Use graphing calculators or software to visualize functions.
- Word Problems: Relate functions to real-world scenarios to enhance understanding.
🌟 Note: A multi-sensory approach to teaching functions can lead to better retention and application.
In summary, this journey through functions has provided you with a comprehensive understanding of the subject. From recognizing the basic concepts, evaluating, and simplifying, to applying functions in practical scenarios, we’ve covered key elements that will help both students and educators navigate the intricacies of functions with confidence. Remember, functions are not just formulas; they are tools that help us describe the world around us in precise mathematical terms, making them an essential part of mathematical literacy.
What is the domain of a function?
+
The domain of a function is the complete set of possible values for the independent variable (commonly ( x )) that makes the function work, and provides real outputs for ( f(x) ).
How can I simplify a quadratic function?
+
To simplify a quadratic function, you can complete the square, which involves taking the coefficient of ( x ), dividing by 2, squaring the result, and adding/subtracting it from the function to form a perfect square trinomial.
What is the significance of the function notation ( f(x) )?
+
The function notation ( f(x) ) represents how the function ( f ) acts on the input ( x ). It’s a shorthand way to denote the relationship between ( x ) and the output, making it easier to refer to and manipulate the function in mathematical expressions.
Why is understanding functions important?

+
Functions are fundamental in mathematics, science, engineering, and finance as they help model relationships, predict outcomes, solve problems, and understand dynamic systems.



