Kinematic Curves Worksheet: Mastering Motion Analysis

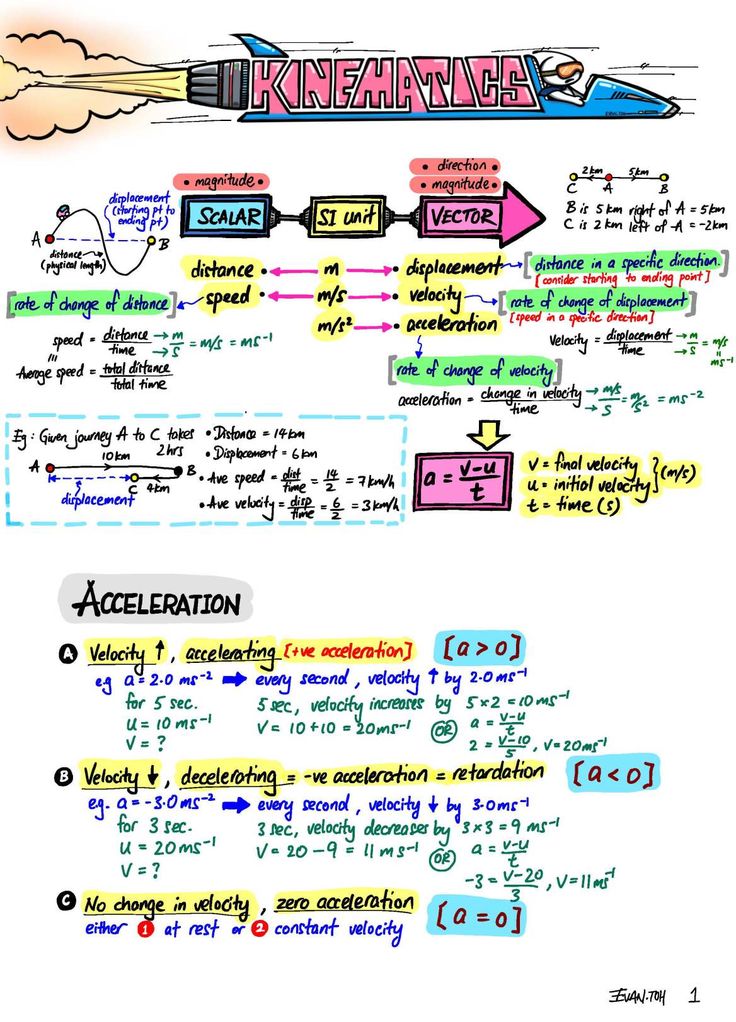
The realm of physics that examines the motion of objects, without consideration of the forces causing that motion, is known as kinematics. In this field, understanding kinematic curves is essential as they provide a graphical representation of motion. Whether you're a student, a teacher, or just an enthusiast of physics, this worksheet on Kinematic Curves will guide you through the process of mastering motion analysis.
Understanding Kinematic Curves
Kinematic curves are graphical plots that depict position, velocity, and acceleration over time. Each type of kinematic curve offers unique insights into an object's motion:
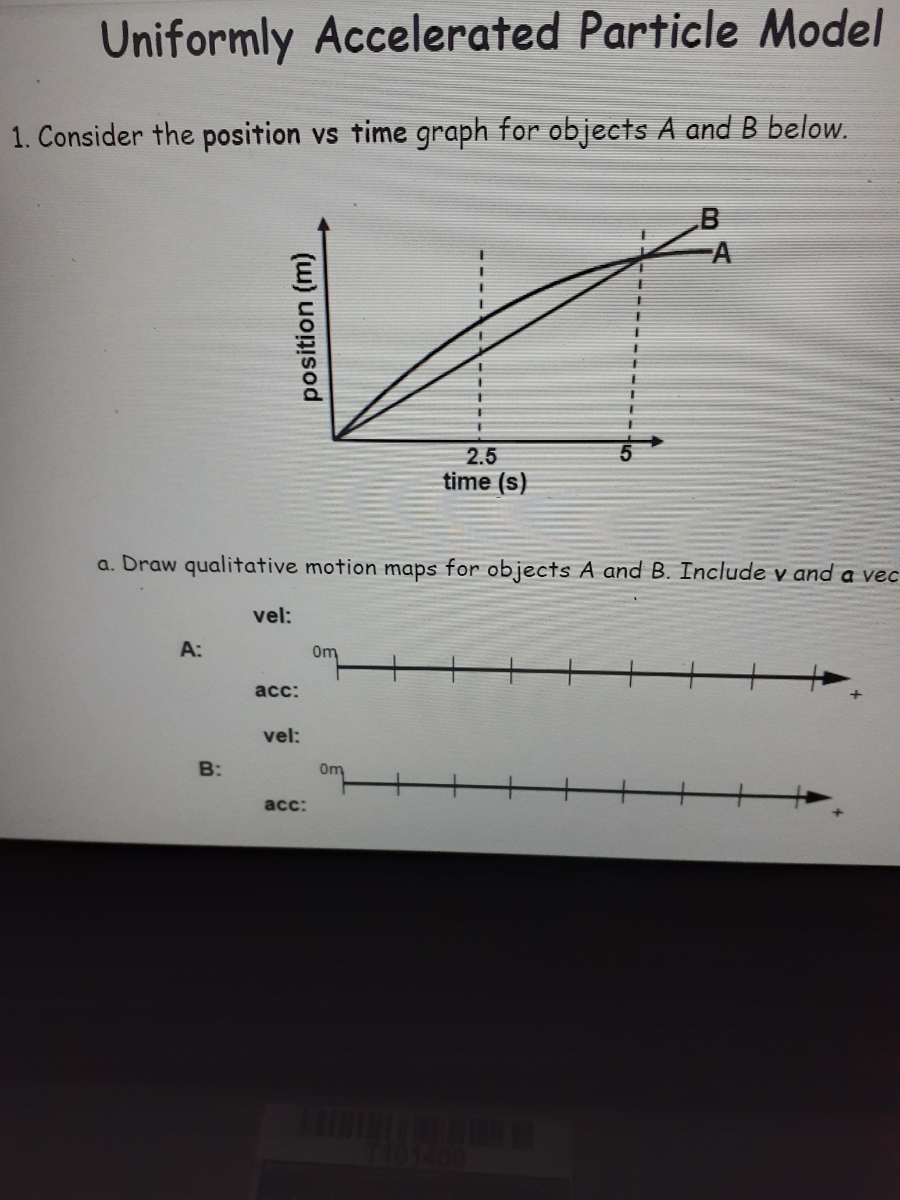
- Position vs. Time (d-t): This graph shows how an object’s location changes with time. It helps in analyzing the displacement and can indicate the velocity from the slope.
- Velocity vs. Time (v-t): Velocity-time graphs provide information about speed and acceleration. The slope of this graph gives acceleration, and the area under the curve gives displacement.
- Acceleration vs. Time (a-t): Acceleration-time curves illustrate how acceleration varies over time. The area under this graph provides the change in velocity.
👨🏫 Note: Pay attention to the units of measurement on the axes, as they can greatly influence your interpretation of the curves.
Analyzing Kinematic Curves
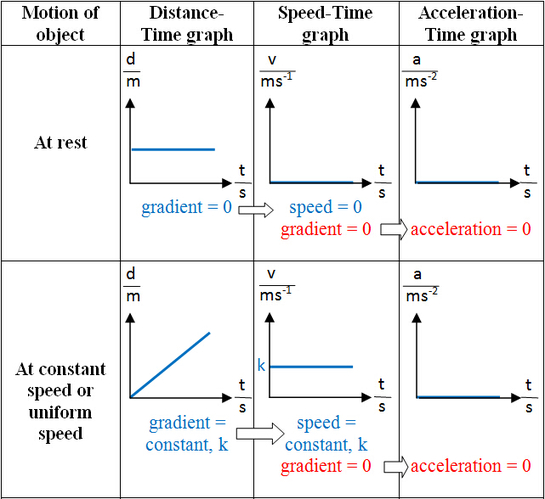
Position-Time Curves
| Slope of the Curve | Meaning |
|---|---|
| Zero Slope | No velocity, stationary object. |
| Positive Slope | Motion in the positive direction (e.g., moving forward). |
| Negative Slope | Motion in the negative direction (e.g., moving backward). |
| Curvature | Indicates acceleration or deceleration. |

Velocity-Time Curves

- Slope: The slope of a v-t curve equals acceleration (a).
- Area: The area under the v-t curve gives displacement (d).
🚲 Note: If an object’s velocity is constant, the v-t graph will be a straight line parallel to the time axis.
Acceleration-Time Curves

- Slope: Though less common, it indicates the rate of change in acceleration, known as jerk.
- Area: The area under the a-t curve provides the change in velocity (v).
Practical Examples and Exercises

Let's delve into practical examples of how to interpret these kinematic curves:
Example 1: Linear Motion

An object starts from rest and accelerates at a constant rate. Here's how we interpret this:
- The position-time curve would start at the origin (0,0) and curve upwards with a constant increasing slope.
- The velocity-time curve will be a straight line with a positive slope, indicating constant acceleration.
- The acceleration-time curve is a horizontal line representing constant acceleration.
Example 2: Circular Motion

For an object moving with uniform circular motion:
- The position-time curve is cyclical, showing a repeating pattern as the object returns to its initial position.
- The velocity-time curve would show constant magnitude but varying direction, potentially indicated by sine or cosine functions.
- The acceleration-time curve would reveal the centripetal acceleration, directed towards the center of the circle.
🔍 Note: Ensure to keep track of the object's direction when analyzing circular motion curves.
Advanced Concepts in Kinematics

Curves of Non-Uniform Motion

Non-uniform motion often involves changing acceleration, which can be quite complex:
- Position-Time: The curve might not follow a simple trend, with varying slopes showing fluctuating velocity.
- Velocity-Time: Here, the curve could have inflections points where acceleration changes.
- Acceleration-Time: The graph could display various peaks or troughs, representing changes in acceleration.
In-depth Analysis
To deepen your understanding, consider these additional points:
Application of Calculus in Kinematics
Calculus provides the mathematical tools for analyzing instantaneous rates of change in position, velocity, and acceleration:
- Derivative: The derivative of a function at any point gives the slope of the curve at that point, which in physics translates to velocity or acceleration.
- Integral: The integral of a function provides the area under the curve, useful for displacement or change in velocity.
📚 Note: A good grasp of calculus can significantly enhance your kinematic analysis skills.
Wrapping Up

This deep dive into kinematic curves has likely equipped you with a solid foundation to interpret, analyze, and understand the motion of objects. From the fundamental concepts of position, velocity, and acceleration graphs to applying calculus for a more nuanced understanding, you now have the tools to master motion analysis. Remember, practice with real-world examples will cement your understanding and make kinematic curves a second nature to interpret. Whether you're solving problems for academic purposes, preparing for physics competitions, or just indulging in the beauty of physical laws, these curves will continue to provide insights into the dynamics of the world around us.
What are the advantages of using graphs in kinematics?
+
Graphs provide a visual representation that can make it easier to understand and analyze motion. They allow for immediate comprehension of relationships between position, velocity, and acceleration, making it possible to quickly identify trends, patterns, and anomalies in an object’s movement.
How can I tell if an object is accelerating from its position-time graph?

+
Acceleration in a position-time graph is indicated by changes in the slope of the curve. If the slope is constant, the object is moving at a constant velocity; if the slope changes, the object is accelerating. An increasing slope means positive acceleration, and a decreasing slope means negative acceleration.
Can kinematic curves predict future motion?

+
While kinematic curves do not predict motion with absolute certainty, they can provide information about the current state of motion. If acceleration is constant, velocity can be predicted; if velocity is constant, future positions can be determined. However, for objects experiencing forces that change unpredictably, predictions would need more complex models.



