5 Simple Tricks for Writing Ionic Compound Formulas

Mastering the art of writing chemical formulas is essential for any student or enthusiast in the field of chemistry. While some might find it daunting, understanding ionic compound formulas can be made straightforward through a few simple tricks. In this comprehensive guide, we'll delve into the basics of ions, chemical formulas, and how to write ionic compounds easily.

Understanding Ions

Before jumping into formulas, let’s ensure we have a firm grasp on what ions are. Ions are atoms or molecules that have lost or gained electrons, resulting in a net electrical charge. Here’s what you need to know:

• Positive Ions (Cations): These are formed when an atom loses electrons.
• Negative Ions (Anions): These are created when atoms gain electrons.

The balancing of these charges is key to creating stable ionic compounds. Here's a simple way to remember which elements tend to lose or gain electrons:

• Metals generally lose electrons to become positively charged (e.g., Sodium becomes Na⁺).
• Non-metals often gain electrons, becoming negatively charged (e.g., Chlorine becomes Cl^-).

The Cross Over Method

Perhaps the most famous trick for writing ionic formulas is the crossover method. Here's how it works:

💡 Note: This method is particularly handy when dealing with ions that have a charge greater than one.

1. Identify Ions: Know the charges of the ions involved. For example, calcium (Ca²⁺) and chloride (Cl^-).
2. Cross the Charges: Cross over the numerical value of the charges. For CaCl, you cross the 2 from Ca²⁺ and the 1 from Cl^-.
3. Write the Formula: Ca now has 1 subscript, and Cl has 2. Therefore, the formula becomes CaCl₂.

This method ensures that the compound is electrically neutral, with the sum of positive and negative charges being zero.

Using Roman Numerals

For transition metals like iron, which can exhibit multiple oxidation states, Roman numerals are used to clarify the ion’s charge. Here’s an approach:

• Identify the Ion: Determine the oxidation state from the compound’s name or context. For instance, Fe(II) indicates iron is in a +2 state.
• Balance the Charges: Use the crossover method to balance the charges.

By doing this, writing formulas becomes more systematic, reducing the chances of errors.

The Simplification Trick

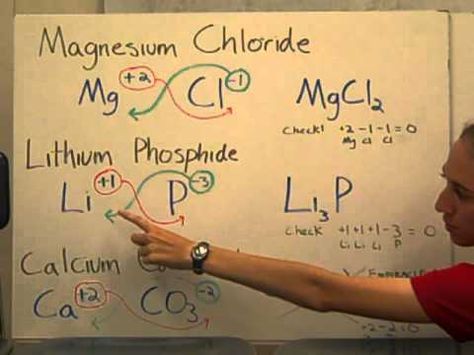
When dealing with larger ions, it might seem overwhelming to use the crossover method, but here’s a trick:

• Reduce to Smallest Units: After determining the formula, always reduce the subscripts to their simplest form.

For example, if you end up with Ca₂Cl₂, simplify it to CaCl, as it’s the same compound but with a more straightforward formula.

The Polyatomic Ion Shortcut

Polyatomic ions can be tricky due to their compound nature. Here’s how to manage them:

• Memorize Common Polyatomic Ions: Knowing ions like sulfate (SO₄^2-) or nitrate (NO₃^-) can save time.
• Treat as a Single Unit: When using the crossover method, consider the entire polyatomic ion as one unit, like (SO₄) instead of individual elements.

This approach simplifies the process significantly, especially when dealing with compounds like sodium sulfate (Na₂SO₄).

These simple tricks, when applied consistently, will make writing ionic compound formulas an intuitive and straightforward task. By understanding ions, using the crossover method, employing Roman numerals for clarity, simplifying where possible, and treating polyatomic ions as single units, you'll enhance your ability to write formulas with ease and confidence.

What are the most common polyatomic ions to memorize?

+

Here are some of the most common polyatomic ions to memorize:

• Sulfate (SO₄^2-)
• Nitrate (NO₃^-)
• Phosphate (PO₄^3-)
• Carbonate (CO₃^2-)
• Hydroxide (OH^-)

How do I know when to use Roman numerals in ionic formulas?

+

You should use Roman numerals when naming ionic compounds involving transition metals or metals that can have multiple oxidation states, like Iron (II) or Iron (III).

Can I simplify any ionic compound formula?

+

Yes, always simplify your formulas to the smallest integer ratio of elements. If your crossover method results in a formula with reducible subscripts, you should simplify it to avoid unnecessary complexity.