Zombie Math: Mastering Midpoint and Distance Formulas

In the ever-undead world of mathematics, where zombies roam the Euclidean plains, knowing how to navigate through this spooky landscape with precision is crucial. This article is dedicated to mastering the Midpoint and Distance formulas, which are fundamental in zombie survival scenarios as well as in regular geometry courses. Let's delve into these critical calculations, ensuring you can keep up with or escape from any mathematical zombie, or simply excel in your next exam!
Why Zombies Love Coordinates

Imagine a world where every zombie's movement can be tracked through a coordinate plane. Zombies, after all, are quite predictable in their shambling, making the use of coordinates not only educational but also highly practical for planning escape routes or setting up a stronghold. Here's how coordinates come into play:
- Navigation: Understanding where zombies are moving can help survivors plot safe paths.
- Analysis: Predicting zombie behavior based on past movement patterns.
- Survival: Knowing the midpoint between you and the zombie can be vital for strategic retreats or attacks.
Let's explore the essentials of the Midpoint and Distance formulas:
The Midpoint Formula
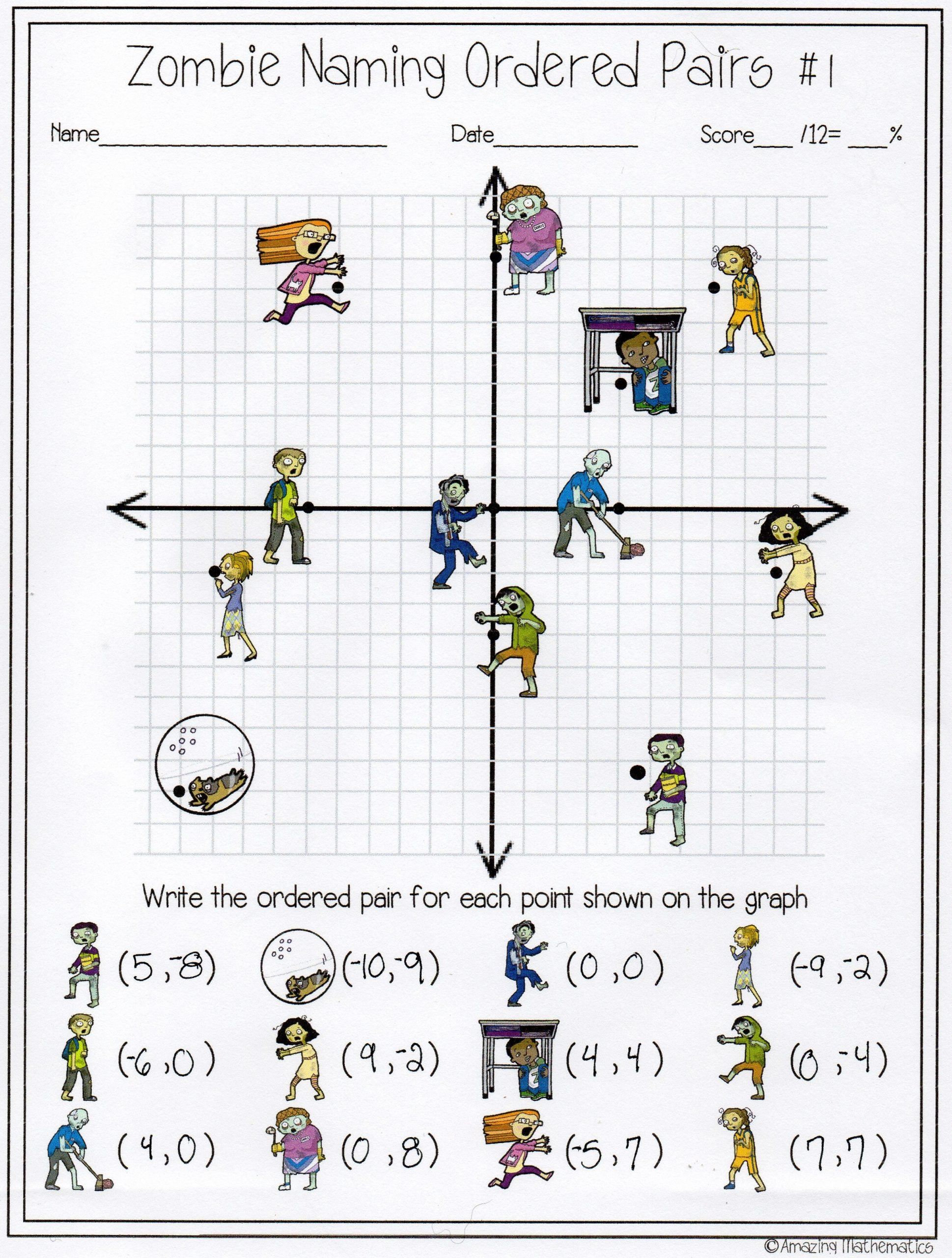
The midpoint formula calculates the exact center point between two given points on a coordinate grid. It's crucial in:
- Finding the middle ground in a zombie chase.
- Setting up ambushes or traps exactly halfway between your current position and where you expect zombies to pass through.
Here is the formula for finding the midpoint (M) between any two points (x1, y1) and (x2, y2):
M = ((x1 + x2)/2 , (y1 + y2)/2)
💡 Note: Remember, this formula works in any dimension, from 2D to nD, making it universal in your zombie survival kit!
The Distance Formula

Knowing how far away a zombie is can help determine if you have time to strategize or need to make a run for it. The distance formula, derived from the Pythagorean Theorem, allows us to calculate this distance directly. Here's how:
- Track how close a zombie is to your location or to another point of interest.
- Plan your movements with precision, understanding your physical reach and escape possibilities.
Here is the formula to calculate the distance (d) between two points (x1, y1) and (x2, y2):
d = sqrt((x2 - x1)² + (y2 - y1)²)
💡 Note: Remember to use the positive square root of the sum of squared differences to ensure a real-world, positive distance.
Real-World Zombie Math Applications

| Scenario | Formula | Application |
|---|---|---|
| Fleeing from a Zombie | Distance Formula | Calculate if you have enough time to reach safety or if a distraction is necessary. |
| Setting up a Safe Zone | Midpoint Formula | Determine the safest place to set up camp, equidistant from two known zombie hotspots. |
| Zombie Traps | Midpoint & Distance | Place traps at the midpoint between your location and common zombie paths to maximize effectiveness. |

To wrap up, mastering the Midpoint and Distance formulas is not only useful for surviving in a world of zombies but is also a fundamental part of geometry. Whether plotting an escape route or calculating the radius of your defensive perimeter, these formulas give you the strategic advantage. By understanding coordinates, predicting movement, and effectively calculating distances and midpoints, you'll find yourself better equipped to handle the undead or ace your next math test with zombie-like determination!
Why are coordinates important in zombie survival?
+
Coordinates allow survivors to map out zombie movements, plan escape routes, and set up strategic defenses, making the survival odds significantly better.
Can I use the midpoint formula for more than two points?

+
Yes, while it’s commonly used between two points, you can find the midpoint of a line segment or a set of points by averaging the coordinates of all points involved.
What’s the difference between using the Pythagorean Theorem and the Distance Formula?

+
The Distance Formula is essentially an application of the Pythagorean Theorem in two dimensions, making it specifically useful for calculating distances in a coordinate plane.