Inverse trigonometric functions, or arc functions, are a fundamental part of trigonometry, helping us solve for angles when we know the sides of a triangle. Whether you're preparing for an exam, working on an engineering problem, or simply solving a math puzzle, understanding how to tackle inverse trigonometric angles can be incredibly useful. Here are five essential tips to master these functions and solve for angles effectively:
Understand the Basics
Before you dive into complex problems, ensure you have a solid grasp of the basic principles of inverse trigonometric functions:
- Arcsin (sin⁻¹): This function returns the angle whose sine is a given number. The output is in the range [-π/2, π/2].
- Arccos (cos⁻¹): Returns the angle whose cosine is a given number, with the range [0, π].
- Arctan (tan⁻¹): Gives the angle whose tangent is a given number, ranging from [-π/2, π/2].
Remember that these functions are not just inverses; they have specific ranges that reflect the nature of trigonometric identities.
Recognize Quadrants
Inverse trigonometric functions generally give solutions within specific quadrants:
- Arcsin: Results in Quadrants I and IV.
- Arccos: Returns an angle in Quadrant I or II.
- Arctan: Returns solutions in Quadrants I and IV, unless you're dealing with arctan2 (which provides solutions in all quadrants).
📌 Note: Understanding the signs of functions in different quadrants helps in identifying which quadrant to look for the solution in.
Check for Multiple Solutions
Trigonometric equations often have multiple solutions. For instance, if you solve:
[ \sin(x) = \frac{1}{2} ]
You'll get:
[ x = \sin^{-1}\left(\frac{1}{2}\right) = \frac{\pi}{6} \text{ or } \frac{5\pi}{6} ]
Always consider the full range of angles that satisfy the given trigonometric function.
Use Identities and Properties
Leverage trigonometric identities to simplify or transform problems:
- Pythagorean identity: \sin^2(x) + \cos^2(x) = 1
- Sum and difference identities:
- \sin(a \pm b) = \sin(a)\cos(b) \pm \cos(a)\sin(b)
- \cos(a \pm b) = \cos(a)\cos(b) \mp \sin(a)\sin(b)
- Double angle identities:
- \sin(2x) = 2\sin(x)\cos(x)
- \cos(2x) = \cos^2(x) - \sin^2(x)
🛠 Note: Using identities can often reduce the complexity of the problem or provide an alternative route to the solution.
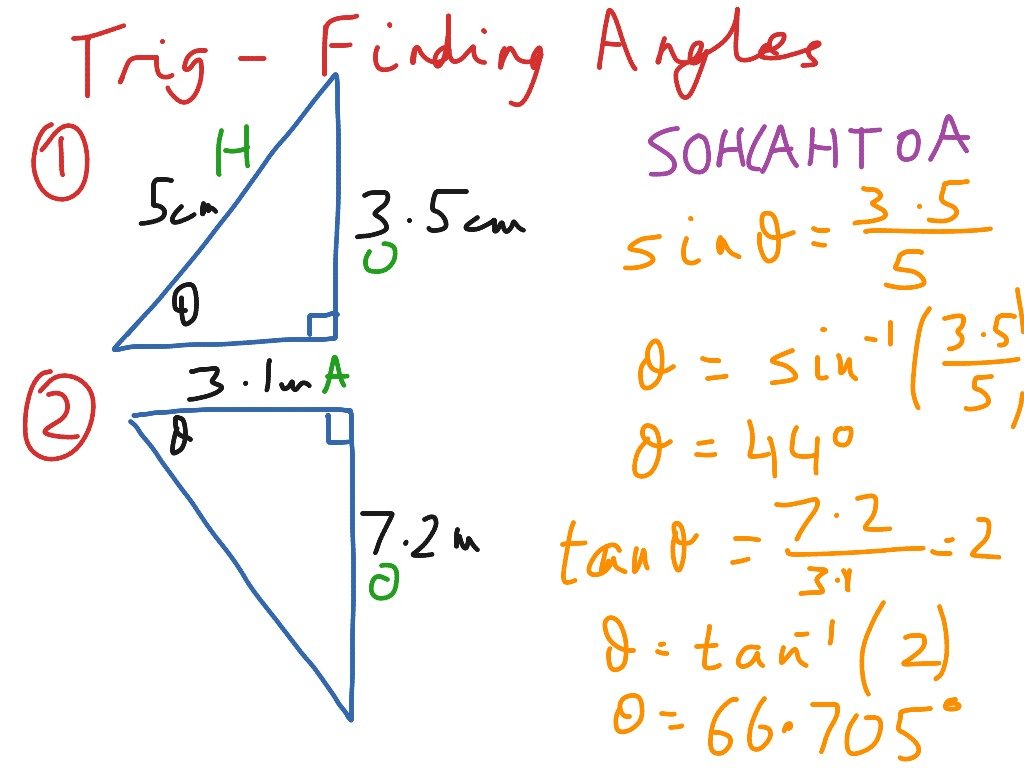
Practice with Real-world Applications
![Trig Identities Cheat Sheet [Solving Trigonometric Proofs], 48% Off](https://support.althea.net/assets/img/trig-identities-cheat-sheet-solving-trigonometric-proofs-48-off.jpeg "Trig Identities Cheat Sheet [Solving Trigonometric Proofs], 48% Off")
Applying inverse trigonometric functions in real-world scenarios helps solidify understanding:
| Scenario | Trig Function | Application |
|---|---|---|
| Finding angles in a right-angled triangle | sin⁻¹, cos⁻¹, tan⁻¹ | Calculating the height of a tree using the angle of elevation from the ground |
| Navigation and surveying | arccos | Finding bearings and distance on a plane |
| Voltage in AC circuits | arctangent | Determining phase shift between current and voltage |
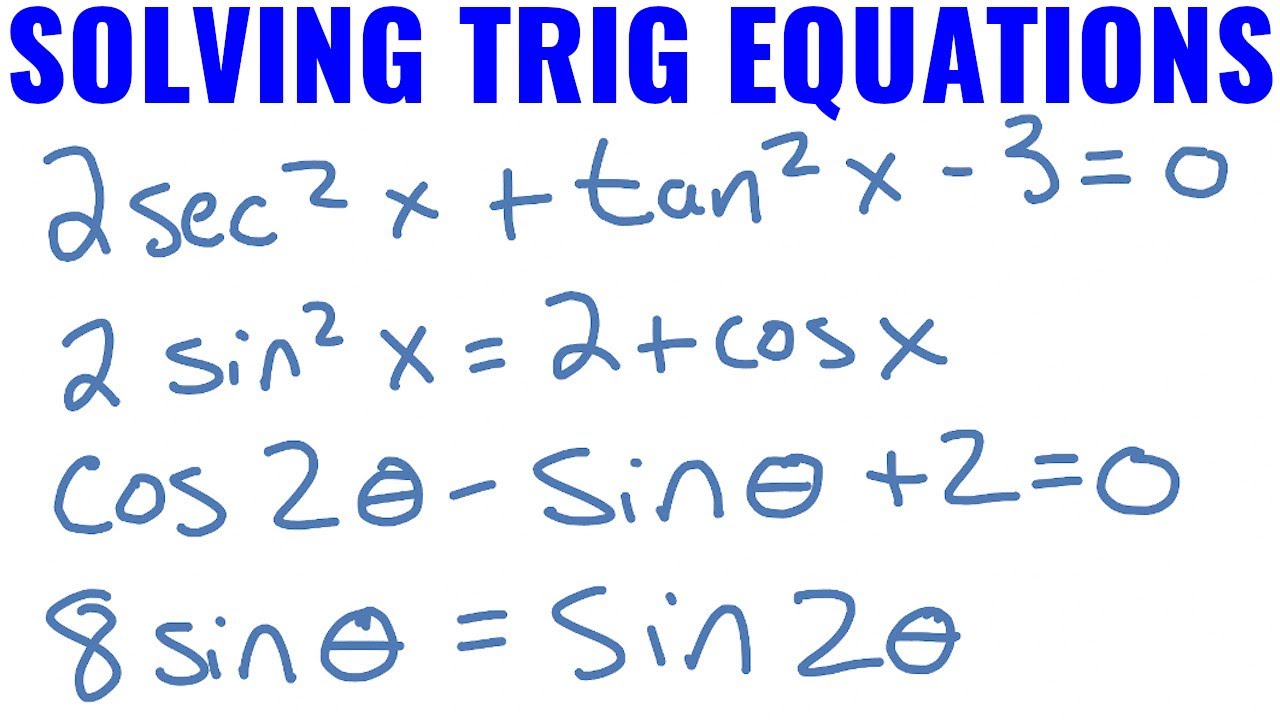
These applications can make the abstract concepts of trigonometry tangible and memorable.
In summary, solving inverse trigonometric functions effectively involves understanding the basics, recognizing the quadrants where solutions occur, checking for multiple solutions, using identities to simplify problems, and practicing with real-world scenarios. These strategies not only enhance your problem-solving skills but also make trigonometry an exciting part of mathematical inquiry. Whether for academic purposes or practical applications, mastering inverse trigonometric functions opens up a world of problem-solving possibilities.
What are the principal values for arcsin?
+
The principal values for arcsin, or sin⁻¹, range from -π/2 to π/2 (or -90° to 90°). Any angle outside this range will be equivalent to an angle within this range due to the periodicity of sine function.
Can arcsin ever yield angles outside its principal range?
+
Arcsin returns angles within its principal range by definition, but when solving trigonometric equations, you should consider additional solutions that correspond to the periodicity of the trigonometric functions.
Why do we need to consider quadrants when using inverse trigonometric functions?
+
Trigonometric functions are periodic, meaning they repeat their values. Considering quadrants helps identify which angle within one period of the function yields the given value. This is crucial for understanding the full set of solutions.
