5 Essential Tips for Mastering Dilations and Scale Factors

The transformation of shapes by expanding or shrinking them uniformly, known as dilation, is a fundamental concept in geometry. Whether you're studying for your next math exam or just enhancing your spatial intelligence, mastering dilations and scale factors can give you a competitive edge. Here are the five essential tips to help you ace this area of mathematics:
Understand the Concept of a Scale Factor

At the core of mastering dilations is the scale factor. This is the ratio by which every segment of a shape is enlarged or reduced. Here’s how to fully grasp this:
- Definition: The scale factor is either greater than 1 for enlargement or between 0 and 1 for reduction.
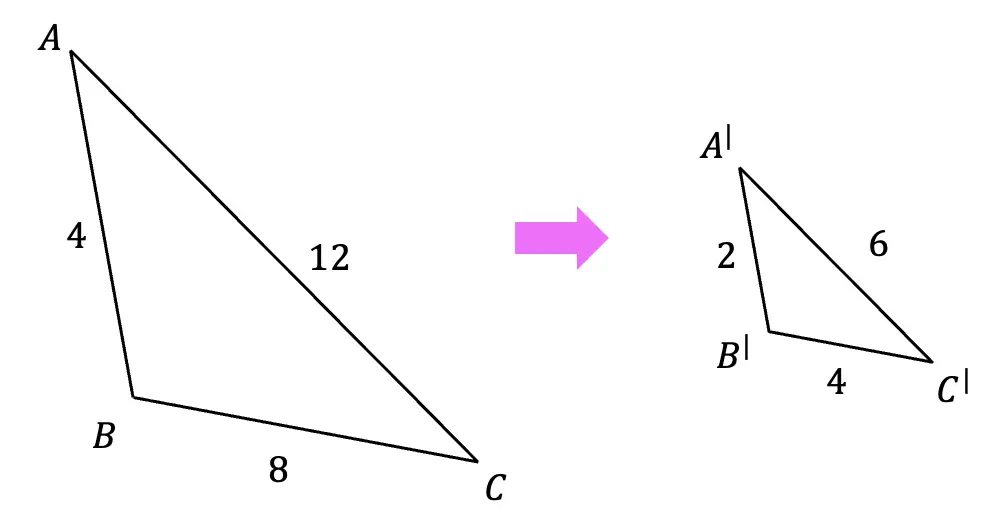
- Formula: The new length of a segment = Original length × Scale Factor.
- Example: If a triangle with sides measuring 3 cm, 4 cm, and 5 cm is dilated with a scale factor of 2, each side will become 6 cm, 8 cm, and 10 cm respectively.
Visualize Dilations in the Coordinate Plane
Using a coordinate plane to visualize dilations can simplify the process:
- Place the center of dilation, often denoted as “O,” at the origin (0, 0) for simplicity.
- Understand how each point on the original figure will move away from or towards the center of dilation.
- Calculate new coordinates for each point by multiplying the coordinates by the scale factor.
| Original Point (x, y) | Scale Factor | New Point (x', y') |
|---|---|---|
| (2, 3) | 2 | (4, 6) |
| (-1, 1) | 3 | (-3, 3) |

🔍 Note: When the center of dilation is not the origin, adjustments must be made to the coordinates to reflect the shift in the center point.
Use Proportions to Determine New Dimensions

Another strategy to master dilations involves understanding proportions:
- Set up a proportion to find new lengths. For example, if the original length is 6 cm and you want to find the new length when dilated with a scale factor of 1.5:
- The proportion will look like this: (\frac{6 \text{ cm}}{x \text{ cm}} = 1.5). Solving this, we find (x = 9 \text{ cm}).
Practice with Real-Life Applications

Dilations are not only theoretical; they have practical applications:
- Scale models of buildings or landscapes use dilation principles to ensure accuracy.
- Maps and blueprints rely on scale factors for accurate representation.
- Graphic design uses dilation to resize images while maintaining proportions.
By solving real-world problems, you not only reinforce your understanding but also appreciate the significance of dilations.
Examine Transformations in Different Settings

Understanding how dilations work in different environments can broaden your perspective:
- Observe dilations in art, where artists play with proportions to create visual effects.
- Analyze computer graphics, where transformations like dilations are used for zooming and resizing.
- Delve into physics or biology, where scaling laws often come into play, e.g., with the surface area to volume ratios.
Each setting offers unique challenges and solutions that enrich your understanding of dilations.
In closing, mastering dilations and scale factors hinges on understanding the core concepts, visualizing transformations, employing proportions, applying the knowledge to real-life scenarios, and exploring different contexts. These tips provide a comprehensive approach to not only understanding dilations but excelling in them. This knowledge not only benefits you in academic settings but also opens up a broader perspective on how transformations play a role in various fields, making you a well-rounded individual capable of applying mathematical principles to a wide array of problems.
What is the difference between enlargement and reduction in terms of dilation?

+
Enlargement happens when the scale factor is greater than 1, making the figure larger, while reduction occurs with a scale factor between 0 and 1, making the figure smaller.
How do you find the center of dilation if it is not given?

+
To find the center of dilation, connect corresponding points of the original and dilated figures with lines; the center will be where all these lines intersect.
Can dilations change the shape of the figure?

+
No, dilations maintain the shape of the figure, altering only the size. The angle measures stay the same, and parallel lines remain parallel.



