5 Essential Logarithms Concepts Explained

Logarithms, often viewed as one of the more abstract and challenging concepts in mathematics, play a pivotal role not just in advanced mathematical theory but also in various practical applications, from finance to engineering. In this post, we'll explore five fundamental concepts of logarithms that are crucial for understanding their utility and power in both theoretical and practical contexts.
1. The Definition and Basic Properties

Logarithms are the inverse operation of exponentiation. If you have an equation like (a^b = c), then (\log_a© = b). This means that if (a) raised to the power (b) equals (c), then the logarithm base (a) of (c) is (b). Here are some basic properties:
- Logarithm of a product: (\log_a(MN) = \log_a(M) + \log_a(N))
- Logarithm of a quotient: (\log_a\left(\frac{M}{N}\right) = \log_a(M) - \log_a(N))
- Logarithm of a power: (\log_a(M^n) = n \cdot \log_a(M))
- Change of Base Formula: (\log_a(b) = \frac{\log_c(b)}{\log_c(a)}), where (c) can be any base you prefer.
2. Natural Logarithms

The natural logarithm, denoted as ( \ln(x) ), uses the constant ( e \approx 2.71828 ) as its base. Here’s why they’re special:
- Natural logarithms appear naturally when solving problems involving exponential growth or decay, like population growth, radioactive decay, or compound interest.
- The derivative of ( \ln(x) ) is ( \frac{1}{x} ), which simplifies integration in calculus.
3. Logarithms and the Exponential Function

Understanding the relationship between exponential and logarithmic functions is crucial:
- The inverse nature means that ( e^{\ln(x)} = x ) and ( \ln(e^x) = x ).
- This relationship is pivotal in solving equations where an unknown is in an exponent.
📝 Note: Using this inverse relationship can transform complex equations into simpler forms that are easier to solve.
4. Logarithmic Scale

Logarithms are used to present data on a logarithmic scale which compresses huge ranges of values into manageable forms:
- This is useful in areas like seismology (Richter scale), sound intensity (decibels), pH levels, and astronomical distances (light-years).
- The table below shows how a logarithmic scale affects perception:
| Linear Increase | Logarithmic Scale (Base 10) | Example |
|---|---|---|
| 1 to 10 | log(1) to log(10) = 1 | From a quiet room to a normal conversation |
| 10 to 100 | log(10) to log(100) = 2 | From a conversation to a rock concert |

5. Applications in Real World

Logarithms have numerous real-world applications:
- Finance: Compound interest calculations.
- Engineering: Decibels in sound engineering, earthquake magnitude scales.
- Computing: Complexity analysis in algorithms where logarithmic time complexity indicates efficiency in handling large data sets.
In wrapping up our exploration of logarithms, we’ve covered their foundational definitions, the unique characteristics of natural logarithms, the interplay with exponential functions, how logarithmic scales transform our understanding of large data sets, and the wide range of their applications. Understanding these concepts not only enriches one’s knowledge of mathematics but also provides tools for problem-solving across various disciplines. The utility of logarithms lies in their ability to simplify complex calculations, interpret exponential growth, and scale data in a way that makes sense in real-world contexts. With this knowledge, you’re equipped to tackle problems from financial analysis to sound engineering with a newfound mathematical perspective.
What is the main difference between natural and common logarithms?

+
The primary difference is the base of the logarithm. Common logarithms use base 10, whereas natural logarithms use the base ( e ) (approximately 2.71828). Natural logarithms have specific properties that make them useful in natural growth and decay problems, and they have simpler calculus properties.
Why do we use logarithmic scales in some applications?
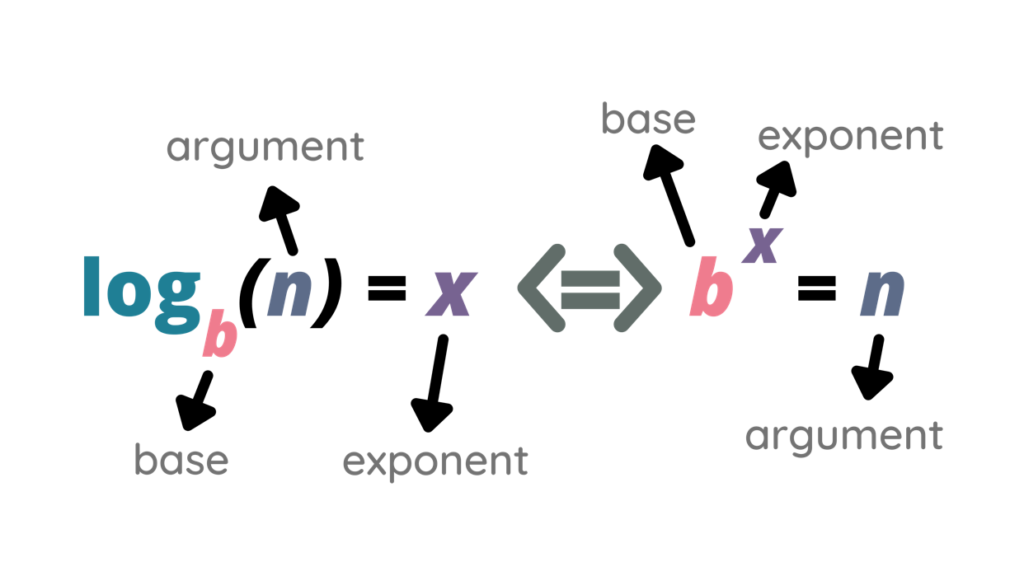
+
Logarithmic scales are used to manage and represent data that spans a large range of values. They compress this range, making it easier to analyze, compare, and visually interpret data that would otherwise appear too scattered on a linear scale.
How do logarithms help in simplifying exponential equations?

+
Logarithms provide a way to convert multiplicative and exponential relationships into additive ones, making it easier to solve complex equations. By taking the logarithm of both sides of an equation, you can simplify and linearize the problem for easier solution finding.
What is the significance of logarithms in the field of computing?

+
In computing, logarithmic functions often represent the efficiency of algorithms, particularly in searching and sorting techniques where the time complexity grows logarithmically with the size of the input, indicating a very efficient algorithm.



