Significant Figures Practice Worksheet: Answer Key Revealed

Understanding significant figures, often abbreviated as "sig figs," is crucial for precision and accuracy in scientific measurements, data analysis, and calculations. Whether you are a student, an engineer, or a scientist, knowing how to identify and use significant figures correctly is essential for effective communication in scientific communities.
The Basics of Significant Figures

Significant figures indicate the number of digits in a value that are known with some degree of reliability. Here’s a basic rundown:
- All non-zero digits are considered significant.
- Zeros between non-zero digits are significant.
- Leading zeros (to the left of the first non-zero digit) are not significant.
- Trailing zeros in a number with a decimal point are significant.
- Zeros in the last position following a decimal point are not significant unless a decimal point is present.
Detailed Examples and Practice

Let’s delve deeper into these rules with some examples:
Example 1: Counting Significant Figures

- 101.005 - 6 significant figures. (All non-zero digits and zeros between non-zero digits are significant.)
- 0.000235 - 3 significant figures. (Leading zeros are not significant; the rest are.)
- 1000 - Normally, this number has 1 significant figure, but…
📘 Note: A zero in the last position following a decimal point must be explicitly indicated by the placement of a decimal point.
Example 2: Scientific Notation

When numbers are written in scientific notation, all digits before the multiplication sign are significant:
- 2.500 × 10^3 - 4 significant figures.
- 3.0 × 10^-2 - 2 significant figures.
Example 3: Addition/Subtraction with Significant Figures

In these operations, your result should have the same number of decimal places as the number with the least decimal places:
- 34.5 + 6.352 = 40.85 (34.5 has only one decimal place, so the final answer has one decimal place)
Example 4: Multiplication/Division with Significant Figures

The result should have the same number of significant figures as the number in the calculation with the least significant figures:
- (6.23 × 0.34) / 2.1 = 1 (3 sig figs and 2 sig figs give an answer with 2 sig figs)
Worksheet Answer Key
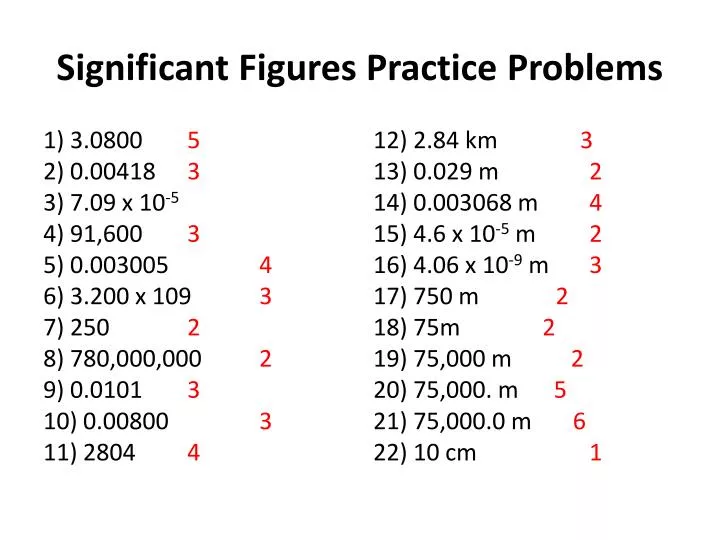
Here’s how you might handle a typical worksheet:
| Problem | Answer (with sig figs) |
|---|---|
| 3.06 + 4.1 | 7.2 |
| 100 - 14 | 86 |
| (2.50 × 3.4) / 8 | 1.1 |

How to Practice

Practicing with significant figures involves:
- Consistently identifying and counting significant figures in different types of numbers.
- Performing calculations and rounding according to the rules of significant figures.
- Using scientific notation to simplify working with very large or very small numbers.
Tips for Mastering Significant Figures

- Understand and apply the rules for significant figures in various scenarios.
- Always round off only at the end of calculations, not during intermediate steps.
- Remember that all measured or counted numbers are significant.
To wrap up, significant figures are more than just a measurement tool; they are a way to communicate precision and trust in scientific data. By practicing the rules of significant figures, you not only enhance your understanding of measurements but also ensure that your work stands up to the scrutiny of peers and scientific standards.
Why are significant figures important in scientific calculations?

+
Significant figures help scientists to communicate the precision of their measurements or calculations. They indicate how much of the number is known with certainty and how much is an estimate, thus maintaining the accuracy of scientific data.
How do you determine if a zero is significant?

+
Zeros are significant in the following cases: between non-zero digits, at the end of a number with a decimal point, and when explicitly indicated in scientific notation. Leading zeros are never significant.
Can I use an online calculator for significant figures?

+
Yes, many online tools exist that can help with significant figures. However, understanding and manually practicing with these rules is invaluable for grasping the underlying principles.